Leveraging ASIC AI Chips for Homomorphic Encryption

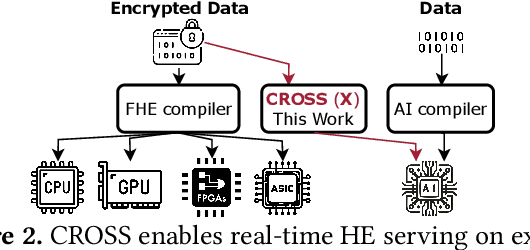
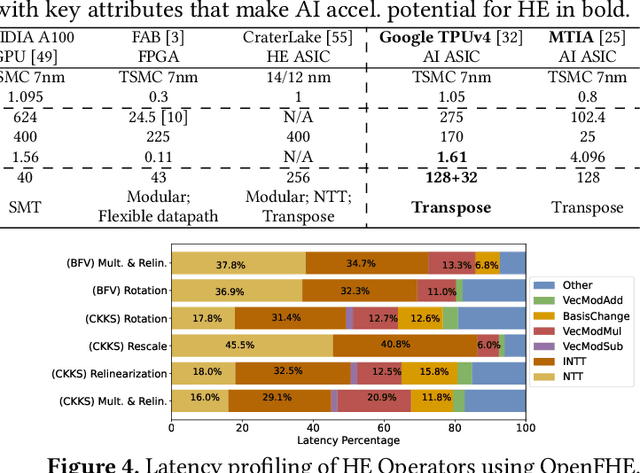
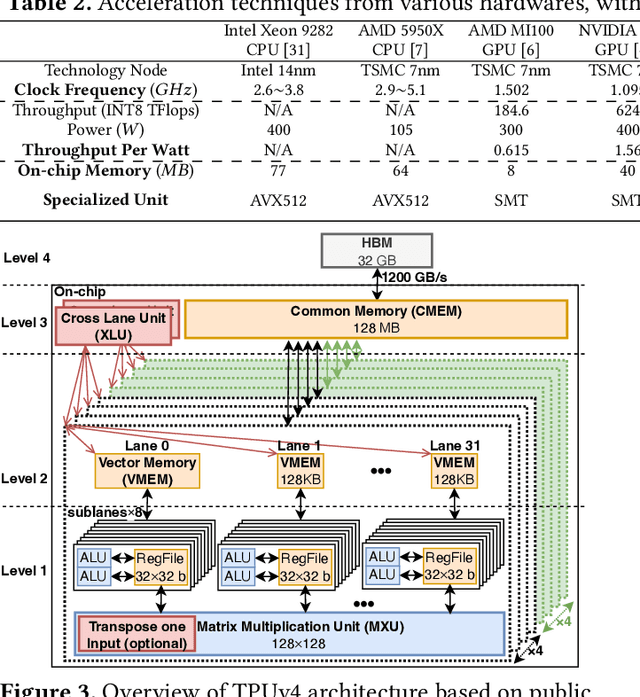
Cloud-based services are making the outsourcing of sensitive client data increasingly common. Although homomorphic encryption (HE) offers strong privacy guarantee, it requires substantially more resources than computing on plaintext, often leading to unacceptably large latencies in getting the results. HE accelerators have emerged to mitigate this latency issue, but with the high cost of ASICs. In this paper we show that HE primitives can be converted to AI operators and accelerated on existing ASIC AI accelerators, like TPUs, which are already widely deployed in the cloud. Adapting such accelerators for HE requires (1) supporting modular multiplication, (2) high-precision arithmetic in software, and (3) efficient mapping on matrix engines. We introduce the CROSS compiler (1) to adopt Barrett reduction to provide modular reduction support using multiplier and adder, (2) Basis Aligned Transformation (BAT) to convert high-precision multiplication as low-precision matrix-vector multiplication, (3) Matrix Aligned Transformation (MAT) to covert vectorized modular operation with reduction into matrix multiplication that can be efficiently processed on 2D spatial matrix engine. Our evaluation of CROSS on a Google TPUv4 demonstrates significant performance improvements, with up to 161x and 5x speedup compared to the previous work on many-core CPUs and V100. The kernel-level codes are open-sourced at https://github.com/google/jaxite.git.

A Multimodal Dataset for Enhancing Industrial Task Monitoring and Engagement Prediction

Detecting and interpreting operator actions, engagement, and object interactions in dynamic industrial workflows remains a significant challenge in human-robot collaboration research, especially within complex, real-world environments. Traditional unimodal methods often fall short of capturing the intricacies of these unstructured industrial settings. To address this gap, we present a novel Multimodal Industrial Activity Monitoring (MIAM) dataset that captures realistic assembly and disassembly tasks, facilitating the evaluation of key meta-tasks such as action localization, object interaction, and engagement prediction. The dataset comprises multi-view RGB, depth, and Inertial Measurement Unit (IMU) data collected from 22 sessions, amounting to 290 minutes of untrimmed video, annotated in detail for task performance and operator behavior. Its distinctiveness lies in the integration of multiple data modalities and its emphasis on real-world, untrimmed industrial workflows-key for advancing research in human-robot collaboration and operator monitoring. Additionally, we propose a multimodal network that fuses RGB frames, IMU data, and skeleton sequences to predict engagement levels during industrial tasks. Our approach improves the accuracy of recognizing engagement states, providing a robust solution for monitoring operator performance in dynamic industrial environments. The dataset and code can be accessed from https://github.com/navalkishoremehta95/MIAM/.

Optimizing Multitask Industrial Processes with Predictive Action Guidance

Monitoring complex assembly processes is critical for maintaining productivity and ensuring compliance with assembly standards. However, variability in human actions and subjective task preferences complicate accurate task anticipation and guidance. To address these challenges, we introduce the Multi-Modal Transformer Fusion and Recurrent Units (MMTFRU) Network for egocentric activity anticipation, utilizing multimodal fusion to improve prediction accuracy. Integrated with the Operator Action Monitoring Unit (OAMU), the system provides proactive operator guidance, preventing deviations in the assembly process. OAMU employs two strategies: (1) Top-5 MMTF-RU predictions, combined with a reference graph and an action dictionary, for next-step recommendations; and (2) Top-1 MMTF-RU predictions, integrated with a reference graph, for detecting sequence deviations and predicting anomaly scores via an entropy-informed confidence mechanism. We also introduce Time-Weighted Sequence Accuracy (TWSA) to evaluate operator efficiency and ensure timely task completion. Our approach is validated on the industrial Meccano dataset and the largescale EPIC-Kitchens-55 dataset, demonstrating its effectiveness in dynamic environments.

Identifying Money Laundering Subgraphs on the Blockchain

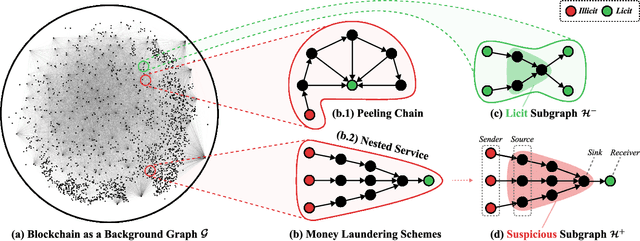
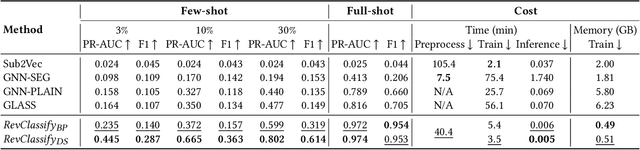
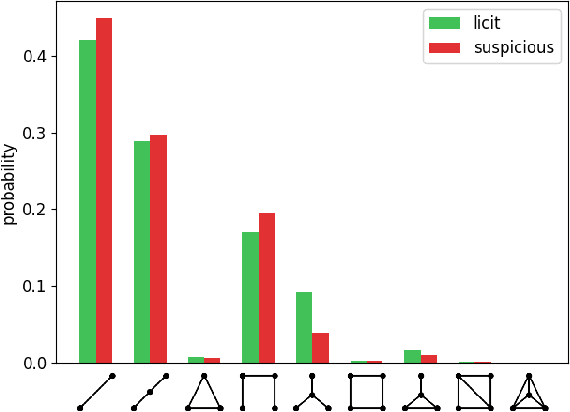
Anti-Money Laundering (AML) involves the identification of money laundering crimes in financial activities, such as cryptocurrency transactions. Recent studies advanced AML through the lens of graph-based machine learning, modeling the web of financial transactions as a graph and developing graph methods to identify suspicious activities. For instance, a recent effort on opensourcing datasets and benchmarks, Elliptic2, treats a set of Bitcoin addresses, considered to be controlled by the same entity, as a graph node and transactions among entities as graph edges. This modeling reveals the "shape" of a money laundering scheme - a subgraph on the blockchain. Despite the attractive subgraph classification results benchmarked by the paper, competitive methods remain expensive to apply due to the massive size of the graph; moreover, existing methods require candidate subgraphs as inputs which may not be available in practice. In this work, we introduce RevTrack, a graph-based framework that enables large-scale AML analysis with a lower cost and a higher accuracy. The key idea is to track the initial senders and the final receivers of funds; these entities offer a strong indication of the nature (licit vs. suspicious) of their respective subgraph. Based on this framework, we propose RevClassify, which is a neural network model for subgraph classification. Additionally, we address the practical problem where subgraph candidates are not given, by proposing RevFilter. This method identifies new suspicious subgraphs by iteratively filtering licit transactions, using RevClassify. Benchmarking these methods on Elliptic2, a new standard for AML, we show that RevClassify outperforms state-of-the-art subgraph classification techniques in both cost and accuracy. Furthermore, we demonstrate the effectiveness of RevFilter in discovering new suspicious subgraphs, confirming its utility for practical AML.

The Shape of Money Laundering: Subgraph Representation Learning on the Blockchain with the Elliptic2 Dataset

Subgraph representation learning is a technique for analyzing local structures (or shapes) within complex networks. Enabled by recent developments in scalable Graph Neural Networks (GNNs), this approach encodes relational information at a subgroup level (multiple connected nodes) rather than at a node level of abstraction. We posit that certain domain applications, such as anti-money laundering (AML), are inherently subgraph problems and mainstream graph techniques have been operating at a suboptimal level of abstraction. This is due in part to the scarcity of annotated datasets of real-world size and complexity, as well as the lack of software tools for managing subgraph GNN workflows at scale. To enable work in fundamental algorithms as well as domain applications in AML and beyond, we introduce Elliptic2, a large graph dataset containing 122K labeled subgraphs of Bitcoin clusters within a background graph consisting of 49M node clusters and 196M edge transactions. The dataset provides subgraphs known to be linked to illicit activity for learning the set of "shapes" that money laundering exhibits in cryptocurrency and accurately classifying new criminal activity. Along with the dataset we share our graph techniques, software tooling, promising early experimental results, and new domain insights already gleaned from this approach. Taken together, we find immediate practical value in this approach and the potential for a new standard in anti-money laundering and forensic analytics in cryptocurrencies and other financial networks.

Inferring physical laws by artificial intelligence based causal models

The advances in Artificial Intelligence (AI) and Machine Learning (ML) have opened up many avenues for scientific research, and are adding new dimensions to the process of knowledge creation. However, even the most powerful and versatile of ML applications till date are primarily in the domain of analysis of associations and boil down to complex data fitting. Judea Pearl has pointed out that Artificial General Intelligence must involve interventions involving the acts of doing and imagining. Any machine assisted scientific discovery thus must include casual analysis and interventions. In this context, we propose a causal learning model of physical principles, which not only recognizes correlations but also brings out casual relationships. We use the principles of causal inference and interventions to study the cause-and-effect relationships in the context of some well-known physical phenomena. We show that this technique can not only figure out associations among data, but is also able to correctly ascertain the cause-and-effect relations amongst the variables, thereby strengthening (or weakening) our confidence in the proposed model of the underlying physical process.