Quantum Policy Gradient in Reproducing Kernel Hilbert Space

Parametrised quantum circuits offer expressive and data-efficient representations for machine learning. Due to quantum states residing in a high-dimensional Hilbert space, parametrised quantum circuits have a natural interpretation in terms of kernel methods. The representation of quantum circuits in terms of quantum kernels has been studied widely in quantum supervised learning, but has been overlooked in the context of quantum reinforcement learning. This paper proposes parametric and non-parametric policy gradient and actor-critic algorithms with quantum kernel policies in quantum environments. This approach, implemented with both numerical and analytical quantum policy gradient techniques, allows exploiting the many advantages of kernel methods, including available analytic forms for the gradient of the policy and tunable expressiveness. The proposed approach is suitable for vector-valued action spaces and each of the formulations demonstrates a quadratic reduction in query complexity compared to their classical counterparts. Two actor-critic algorithms, one based on stochastic policy gradient and one based on deterministic policy gradient (comparable to the popular DDPG algorithm), demonstrate additional query complexity reductions compared to quantum policy gradient algorithms under favourable conditions.

A quantum tug of war between randomness and symmetries on homogeneous spaces

We explore the interplay between symmetry and randomness in quantum information. Adopting a geometric approach, we consider states as $H$-equivalent if related by a symmetry transformation characterized by the group $H$. We then introduce the Haar measure on the homogeneous space $\mathbb{U}/H$, characterizing true randomness for $H$-equivalent systems. While this mathematical machinery is well-studied by mathematicians, it has seen limited application in quantum information: we believe our work to be the first instance of utilizing homogeneous spaces to characterize symmetry in quantum information. This is followed by a discussion of approximations of true randomness, commencing with $t$-wise independent approximations and defining $t$-designs on $\mathbb{U}/H$ and $H$-equivalent states. Transitioning further, we explore pseudorandomness, defining pseudorandom unitaries and states within homogeneous spaces. Finally, as a practical demonstration of our findings, we study the expressibility of quantum machine learning ansatze in homogeneous spaces. Our work provides a fresh perspective on the relationship between randomness and symmetry in the quantum world.

Inferring physical laws by artificial intelligence based causal models

The advances in Artificial Intelligence (AI) and Machine Learning (ML) have opened up many avenues for scientific research, and are adding new dimensions to the process of knowledge creation. However, even the most powerful and versatile of ML applications till date are primarily in the domain of analysis of associations and boil down to complex data fitting. Judea Pearl has pointed out that Artificial General Intelligence must involve interventions involving the acts of doing and imagining. Any machine assisted scientific discovery thus must include casual analysis and interventions. In this context, we propose a causal learning model of physical principles, which not only recognizes correlations but also brings out casual relationships. We use the principles of causal inference and interventions to study the cause-and-effect relationships in the context of some well-known physical phenomena. We show that this technique can not only figure out associations among data, but is also able to correctly ascertain the cause-and-effect relations amongst the variables, thereby strengthening (or weakening) our confidence in the proposed model of the underlying physical process.

NISQ Algorithm for Semidefinite Programming

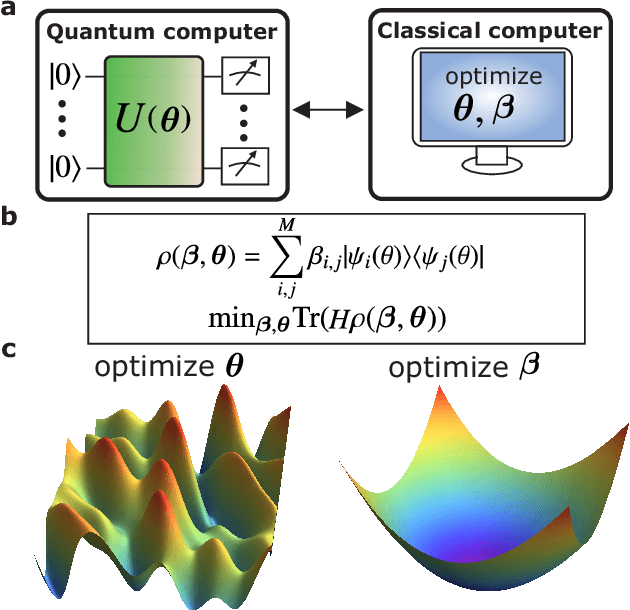
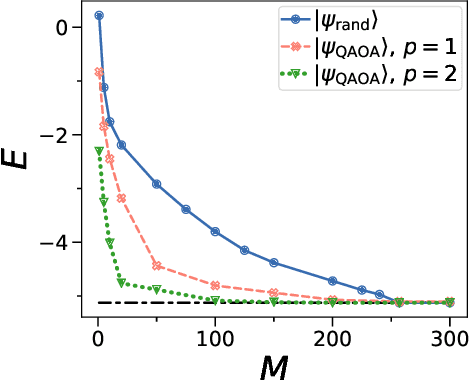
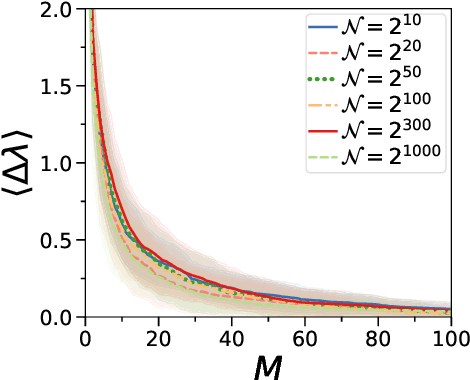
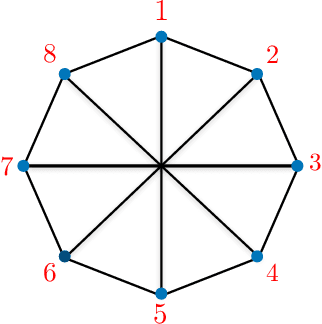
Semidefinite Programming (SDP) is a class of convex optimization programs with vast applications in control theory, quantum information, combinatorial optimization and operational research. Noisy intermediate-scale quantum (NISQ) algorithms aim to make an efficient use of the current generation of quantum hardware. However, optimizing variational quantum algorithms is a challenge as it is an NP-hard problem that in general requires an exponential time to solve and can contain many far from optimal local minima. Here, we present a current term NISQ algorithm for SDP. The classical optimization program of our NISQ solver is another SDP over a smaller dimensional ansatz space. We harness the SDP based formulation of the Hamiltonian ground state problem to design a NISQ eigensolver. Unlike variational quantum eigensolvers, the classical optimization program of our eigensolver is convex, can be solved in polynomial time with the number of ansatz parameters and every local minimum is a global minimum. Further, we demonstrate the potential of our NISQ SDP solver by finding the largest eigenvalue of up to $2^{1000}$ dimensional matrices and solving graph problems related to quantum contextuality. We also discuss NISQ algorithms for rank-constrained SDPs. Our work extends the application of NISQ computers onto one of the most successful algorithmic frameworks of the past few decades.

Capacity and quantum geometry of parametrized quantum circuits

To harness the potential of noisy intermediate-scale quantum devices, it is paramount to find the best type of circuits to run hybrid quantum-classical algorithms. Key candidates are parametrized quantum circuits that can be effectively implemented on current devices. Here, we evaluate the capacity and trainability of these circuits using the geometric structure of the parameter space via the effective quantum dimension, which reveals the expressive power of circuits in general as well as of particular initialization strategies. We assess the representation power of various popular circuit types and find striking differences depending on the type of entangling gates used. Particular circuits are characterized by scaling laws in their expressiveness. We identify a transition in the quantum geometry of the parameter space, which leads to a decay of the quantum natural gradient for deep circuits. For shallow circuits, the quantum natural gradient can be orders of magnitude larger in value compared to the regular gradient; however, both of them can suffer from vanishing gradients. By tuning a fixed set of circuit parameters to randomized ones, we find a region where the circuit is expressive, but does not suffer from barren plateaus, hinting at a good way to initialize circuits. Our results enhance the understanding of parametrized quantum circuits for improving variational quantum algorithms.

Noisy intermediate-scale quantum (NISQ) algorithms

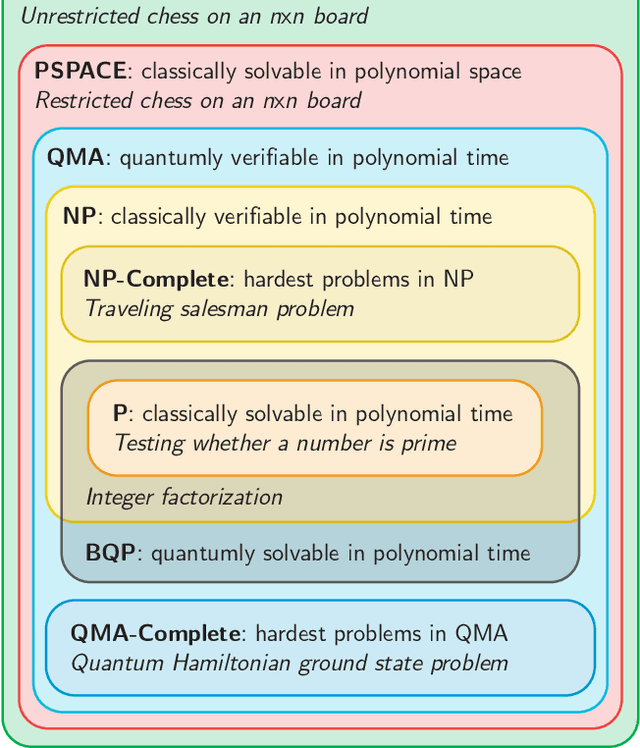
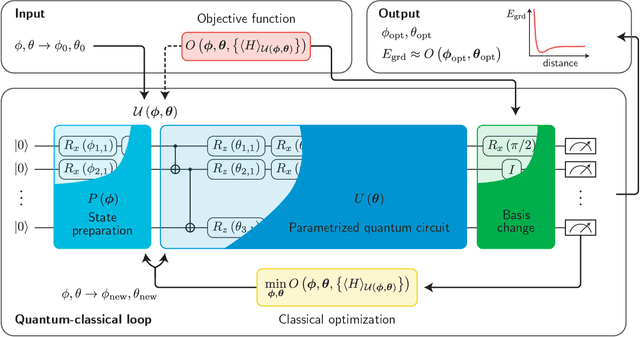
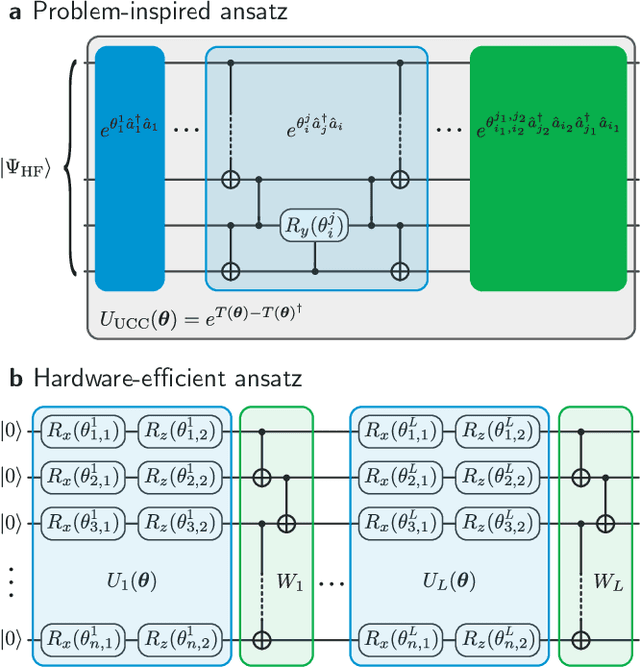
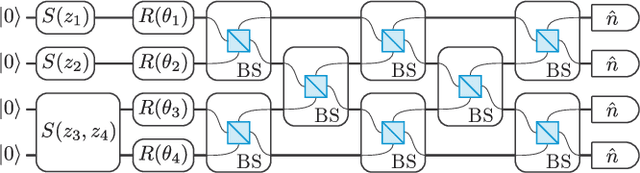
A universal fault-tolerant quantum computer that can solve efficiently problems such as integer factorization and unstructured database search requires millions of qubits with low error rates and long coherence times. While the experimental advancement towards realizing such devices will potentially take decades of research, noisy intermediate-scale quantum (NISQ) computers already exist. These computers are composed of hundreds of noisy qubits, i.e. qubits that are not error-corrected, and therefore perform imperfect operations in a limited coherence time. In the search for quantum advantage with these devices, algorithms have been proposed for applications in various disciplines spanning physics, machine learning, quantum chemistry and combinatorial optimization. The goal of such algorithms is to leverage the limited available resources to perform classically challenging tasks. In this review, we provide a thorough summary of NISQ computational paradigms and algorithms. We discuss the key structure of these algorithms, their limitations, and advantages. We additionally provide a comprehensive overview of various benchmarking and software tools useful for programming and testing NISQ devices.