Classical Shadows with Improved Median-of-Means Estimation

The classical shadows protocol, introduced by Huang et al. [Nat. Phys. 16, 1050 (2020)], makes use of the median-of-means (MoM) estimator to efficiently estimate the expectation values of $M$ observables with failure probability $\delta$ using only $\mathcal{O}(\log(M/\delta))$ measurements. In their analysis, Huang et al. used loose constants in their asymptotic performance bounds for simplicity. However, the specific values of these constants can significantly affect the number of shots used in practical implementations. To address this, we studied a modified MoM estimator proposed by Minsker [PMLR 195, 5925 (2023)] that uses optimal constants and involves a U-statistic over the data set. For efficient estimation, we implemented two types of incomplete U-statistics estimators, the first based on random sampling and the second based on cyclically permuted sampling. We compared the performance of the original and modified estimators when used with the classical shadows protocol with single-qubit Clifford unitaries (Pauli measurements) for an Ising spin chain, and global Clifford unitaries (Clifford measurements) for the Greenberger-Horne-Zeilinger (GHZ) state. While the original estimator outperformed the modified estimators for Pauli measurements, the modified estimators showed improved performance over the original estimator for Clifford measurements. Our findings highlight the importance of tailoring estimators to specific measurement settings to optimize the performance of the classical shadows protocol in practical applications.

A quantum tug of war between randomness and symmetries on homogeneous spaces

We explore the interplay between symmetry and randomness in quantum information. Adopting a geometric approach, we consider states as $H$-equivalent if related by a symmetry transformation characterized by the group $H$. We then introduce the Haar measure on the homogeneous space $\mathbb{U}/H$, characterizing true randomness for $H$-equivalent systems. While this mathematical machinery is well-studied by mathematicians, it has seen limited application in quantum information: we believe our work to be the first instance of utilizing homogeneous spaces to characterize symmetry in quantum information. This is followed by a discussion of approximations of true randomness, commencing with $t$-wise independent approximations and defining $t$-designs on $\mathbb{U}/H$ and $H$-equivalent states. Transitioning further, we explore pseudorandomness, defining pseudorandom unitaries and states within homogeneous spaces. Finally, as a practical demonstration of our findings, we study the expressibility of quantum machine learning ansatze in homogeneous spaces. Our work provides a fresh perspective on the relationship between randomness and symmetry in the quantum world.

Effects of quantum resources on the statistical complexity of quantum circuits

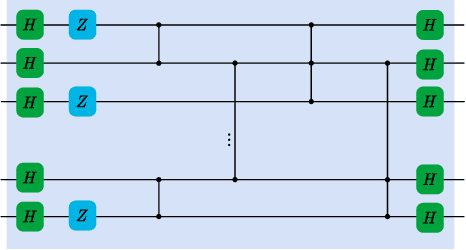
We investigate how the addition of quantum resources changes the statistical complexity of quantum circuits by utilizing the framework of quantum resource theories. Measures of statistical complexity that we consider include the Rademacher complexity and the Gaussian complexity, which are well-known measures in computational learning theory that quantify the richness of classes of real-valued functions. We derive bounds for the statistical complexities of quantum circuits that have limited access to certain resources and apply our results to two special cases: (1) stabilizer circuits that are supplemented with a limited number of T gates and (2) instantaneous quantum polynomial-time Clifford circuits that are supplemented with a limited number of CCZ gates. We show that the increase in the statistical complexity of a quantum circuit when an additional quantum channel is added to it is upper bounded by the free robustness of the added channel. Finally, we derive bounds for the generalization error associated with learning from training data arising from quantum circuits.

On the statistical complexity of quantum circuits

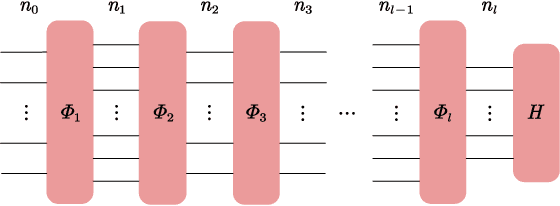
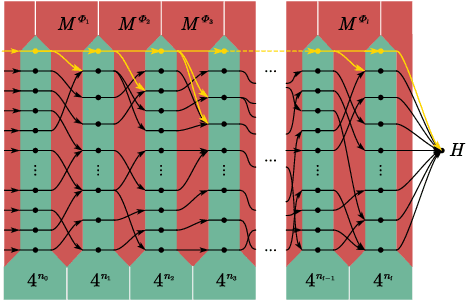
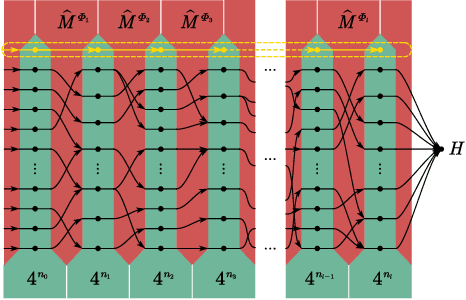
In theoretical machine learning, the statistical complexity is a notion that measures the richness of a hypothesis space. In this work, we apply a particular measure of statistical complexity, namely the Rademacher complexity, to the quantum circuit model in quantum computation and study how the statistical complexity depends on various quantum circuit parameters. In particular, we investigate the dependence of the statistical complexity on the resources, depth, width, and the number of input and output registers of a quantum circuit. To study how the statistical complexity scales with resources in the circuit, we introduce a resource measure of magic based on the $(p,q)$ group norm, which quantifies the amount of magic in the quantum channels associated with the circuit. These dependencies are investigated in the following two settings: (i) where the entire quantum circuit is treated as a single quantum channel, and (ii) where each layer of the quantum circuit is treated as a separate quantum channel. The bounds we obtain can be used to constrain the capacity of quantum neural networks in terms of their depths and widths as well as the resources in the network.

Classical Shadows with Noise

The classical shadows protocol, recently introduced by Huang, Keung, and Preskill [Nat. Phys. 16, 1050 (2020)], is a hybrid quantum-classical protocol that is used to predict target functions of an unknown quantum state. Unlike full quantum state tomography, the protocol requires only a few quantum measurements to make many predictions with a high success probability, and is therefore more amenable to implementation on near-term quantum hardware. In this paper, we study the effects of noise on the classical shadows protocol. In particular, we consider the scenario in which the quantum circuits involved in the protocol are subject to various known noise channels and derive an analytical upper bound for the sample complexity in terms of a generalized shadow norm for both local and global noise. Additionally, by modifying the classical post-processing step of the noiseless protocol, we define an estimator that remains unbiased in the presence of noise. As applications, we show that our results can be used to prove rigorous sample complexity upper bounds in the cases of depolarizing noise and amplitude damping.