Classical Shadows with Improved Median-of-Means Estimation

The classical shadows protocol, introduced by Huang et al. [Nat. Phys. 16, 1050 (2020)], makes use of the median-of-means (MoM) estimator to efficiently estimate the expectation values of $M$ observables with failure probability $\delta$ using only $\mathcal{O}(\log(M/\delta))$ measurements. In their analysis, Huang et al. used loose constants in their asymptotic performance bounds for simplicity. However, the specific values of these constants can significantly affect the number of shots used in practical implementations. To address this, we studied a modified MoM estimator proposed by Minsker [PMLR 195, 5925 (2023)] that uses optimal constants and involves a U-statistic over the data set. For efficient estimation, we implemented two types of incomplete U-statistics estimators, the first based on random sampling and the second based on cyclically permuted sampling. We compared the performance of the original and modified estimators when used with the classical shadows protocol with single-qubit Clifford unitaries (Pauli measurements) for an Ising spin chain, and global Clifford unitaries (Clifford measurements) for the Greenberger-Horne-Zeilinger (GHZ) state. While the original estimator outperformed the modified estimators for Pauli measurements, the modified estimators showed improved performance over the original estimator for Clifford measurements. Our findings highlight the importance of tailoring estimators to specific measurement settings to optimize the performance of the classical shadows protocol in practical applications.

QROSS: QUBO Relaxation Parameter Optimisation via Learning Solver Surrogates

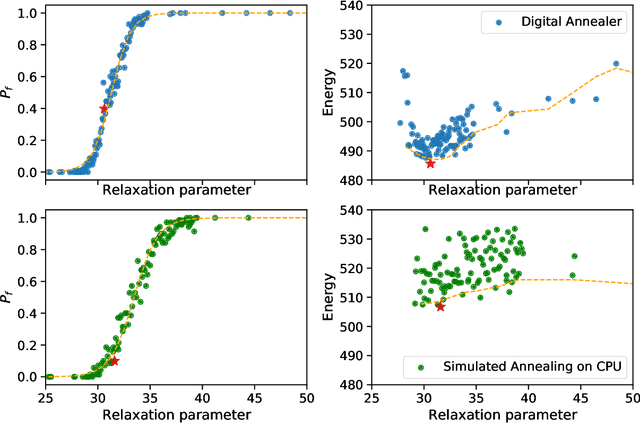
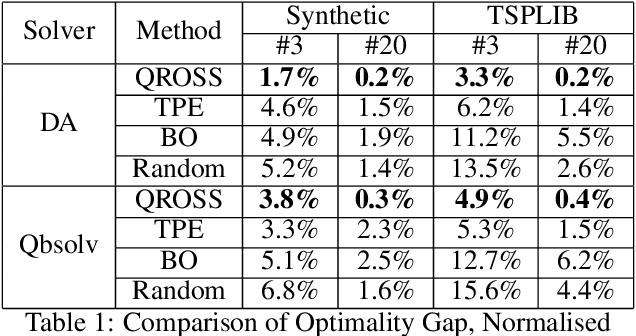
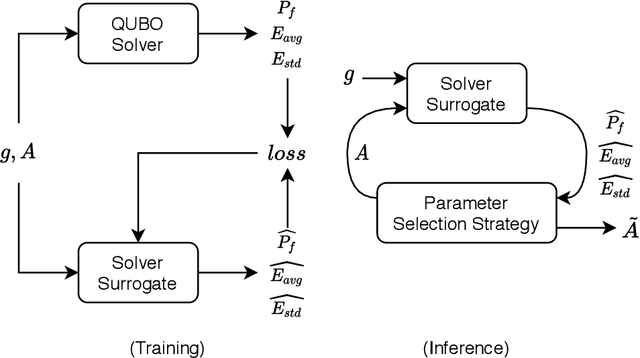
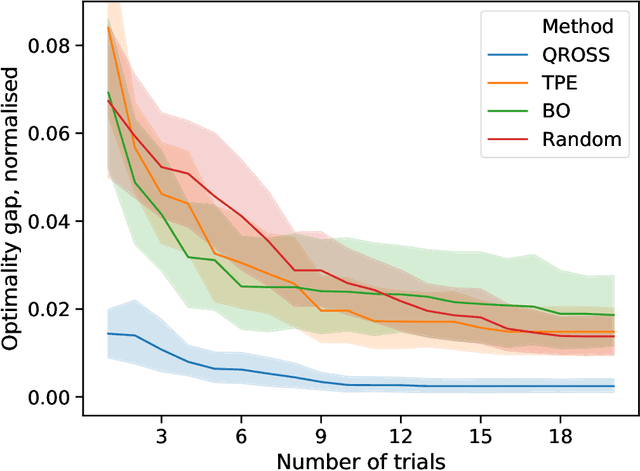
An increasingly popular method for solving a constrained combinatorial optimisation problem is to first convert it into a quadratic unconstrained binary optimisation (QUBO) problem, and solve it using a standard QUBO solver. However, this relaxation introduces hyper-parameters that balance the objective and penalty terms for the constraints, and their chosen values significantly impact performance. Hence, tuning these parameters is an important problem. Existing generic hyper-parameter tuning methods require multiple expensive calls to a QUBO solver, making them impractical for performance critical applications when repeated solutions of similar combinatorial optimisation problems are required. In this paper, we propose the QROSS method, in which we build surrogate models of QUBO solvers via learning from solver data on a collection of instances of a problem. In this way, we are able capture the common structure of the instances and their interactions with the solver, and produce good choices of penalty parameters with fewer number of calls to the QUBO solver. We take the Traveling Salesman Problem (TSP) as a case study, where we demonstrate that our method can find better solutions with fewer calls to QUBO solver compared with conventional hyper-parameter tuning techniques. Moreover, with simple adaptation methods, QROSS is shown to generalise well to out-of-distribution datasets and different types of QUBO solvers.

A Minimax Surrogate Loss Approach to Conditional Difference Estimation

We present a new machine learning approach to estimate personalized treatment effects in the classical potential outcomes framework with binary outcomes. To overcome the problem that both treatment and control outcomes for the same unit are required for supervised learning, we propose surrogate loss functions that incorporate both treatment and control data. The new surrogates yield tighter bounds than the sum of losses for treatment and control groups. A specific choice of loss function, namely a type of hinge loss, yields a minimax support vector machine formulation. The resulting optimization problem requires the solution to only a single convex optimization problem, incorporating both treatment and control units, and it enables the kernel trick to be used to handle nonlinear (also non-parametric) estimation. Statistical learning bounds are also presented for the framework, and experimental results.

Cascaded High Dimensional Histograms: A Generative Approach to Density Estimation

We present tree- and list- structured density estimation methods for high dimensional binary/categorical data. Our density estimation models are high dimensional analogies to variable bin width histograms. In each leaf of the tree (or list), the density is constant, similar to the flat density within the bin of a histogram. Histograms, however, cannot easily be visualized in higher dimensions, whereas our models can. The accuracy of histograms fades as dimensions increase, whereas our models have priors that help with generalization. Our models are sparse, unlike high-dimensional histograms. We present three generative models, where the first one allows the user to specify the number of desired leaves in the tree within a Bayesian prior. The second model allows the user to specify the desired number of branches within the prior. The third model returns lists (rather than trees) and allows the user to specify the desired number of rules and the length of rules within the prior. Our results indicate that the new approaches yield a better balance between sparsity and accuracy of density estimates than other methods for this task.

Box Drawings for Learning with Imbalanced Data

The vast majority of real world classification problems are imbalanced, meaning there are far fewer data from the class of interest (the positive class) than from other classes. We propose two machine learning algorithms to handle highly imbalanced classification problems. The classifiers constructed by both methods are created as unions of parallel axis rectangles around the positive examples, and thus have the benefit of being interpretable. The first algorithm uses mixed integer programming to optimize a weighted balance between positive and negative class accuracies. Regularization is introduced to improve generalization performance. The second method uses an approximation in order to assist with scalability. Specifically, it follows a \textit{characterize then discriminate} approach, where the positive class is characterized first by boxes, and then each box boundary becomes a separate discriminative classifier. This method has the computational advantages that it can be easily parallelized, and considers only the relevant regions of feature space.