QROSS: QUBO Relaxation Parameter Optimisation via Learning Solver Surrogates
Paper and Code
Mar 19, 2021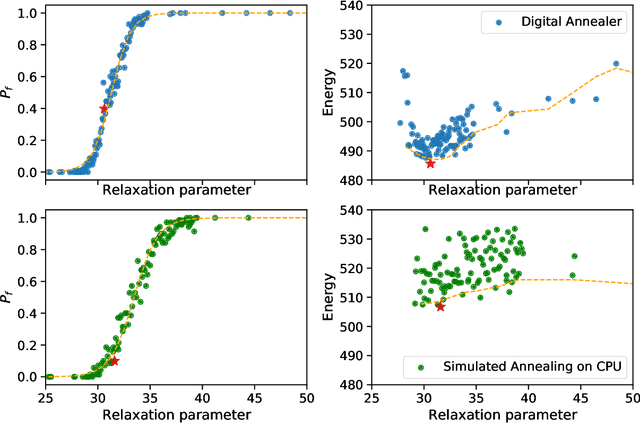
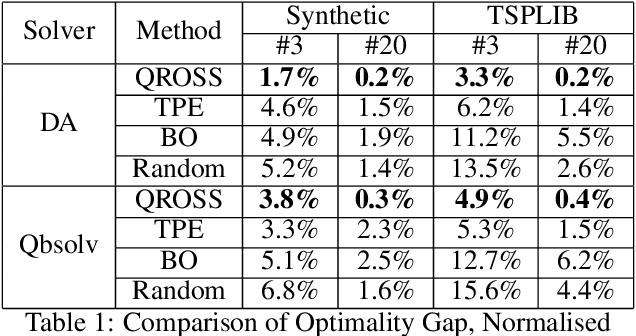
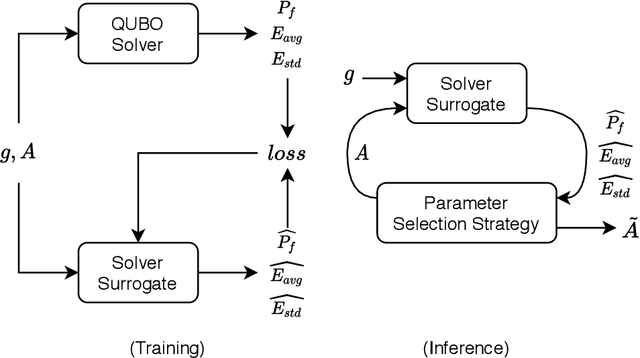
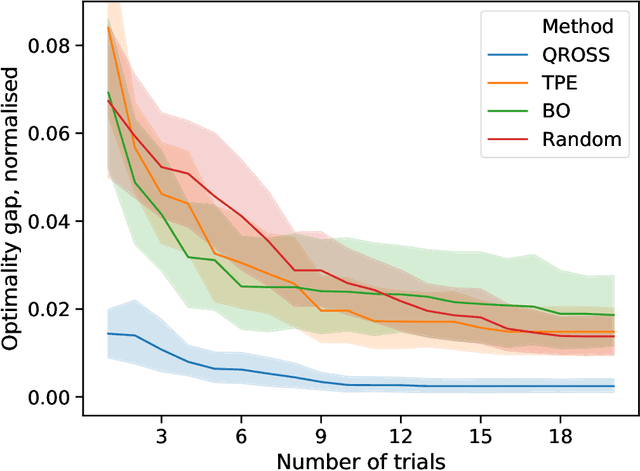
An increasingly popular method for solving a constrained combinatorial optimisation problem is to first convert it into a quadratic unconstrained binary optimisation (QUBO) problem, and solve it using a standard QUBO solver. However, this relaxation introduces hyper-parameters that balance the objective and penalty terms for the constraints, and their chosen values significantly impact performance. Hence, tuning these parameters is an important problem. Existing generic hyper-parameter tuning methods require multiple expensive calls to a QUBO solver, making them impractical for performance critical applications when repeated solutions of similar combinatorial optimisation problems are required. In this paper, we propose the QROSS method, in which we build surrogate models of QUBO solvers via learning from solver data on a collection of instances of a problem. In this way, we are able capture the common structure of the instances and their interactions with the solver, and produce good choices of penalty parameters with fewer number of calls to the QUBO solver. We take the Traveling Salesman Problem (TSP) as a case study, where we demonstrate that our method can find better solutions with fewer calls to QUBO solver compared with conventional hyper-parameter tuning techniques. Moreover, with simple adaptation methods, QROSS is shown to generalise well to out-of-distribution datasets and different types of QUBO solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge