Hermanni Heimonen
Noisy intermediate-scale quantum (NISQ) algorithms
Jan 21, 2021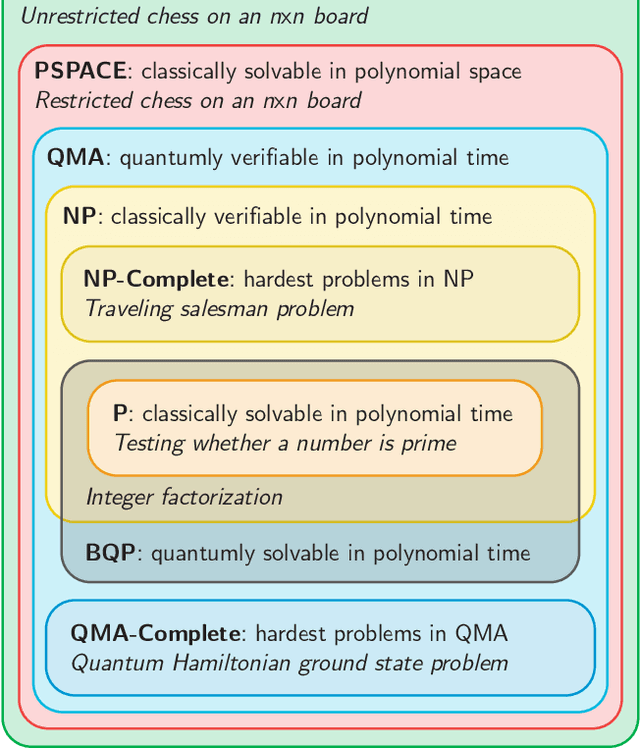
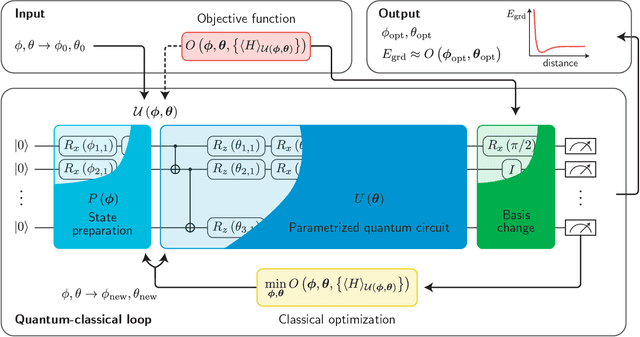
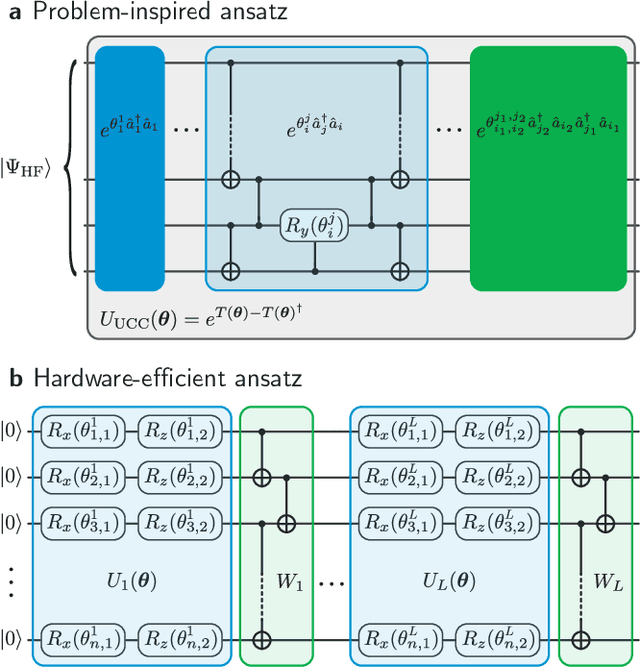
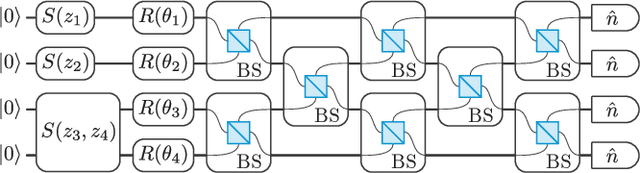
Abstract:A universal fault-tolerant quantum computer that can solve efficiently problems such as integer factorization and unstructured database search requires millions of qubits with low error rates and long coherence times. While the experimental advancement towards realizing such devices will potentially take decades of research, noisy intermediate-scale quantum (NISQ) computers already exist. These computers are composed of hundreds of noisy qubits, i.e. qubits that are not error-corrected, and therefore perform imperfect operations in a limited coherence time. In the search for quantum advantage with these devices, algorithms have been proposed for applications in various disciplines spanning physics, machine learning, quantum chemistry and combinatorial optimization. The goal of such algorithms is to leverage the limited available resources to perform classically challenging tasks. In this review, we provide a thorough summary of NISQ computational paradigms and algorithms. We discuss the key structure of these algorithms, their limitations, and advantages. We additionally provide a comprehensive overview of various benchmarking and software tools useful for programming and testing NISQ devices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge