Modelling the Distribution of Human Motion for Sign Language Assessment

Sign Language Assessment (SLA) tools are useful to aid in language learning and are underdeveloped. Previous work has focused on isolated signs or comparison against a single reference video to assess Sign Languages (SL). This paper introduces a novel SLA tool designed to evaluate the comprehensibility of SL by modelling the natural distribution of human motion. We train our pipeline on data from native signers and evaluate it using SL learners. We compare our results to ratings from a human raters study and find strong correlation between human ratings and our tool. We visually demonstrate our tools ability to detect anomalous results spatio-temporally, providing actionable feedback to aid in SL learning and assessment.

Generalization with quantum geometry for learning unitaries

Generalization is the ability of quantum machine learning models to make accurate predictions on new data by learning from training data. Here, we introduce the data quantum Fisher information metric (DQFIM) to determine when a model can generalize. For variational learning of unitaries, the DQFIM quantifies the amount of circuit parameters and training data needed to successfully train and generalize. We apply the DQFIM to explain when a constant number of training states and polynomial number of parameters are sufficient for generalization. Further, we can improve generalization by removing symmetries from training data. Finally, we show that out-of-distribution generalization, where training and testing data are drawn from different data distributions, can be better than using the same distribution. Our work opens up new approaches to improve generalization in quantum machine learning.

Large-scale quantum machine learning

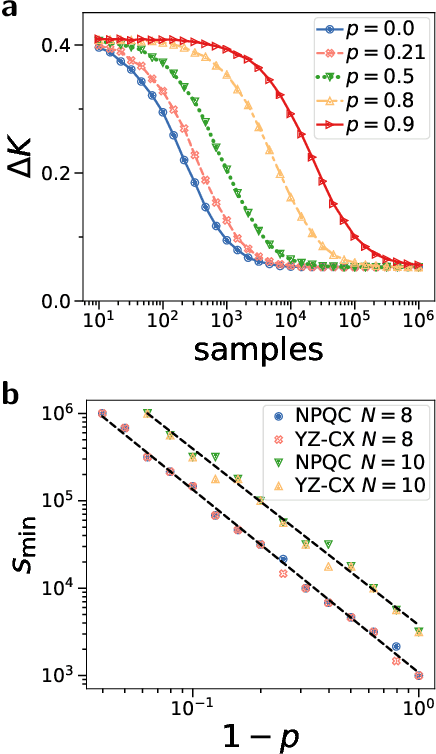
Quantum computers promise to enhance machine learning for practical applications. Quantum machine learning for real-world data has to handle extensive amounts of high-dimensional data. However, conventional methods for measuring quantum kernels are impractical for large datasets as they scale with the square of the dataset size. Here, we measure quantum kernels using randomized measurements to gain a quadratic speedup in computation time and quickly process large datasets. Further, we efficiently encode high-dimensional data into quantum computers with the number of features scaling linearly with the circuit depth. The encoding is characterized by the quantum Fisher information metric and is related to the radial basis function kernel. We demonstrate the advantages of our methods by classifying images with the IBM quantum computer. To achieve further speedups we distribute the quantum computational tasks between different quantum computers. Our approach is exceptionally robust to noise via a complementary error mitigation scheme. Using currently available quantum computers, the MNIST database can be processed within 220 hours instead of 10 years which opens up industrial applications of quantum machine learning.

NISQ Algorithm for Semidefinite Programming

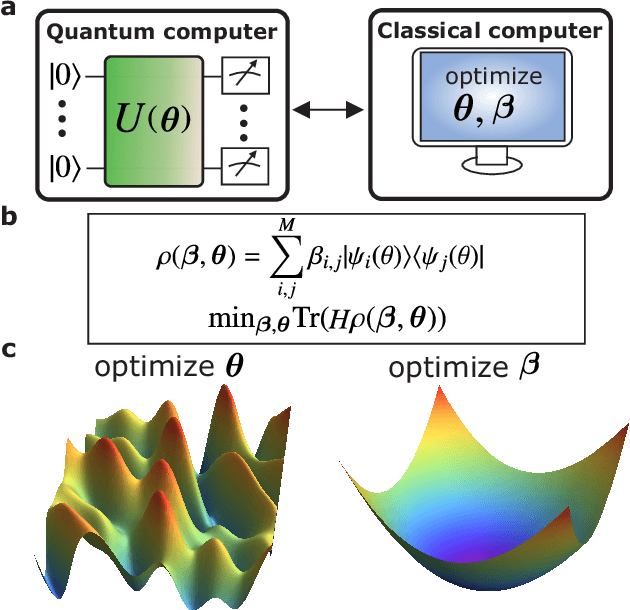
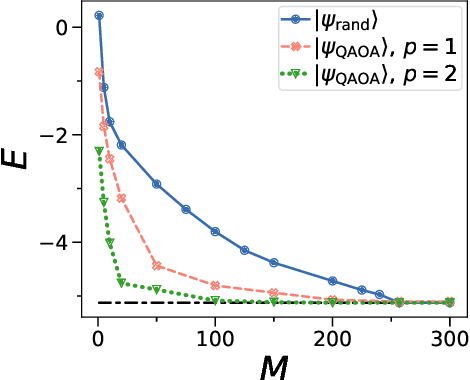
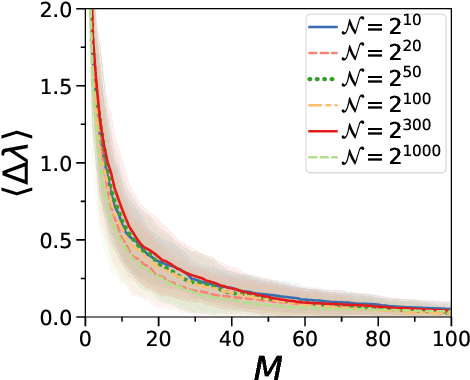
Semidefinite Programming (SDP) is a class of convex optimization programs with vast applications in control theory, quantum information, combinatorial optimization and operational research. Noisy intermediate-scale quantum (NISQ) algorithms aim to make an efficient use of the current generation of quantum hardware. However, optimizing variational quantum algorithms is a challenge as it is an NP-hard problem that in general requires an exponential time to solve and can contain many far from optimal local minima. Here, we present a current term NISQ algorithm for SDP. The classical optimization program of our NISQ solver is another SDP over a smaller dimensional ansatz space. We harness the SDP based formulation of the Hamiltonian ground state problem to design a NISQ eigensolver. Unlike variational quantum eigensolvers, the classical optimization program of our eigensolver is convex, can be solved in polynomial time with the number of ansatz parameters and every local minimum is a global minimum. Further, we demonstrate the potential of our NISQ SDP solver by finding the largest eigenvalue of up to $2^{1000}$ dimensional matrices and solving graph problems related to quantum contextuality. We also discuss NISQ algorithms for rank-constrained SDPs. Our work extends the application of NISQ computers onto one of the most successful algorithmic frameworks of the past few decades.

Optimal training of variational quantum algorithms without barren plateaus

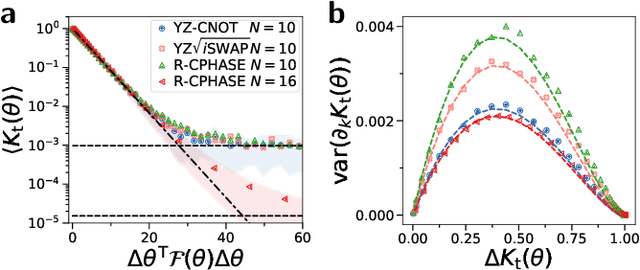
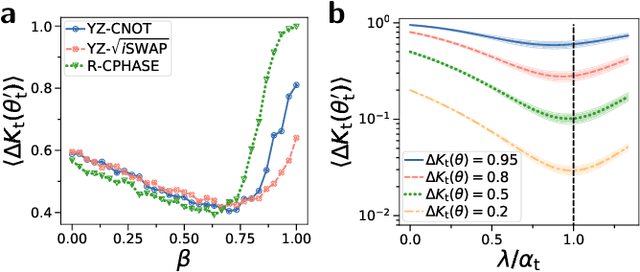
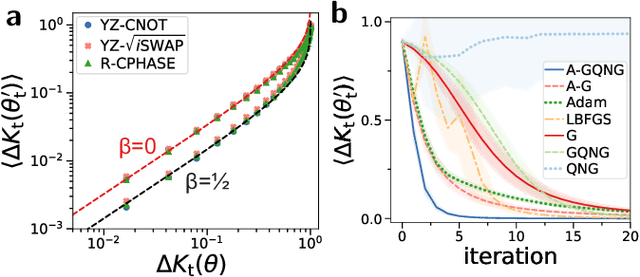
Variational quantum algorithms (VQAs) promise efficient use of near-term quantum computers. However, training VQAs often requires an extensive amount of time and suffers from the barren plateau problem where the magnitude of the gradients vanishes with increasing number of qubits. Here, we show how to optimally train a VQA for learning quantum states. Parameterized quantum circuits can form Gaussian kernels, which we use to derive optimal adaptive learning rates for gradient ascent. We introduce the generalized quantum natural gradient that features stability and optimized movement in parameter space. Both methods together outperform other optimization routines and can enhance VQAs as well as quantum control techniques. The gradients of the VQA do not vanish when the fidelity between the initial state and the state to be learned is bounded from below. We identify a VQA for quantum simulation with such a constraint that thus can be trained free of barren plateaus. Finally, we propose the application of Gaussian kernels for quantum machine learning.

Capacity and quantum geometry of parametrized quantum circuits

To harness the potential of noisy intermediate-scale quantum devices, it is paramount to find the best type of circuits to run hybrid quantum-classical algorithms. Key candidates are parametrized quantum circuits that can be effectively implemented on current devices. Here, we evaluate the capacity and trainability of these circuits using the geometric structure of the parameter space via the effective quantum dimension, which reveals the expressive power of circuits in general as well as of particular initialization strategies. We assess the representation power of various popular circuit types and find striking differences depending on the type of entangling gates used. Particular circuits are characterized by scaling laws in their expressiveness. We identify a transition in the quantum geometry of the parameter space, which leads to a decay of the quantum natural gradient for deep circuits. For shallow circuits, the quantum natural gradient can be orders of magnitude larger in value compared to the regular gradient; however, both of them can suffer from vanishing gradients. By tuning a fixed set of circuit parameters to randomized ones, we find a region where the circuit is expressive, but does not suffer from barren plateaus, hinting at a good way to initialize circuits. Our results enhance the understanding of parametrized quantum circuits for improving variational quantum algorithms.

Noisy intermediate-scale quantum (NISQ) algorithms

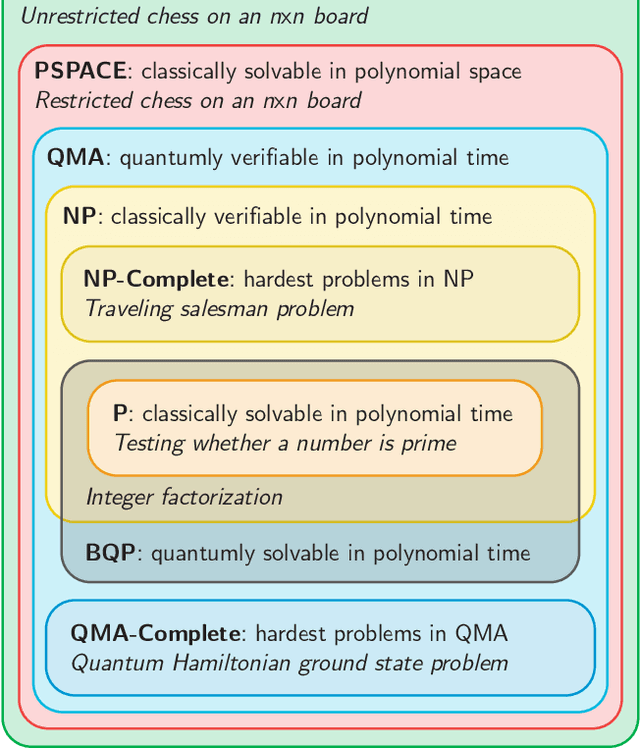
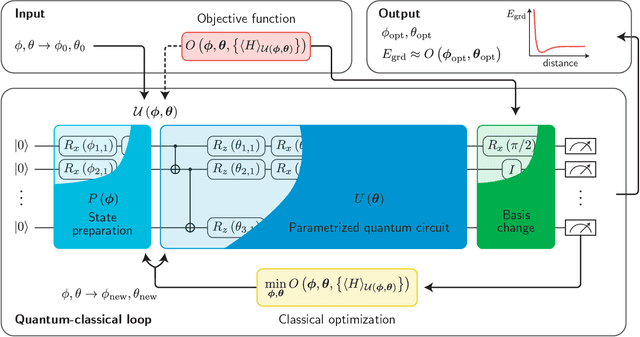
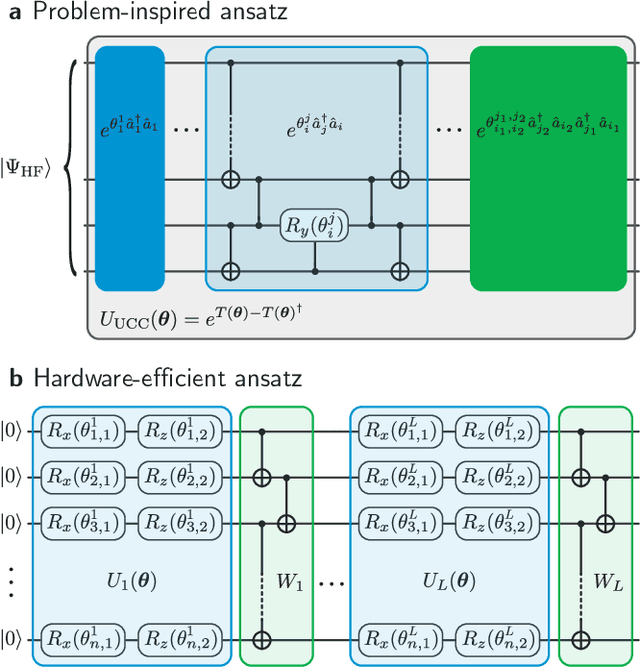
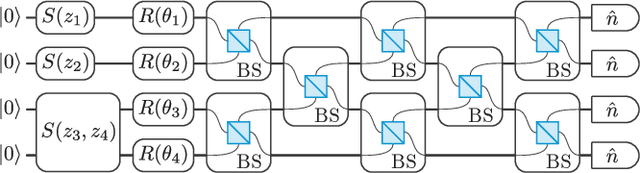
A universal fault-tolerant quantum computer that can solve efficiently problems such as integer factorization and unstructured database search requires millions of qubits with low error rates and long coherence times. While the experimental advancement towards realizing such devices will potentially take decades of research, noisy intermediate-scale quantum (NISQ) computers already exist. These computers are composed of hundreds of noisy qubits, i.e. qubits that are not error-corrected, and therefore perform imperfect operations in a limited coherence time. In the search for quantum advantage with these devices, algorithms have been proposed for applications in various disciplines spanning physics, machine learning, quantum chemistry and combinatorial optimization. The goal of such algorithms is to leverage the limited available resources to perform classically challenging tasks. In this review, we provide a thorough summary of NISQ computational paradigms and algorithms. We discuss the key structure of these algorithms, their limitations, and advantages. We additionally provide a comprehensive overview of various benchmarking and software tools useful for programming and testing NISQ devices.