Optimal training of variational quantum algorithms without barren plateaus

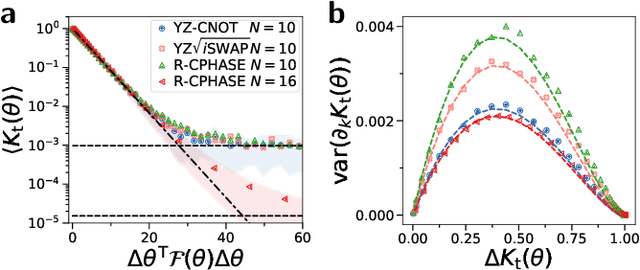
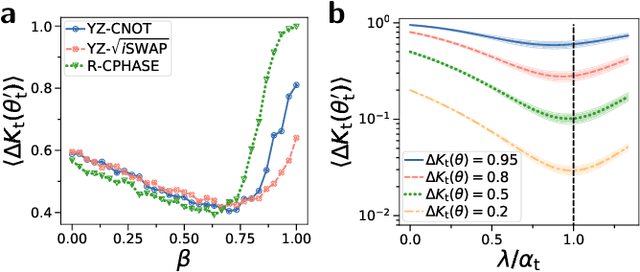
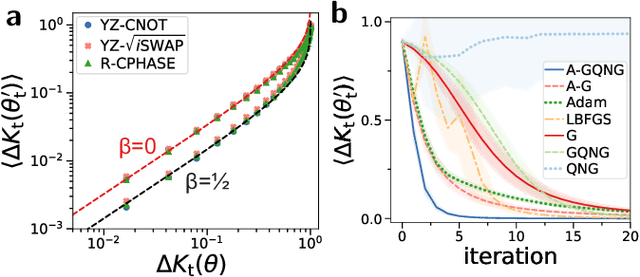
Variational quantum algorithms (VQAs) promise efficient use of near-term quantum computers. However, training VQAs often requires an extensive amount of time and suffers from the barren plateau problem where the magnitude of the gradients vanishes with increasing number of qubits. Here, we show how to optimally train a VQA for learning quantum states. Parameterized quantum circuits can form Gaussian kernels, which we use to derive optimal adaptive learning rates for gradient ascent. We introduce the generalized quantum natural gradient that features stability and optimized movement in parameter space. Both methods together outperform other optimization routines and can enhance VQAs as well as quantum control techniques. The gradients of the VQA do not vanish when the fidelity between the initial state and the state to be learned is bounded from below. We identify a VQA for quantum simulation with such a constraint that thus can be trained free of barren plateaus. Finally, we propose the application of Gaussian kernels for quantum machine learning.