Assessing Quantum Advantage for Gaussian Process Regression

Gaussian Process Regression is a well-known machine learning technique for which several quantum algorithms have been proposed. We show here that in a wide range of scenarios these algorithms show no exponential speedup. We achieve this by rigorously proving that the condition number of a kernel matrix scales at least linearly with the matrix size under general assumptions on the data and kernel. We additionally prove that the sparsity and Frobenius norm of a kernel matrix scale linearly under similar assumptions. The implications for the quantum algorithms runtime are independent of the complexity of loading classical data on a quantum computer and also apply to dequantised algorithms. We supplement our theoretical analysis with numerical verification for popular kernels in machine learning.

Generalization with quantum geometry for learning unitaries

Generalization is the ability of quantum machine learning models to make accurate predictions on new data by learning from training data. Here, we introduce the data quantum Fisher information metric (DQFIM) to determine when a model can generalize. For variational learning of unitaries, the DQFIM quantifies the amount of circuit parameters and training data needed to successfully train and generalize. We apply the DQFIM to explain when a constant number of training states and polynomial number of parameters are sufficient for generalization. Further, we can improve generalization by removing symmetries from training data. Finally, we show that out-of-distribution generalization, where training and testing data are drawn from different data distributions, can be better than using the same distribution. Our work opens up new approaches to improve generalization in quantum machine learning.

Faster variational quantum algorithms with quantum kernel-based surrogate models

We present a new optimization method for small-to-intermediate scale variational algorithms on noisy near-term quantum processors which uses a Gaussian process surrogate model equipped with a classically-evaluated quantum kernel. Variational algorithms are typically optimized using gradient-based approaches however these are difficult to implement on current noisy devices, requiring large numbers of objective function evaluations. Our scheme shifts this computational burden onto the classical optimizer component of these hybrid algorithms, greatly reducing the number of queries to the quantum processor. We focus on the variational quantum eigensolver (VQE) algorithm and demonstrate numerically that such surrogate models are particularly well suited to the algorithm's objective function. Next, we apply these models to both noiseless and noisy VQE simulations and show that they exhibit better performance than widely-used classical kernels in terms of final accuracy and convergence speed. Compared to the typically-used stochastic gradient-descent approach for VQAs, our quantum kernel-based approach is found to consistently achieve significantly higher accuracy while requiring less than an order of magnitude fewer quantum circuit evaluations. We analyse the performance of the quantum kernel-based models in terms of the kernels' induced feature spaces and explicitly construct their feature maps. Finally, we describe a scheme for approximating the best-performing quantum kernel using a classically-efficient tensor network representation of its input state and so provide a pathway for scaling these methods to larger systems.

Large-scale quantum machine learning

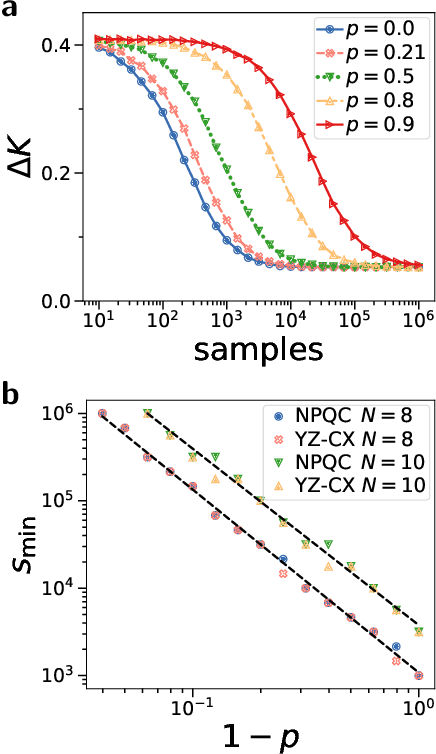
Quantum computers promise to enhance machine learning for practical applications. Quantum machine learning for real-world data has to handle extensive amounts of high-dimensional data. However, conventional methods for measuring quantum kernels are impractical for large datasets as they scale with the square of the dataset size. Here, we measure quantum kernels using randomized measurements to gain a quadratic speedup in computation time and quickly process large datasets. Further, we efficiently encode high-dimensional data into quantum computers with the number of features scaling linearly with the circuit depth. The encoding is characterized by the quantum Fisher information metric and is related to the radial basis function kernel. We demonstrate the advantages of our methods by classifying images with the IBM quantum computer. To achieve further speedups we distribute the quantum computational tasks between different quantum computers. Our approach is exceptionally robust to noise via a complementary error mitigation scheme. Using currently available quantum computers, the MNIST database can be processed within 220 hours instead of 10 years which opens up industrial applications of quantum machine learning.

Optimal training of variational quantum algorithms without barren plateaus

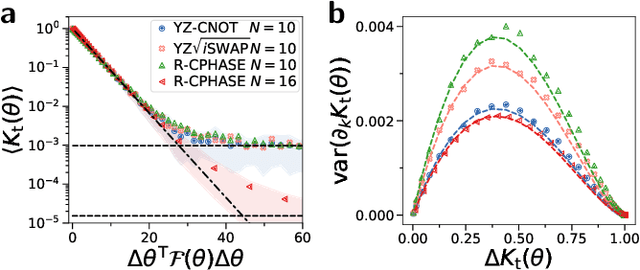
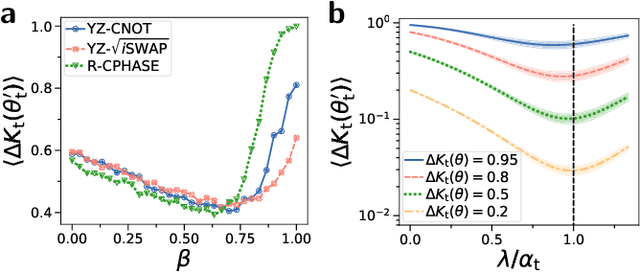
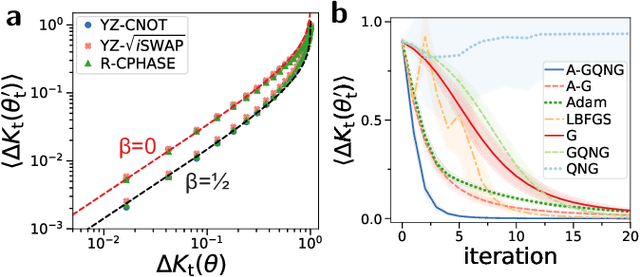
Variational quantum algorithms (VQAs) promise efficient use of near-term quantum computers. However, training VQAs often requires an extensive amount of time and suffers from the barren plateau problem where the magnitude of the gradients vanishes with increasing number of qubits. Here, we show how to optimally train a VQA for learning quantum states. Parameterized quantum circuits can form Gaussian kernels, which we use to derive optimal adaptive learning rates for gradient ascent. We introduce the generalized quantum natural gradient that features stability and optimized movement in parameter space. Both methods together outperform other optimization routines and can enhance VQAs as well as quantum control techniques. The gradients of the VQA do not vanish when the fidelity between the initial state and the state to be learned is bounded from below. We identify a VQA for quantum simulation with such a constraint that thus can be trained free of barren plateaus. Finally, we propose the application of Gaussian kernels for quantum machine learning.

Capacity and quantum geometry of parametrized quantum circuits

To harness the potential of noisy intermediate-scale quantum devices, it is paramount to find the best type of circuits to run hybrid quantum-classical algorithms. Key candidates are parametrized quantum circuits that can be effectively implemented on current devices. Here, we evaluate the capacity and trainability of these circuits using the geometric structure of the parameter space via the effective quantum dimension, which reveals the expressive power of circuits in general as well as of particular initialization strategies. We assess the representation power of various popular circuit types and find striking differences depending on the type of entangling gates used. Particular circuits are characterized by scaling laws in their expressiveness. We identify a transition in the quantum geometry of the parameter space, which leads to a decay of the quantum natural gradient for deep circuits. For shallow circuits, the quantum natural gradient can be orders of magnitude larger in value compared to the regular gradient; however, both of them can suffer from vanishing gradients. By tuning a fixed set of circuit parameters to randomized ones, we find a region where the circuit is expressive, but does not suffer from barren plateaus, hinting at a good way to initialize circuits. Our results enhance the understanding of parametrized quantum circuits for improving variational quantum algorithms.

Efficient Approximate Quantum State Tomography with Basis Dependent Neural-Networks

We use a meta-learning neural-network approach to predict measurement outcomes of a quantum state in arbitrary local bases and thus carry out an approximate quantum state tomography. Each stage of this procedure can be performed efficiently, allowing it to be used effectively on large systems. We demonstrate this approach on the most recent noisy intermediate-scale IBM Quantum devices, achieving an accurate generative model for a 6-qubit state's measurement outcomes with only 100 random measurement settings as opposed to the 729 settings required for full tomography. This reduction in the required number of measurements scales favourably, with around 200 measurement settings yielding good results for a 10 qubit state that would require 59,049 settings for full quantum state tomography. This reduction in the number of measurement settings coupled with the efficiency of the procedure could allow for estimations of expectation values and state fidelities in practicable times on current quantum devices. For suitable states, this could then help in increasing the speed of other optimization schemes when attempting to produce states on noisy quantum devices at a scale where traditional maximum likelihood based approaches are impractical.