A photonic chip-based machine learning approach for the prediction of molecular properties

Machine learning methods have revolutionized the discovery process of new molecules and materials. However, the intensive training process of neural networks for molecules with ever increasing complexity has resulted in exponential growth in computation cost, leading to long simulation time and high energy consumption. Photonic chip technology offers an alternative platform for implementing neural network with faster data processing and lower energy usage compared to digital computers. Here, we demonstrate the capability of photonic neural networks in predicting the quantum mechanical properties of molecules. Additionally, we show that multiple properties can be learned simultaneously in a photonic chip via a multi-task regression learning algorithm, which we believe is the first of its kind, as most previous works focus on implementing a network for the task of classification. Photonics technology are also naturally capable of implementing complex-valued neural networks at no additional hardware cost and we show that such neural networks outperform conventional real-valued networks for molecular property prediction. Our work opens the avenue for harnessing photonic technology for large-scale machine learning applications in molecular sciences such as drug discovery and materials design.

NISQ Algorithm for Semidefinite Programming

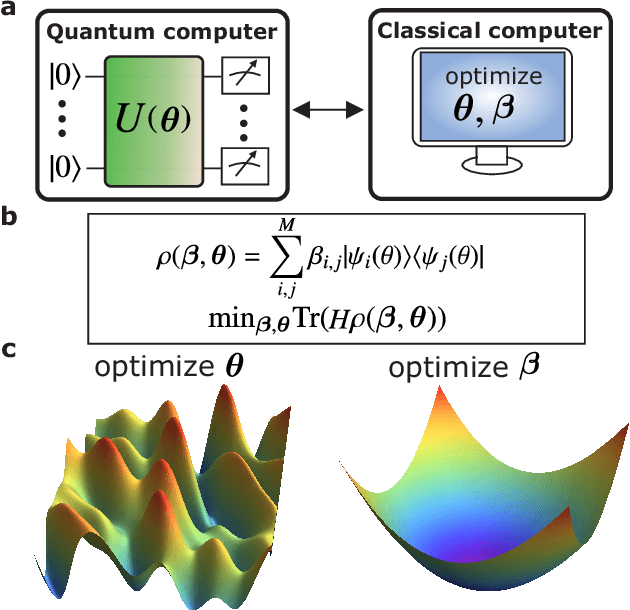
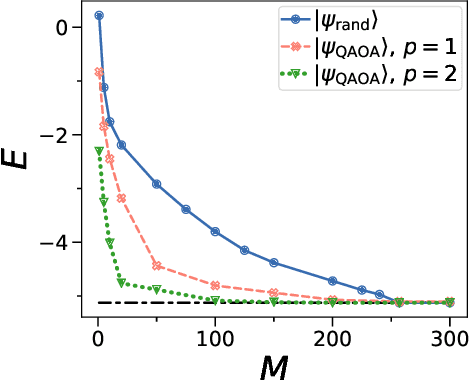
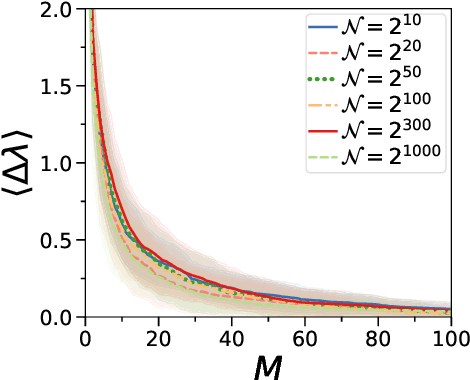
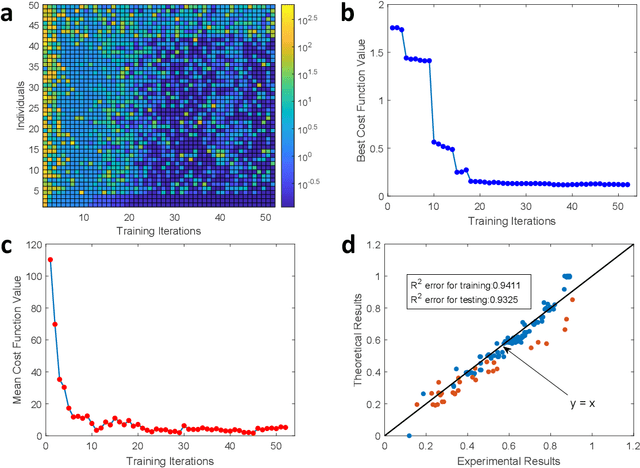
Semidefinite Programming (SDP) is a class of convex optimization programs with vast applications in control theory, quantum information, combinatorial optimization and operational research. Noisy intermediate-scale quantum (NISQ) algorithms aim to make an efficient use of the current generation of quantum hardware. However, optimizing variational quantum algorithms is a challenge as it is an NP-hard problem that in general requires an exponential time to solve and can contain many far from optimal local minima. Here, we present a current term NISQ algorithm for SDP. The classical optimization program of our NISQ solver is another SDP over a smaller dimensional ansatz space. We harness the SDP based formulation of the Hamiltonian ground state problem to design a NISQ eigensolver. Unlike variational quantum eigensolvers, the classical optimization program of our eigensolver is convex, can be solved in polynomial time with the number of ansatz parameters and every local minimum is a global minimum. Further, we demonstrate the potential of our NISQ SDP solver by finding the largest eigenvalue of up to $2^{1000}$ dimensional matrices and solving graph problems related to quantum contextuality. We also discuss NISQ algorithms for rank-constrained SDPs. Our work extends the application of NISQ computers onto one of the most successful algorithmic frameworks of the past few decades.

Noisy intermediate-scale quantum (NISQ) algorithms

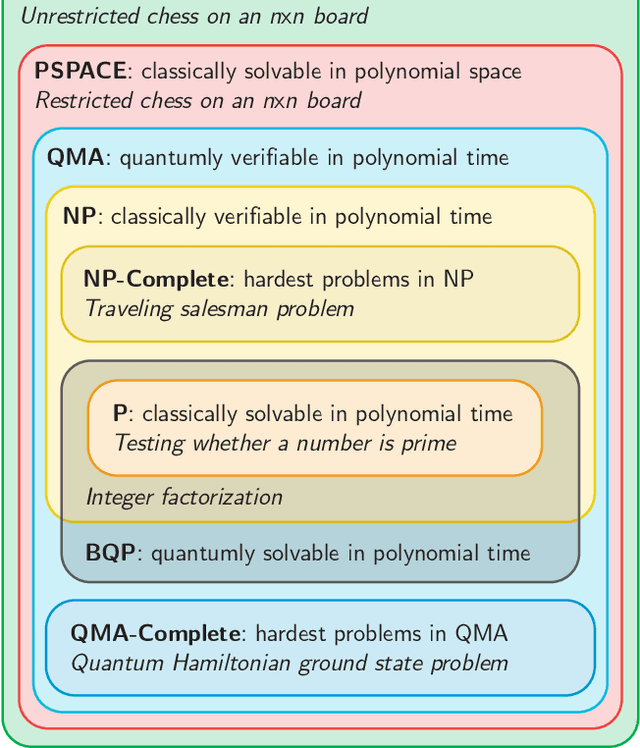
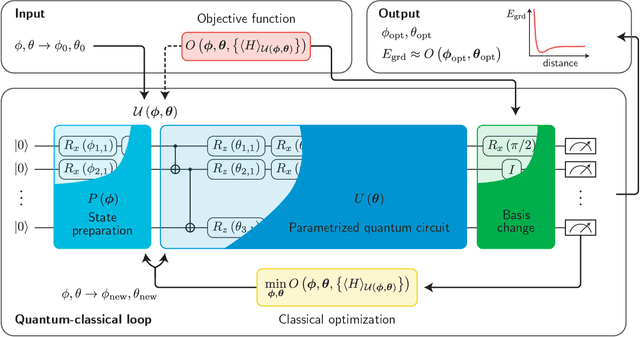
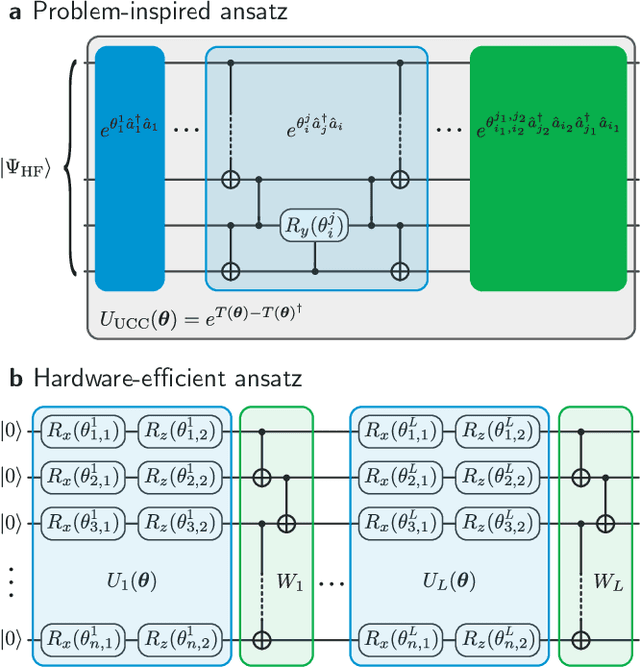
A universal fault-tolerant quantum computer that can solve efficiently problems such as integer factorization and unstructured database search requires millions of qubits with low error rates and long coherence times. While the experimental advancement towards realizing such devices will potentially take decades of research, noisy intermediate-scale quantum (NISQ) computers already exist. These computers are composed of hundreds of noisy qubits, i.e. qubits that are not error-corrected, and therefore perform imperfect operations in a limited coherence time. In the search for quantum advantage with these devices, algorithms have been proposed for applications in various disciplines spanning physics, machine learning, quantum chemistry and combinatorial optimization. The goal of such algorithms is to leverage the limited available resources to perform classically challenging tasks. In this review, we provide a thorough summary of NISQ computational paradigms and algorithms. We discuss the key structure of these algorithms, their limitations, and advantages. We additionally provide a comprehensive overview of various benchmarking and software tools useful for programming and testing NISQ devices.