NISQ Algorithm for Semidefinite Programming
Paper and Code
Jun 07, 2021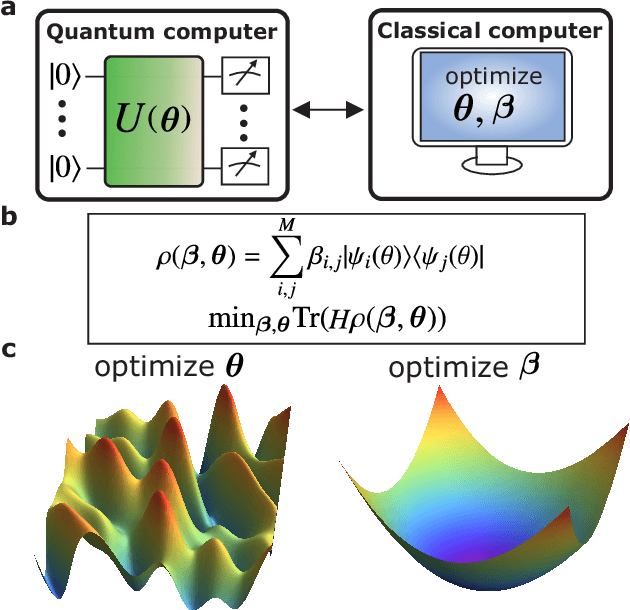
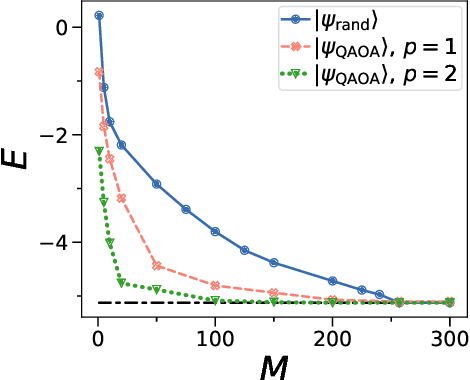
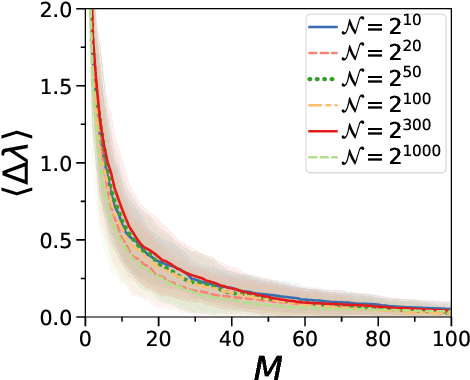
Semidefinite Programming (SDP) is a class of convex optimization programs with vast applications in control theory, quantum information, combinatorial optimization and operational research. Noisy intermediate-scale quantum (NISQ) algorithms aim to make an efficient use of the current generation of quantum hardware. However, optimizing variational quantum algorithms is a challenge as it is an NP-hard problem that in general requires an exponential time to solve and can contain many far from optimal local minima. Here, we present a current term NISQ algorithm for SDP. The classical optimization program of our NISQ solver is another SDP over a smaller dimensional ansatz space. We harness the SDP based formulation of the Hamiltonian ground state problem to design a NISQ eigensolver. Unlike variational quantum eigensolvers, the classical optimization program of our eigensolver is convex, can be solved in polynomial time with the number of ansatz parameters and every local minimum is a global minimum. Further, we demonstrate the potential of our NISQ SDP solver by finding the largest eigenvalue of up to $2^{1000}$ dimensional matrices and solving graph problems related to quantum contextuality. We also discuss NISQ algorithms for rank-constrained SDPs. Our work extends the application of NISQ computers onto one of the most successful algorithmic frameworks of the past few decades.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge