Protecting Confidentiality, Privacy and Integrity in Collaborative Learning

A collaboration between dataset owners and model owners is needed to facilitate effective machine learning (ML) training. During this collaboration, however, dataset owners and model owners want to protect the confidentiality of their respective assets (i.e., datasets, models and training code), with the dataset owners also caring about the privacy of individual users whose data is in their datasets. Existing solutions either provide limited confidentiality for models and training code, or suffer from privacy issues due to collusion. We present Citadel++, a scalable collaborative ML training system designed to simultaneously protect the confidentiality of datasets, models and training code, as well as the privacy of individual users. Citadel++ enhances differential privacy techniques to safeguard the privacy of individual user data while maintaining model utility. By employing Virtual Machine-level Trusted Execution Environments (TEEs) and improved integrity protection techniques through various OS-level mechanisms, Citadel++ effectively preserves the confidentiality of datasets, models and training code, and enforces our privacy mechanisms even when the models and training code have been maliciously designed. Our experiments show that Citadel++ provides privacy, model utility and performance while adhering to confidentiality and privacy requirements of dataset owners and model owners, outperforming the state-of-the-art privacy-preserving training systems by up to 543x on CPU and 113x on GPU TEEs.

Differentially Private Convex Approximation of Two-Layer ReLU Networks

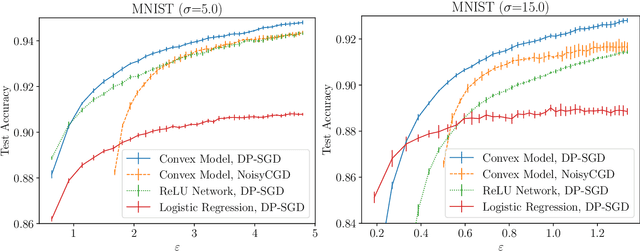
We show that it is possible to privately train convex problems that give models with similar privacy-utility trade-off as one hidden-layer ReLU networks trained with differentially private stochastic gradient descent (DP-SGD). As we show, this is possible via a certain dual formulation of the ReLU minimization problem. We derive a stochastic approximation of the dual problem that leads to a strongly convex problem which allows applying, for example, the privacy amplification by iteration type of analysis for gradient-based private optimizers, and in particular allows giving accurate privacy bounds for the noisy cyclic mini-batch gradient descent with fixed disjoint mini-batches. We obtain on the MNIST and FashionMNIST problems for the noisy cyclic mini-batch gradient descent first empirical results that show similar privacy-utility-trade-offs as DP-SGD applied to a ReLU network. We outline theoretical utility bounds that illustrate the speed-ups of the private convex approximation of ReLU networks.

Black Box Differential Privacy Auditing Using Total Variation Distance

We present a practical method to audit the differential privacy (DP) guarantees of a machine learning model using a small hold-out dataset that is not exposed to the model during the training. Having a score function such as the loss function employed during the training, our method estimates the total variation (TV) distance between scores obtained with a subset of the training data and the hold-out dataset. With some meta information about the underlying DP training algorithm, these TV distance values can be converted to $(\varepsilon,\delta)$-guarantees for any $\delta$. We show that these score distributions asymptotically give lower bounds for the DP guarantees of the underlying training algorithm, however, we perform a one-shot estimation for practicality reasons. We specify conditions that lead to lower bounds for the DP guarantees with high probability. To estimate the TV distance between the score distributions, we use a simple density estimation method based on histograms. We show that the TV distance gives a very close to optimally robust estimator and has an error rate $\mathcal{O}(k^{-1/3})$, where $k$ is the total number of samples. Numerical experiments on benchmark datasets illustrate the effectiveness of our approach and show improvements over baseline methods for black-box auditing.

Privacy Profiles for Private Selection

Private selection mechanisms (e.g., Report Noisy Max, Sparse Vector) are fundamental primitives of differentially private (DP) data analysis with wide applications to private query release, voting, and hyperparameter tuning. Recent work (Liu and Talwar, 2019; Papernot and Steinke, 2022) has made significant progress in both generalizing private selection mechanisms and tightening their privacy analysis using modern numerical privacy accounting tools, e.g., R\'enyi DP. But R\'enyi DP is known to be lossy when $(\epsilon,\delta)$-DP is ultimately needed, and there is a trend to close the gap by directly handling privacy profiles, i.e., $\delta$ as a function of $\epsilon$ or its equivalent dual form known as $f$-DPs. In this paper, we work out an easy-to-use recipe that bounds the privacy profiles of ReportNoisyMax and PrivateTuning using the privacy profiles of the base algorithms they corral. Numerically, our approach improves over the RDP-based accounting in all regimes of interest and leads to substantial benefits in end-to-end private learning experiments. Our analysis also suggests new distributions, e.g., binomial distribution for randomizing the number of rounds that leads to more substantial improvements in certain regimes.

Improving the Privacy and Practicality of Objective Perturbation for Differentially Private Linear Learners

In the arena of privacy-preserving machine learning, differentially private stochastic gradient descent (DP-SGD) has outstripped the objective perturbation mechanism in popularity and interest. Though unrivaled in versatility, DP-SGD requires a non-trivial privacy overhead (for privately tuning the model's hyperparameters) and a computational complexity which might be extravagant for simple models such as linear and logistic regression. This paper revamps the objective perturbation mechanism with tighter privacy analyses and new computational tools that boost it to perform competitively with DP-SGD on unconstrained convex generalized linear problems.

Practical Differentially Private Hyperparameter Tuning with Subsampling

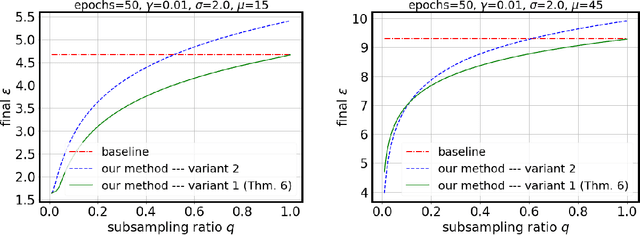
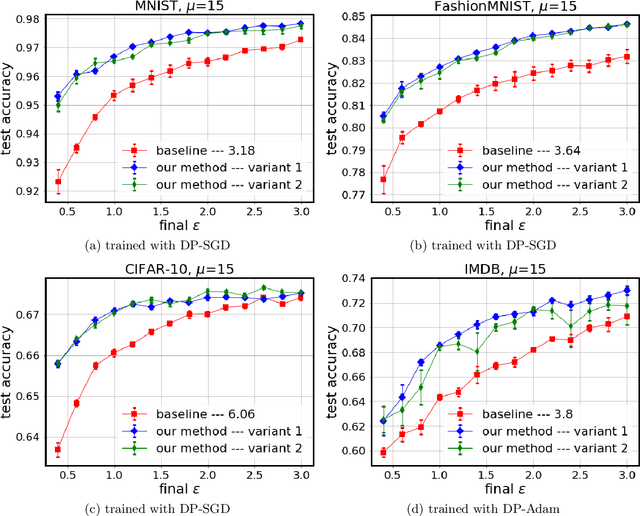
Tuning all the hyperparameters of differentially private (DP) machine learning (ML) algorithms often requires use of sensitive data and this may leak private information via hyperparameter values. Recently, Papernot and Steinke (2022) proposed a certain class of DP hyperparameter tuning algorithms, where the number of random search samples is randomized itself. Commonly, these algorithms still considerably increase the DP privacy parameter $\varepsilon$ over non-tuned DP ML model training and can be computationally heavy as evaluating each hyperparameter candidate requires a new training run. We focus on lowering both the DP bounds and the computational complexity of these methods by using only a random subset of the sensitive data for the hyperparameter tuning and by extrapolating the optimal values from the small dataset to a larger dataset. We provide a R\'enyi differential privacy analysis for the proposed method and experimentally show that it consistently leads to better privacy-utility trade-off than the baseline method by Papernot and Steinke (2022).

Individual Privacy Accounting with Gaussian Differential Privacy

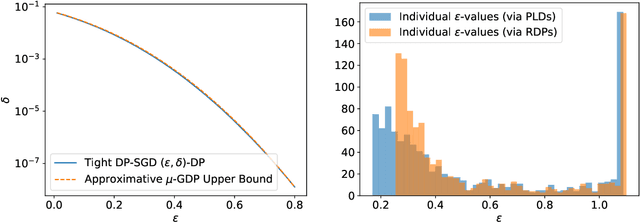
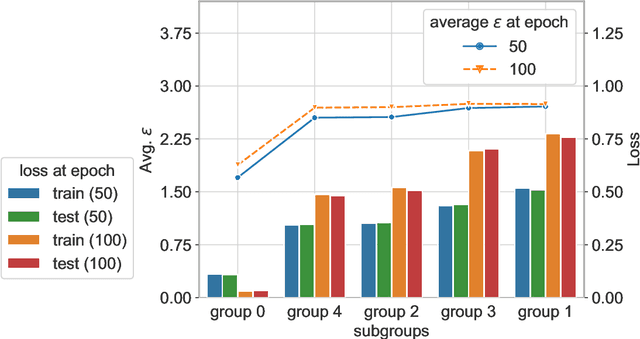
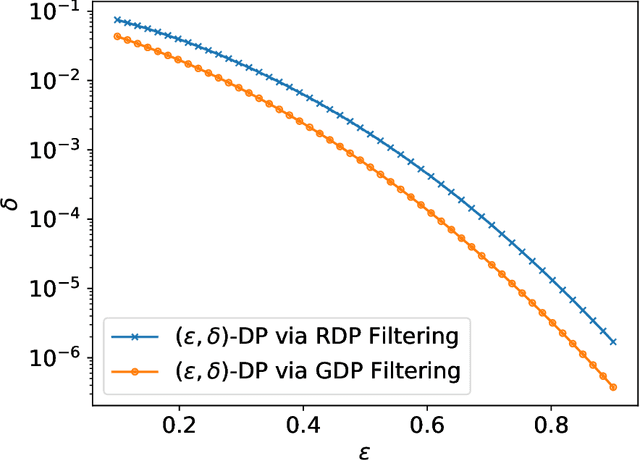
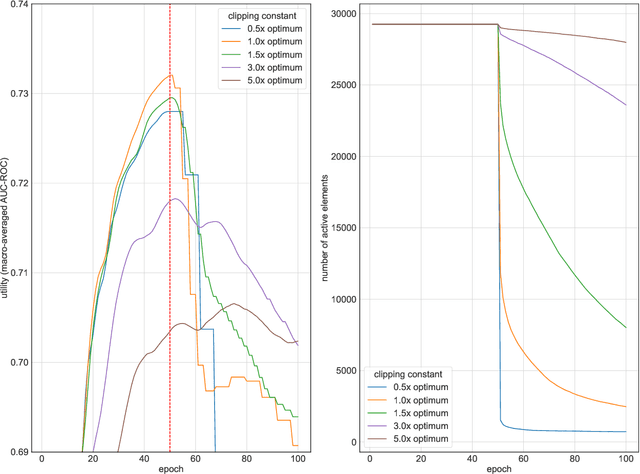
Individual privacy accounting enables bounding differential privacy (DP) loss individually for each participant involved in the analysis. This can be informative as often the individual privacy losses are considerably smaller than those indicated by the DP bounds that are based on considering worst-case bounds at each data access. In order to account for the individual privacy losses in a principled manner, we need a privacy accountant for adaptive compositions of randomised mechanisms, where the loss incurred at a given data access is allowed to be smaller than the worst-case loss. This kind of analysis has been carried out for the R\'enyi differential privacy (RDP) by Feldman and Zrnic (2021), however not yet for the so-called optimal privacy accountants. We make first steps in this direction by providing a careful analysis using the Gaussian differential privacy which gives optimal bounds for the Gaussian mechanism, one of the most versatile DP mechanisms. This approach is based on determining a certain supermartingale for the hockey-stick divergence and on extending the R\'enyi divergence-based fully adaptive composition results by Feldman and Zrnic (2021). We also consider measuring the individual $(\varepsilon,\delta)$-privacy losses using the so-called privacy loss distributions. With the help of the Blackwell theorem, we can then make use of the RDP analysis to construct an approximative individual $(\varepsilon,\delta)$-accountant.

Tight Accounting in the Shuffle Model of Differential Privacy

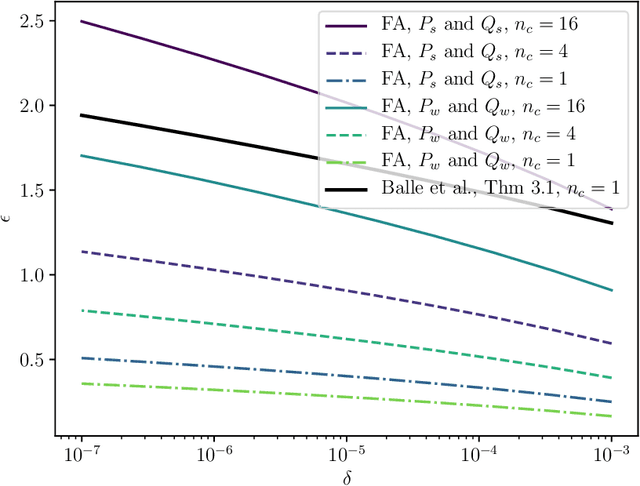
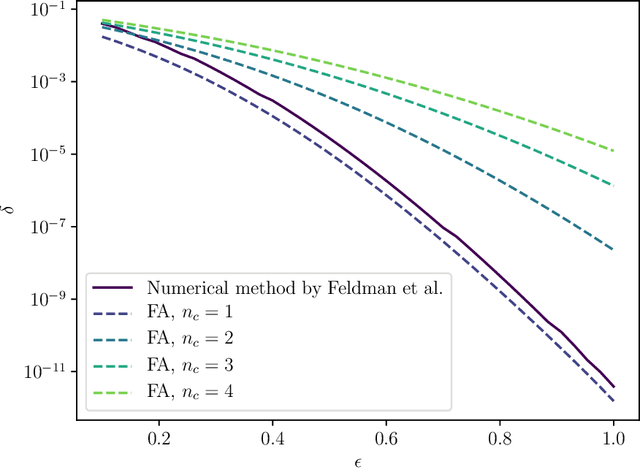
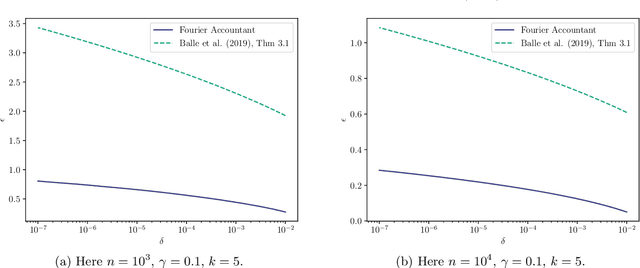
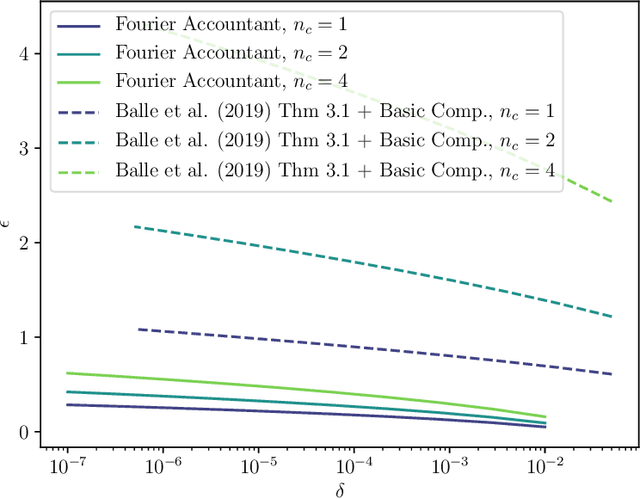
Shuffle model of differential privacy is a novel distributed privacy model based on a combination of local privacy mechanisms and a trusted shuffler. It has been shown that the additional randomisation provided by the shuffler improves privacy bounds compared to the purely local mechanisms. Accounting tight bounds, especially for multi-message protocols, is complicated by the complexity brought by the shuffler. The recently proposed Fourier Accountant for evaluating $(\varepsilon,\delta)$-differential privacy guarantees has been shown to give tighter bounds than commonly used methods for non-adaptive compositions of various complex mechanisms. In this paper we show how to compute tight privacy bounds using the Fourier Accountant for multi-message versions of several ubiquitous mechanisms in the shuffle model and demonstrate looseness of the existing bounds in the literature.

Computing Differential Privacy Guarantees for Heterogeneous Compositions Using FFT

The recently proposed Fast Fourier Transform (FFT)-based accountant for evaluating $(\varepsilon,\delta)$-differential privacy guarantees using the privacy loss distribution formalism has been shown to give tighter bounds than commonly used methods such as R\'enyi accountants when applied to compositions of homogeneous mechanisms. This approach is also applicable to certain discrete mechanisms that cannot be analysed with R\'enyi accountants. In this paper, we extend this approach to compositions of heterogeneous mechanisms. We carry out a full error analysis that allows choosing the parameters of the algorithm such that a desired accuracy is obtained. Using our analysis, we also give a bound for the computational complexity in terms of the error which is analogous to and slightly tightens the one given by Murtagh and Vadhan (2018). We also show how to speed up the evaluation of tight privacy guarantees using the Plancherel theorem at the cost of increased pre-computation and memory usage.

Differentially Private Bayesian Inference for Generalized Linear Models

The framework of differential privacy (DP) upper bounds the information disclosure risk involved in using sensitive datasets for statistical analysis. A DP mechanism typically operates by adding carefully calibrated noise to the data release procedure. Generalized linear models (GLMs) are among the most widely used arms in data analyst's repertoire. In this work, with logistic and Poisson regression as running examples, we propose a generic noise-aware Bayesian framework to quantify the parameter uncertainty for a GLM at hand, given noisy sufficient statistics. We perform a tight privacy analysis and experimentally demonstrate that the posteriors obtained from our model, while adhering to strong privacy guarantees, are similar to the non-private posteriors.