Computing Differential Privacy Guarantees for Heterogeneous Compositions Using FFT

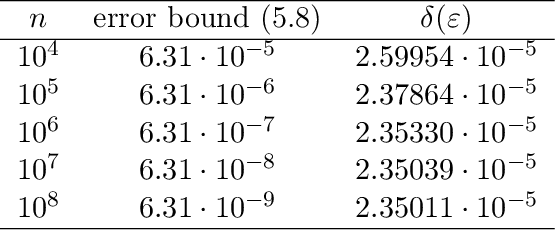
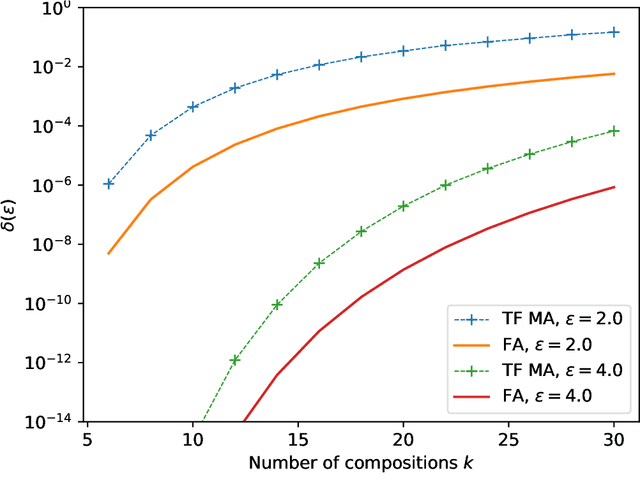
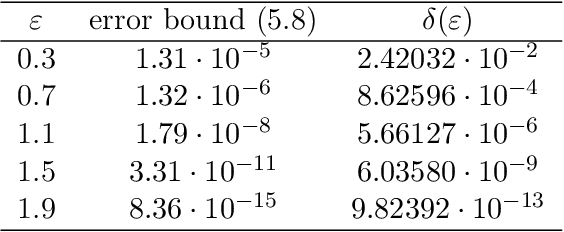
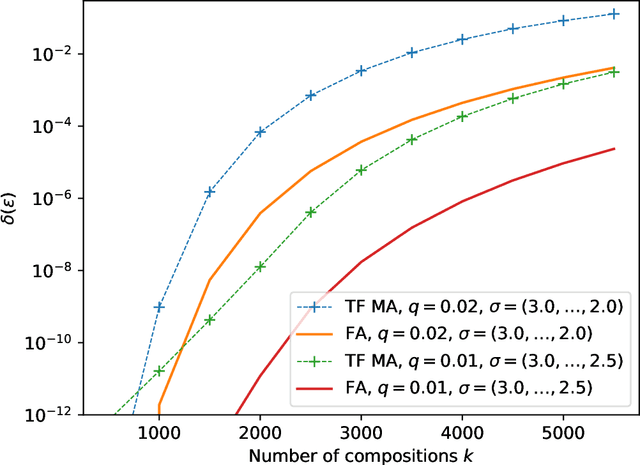
The recently proposed Fast Fourier Transform (FFT)-based accountant for evaluating $(\varepsilon,\delta)$-differential privacy guarantees using the privacy loss distribution formalism has been shown to give tighter bounds than commonly used methods such as R\'enyi accountants when applied to compositions of homogeneous mechanisms. This approach is also applicable to certain discrete mechanisms that cannot be analysed with R\'enyi accountants. In this paper, we extend this approach to compositions of heterogeneous mechanisms. We carry out a full error analysis that allows choosing the parameters of the algorithm such that a desired accuracy is obtained. Using our analysis, we also give a bound for the computational complexity in terms of the error which is analogous to and slightly tightens the one given by Murtagh and Vadhan (2018). We also show how to speed up the evaluation of tight privacy guarantees using the Plancherel theorem at the cost of increased pre-computation and memory usage.