Practical Differentially Private Hyperparameter Tuning with Subsampling
Paper and Code
Jan 27, 2023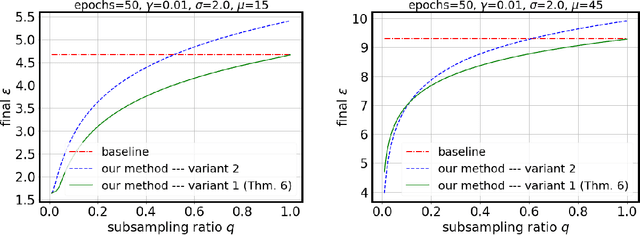

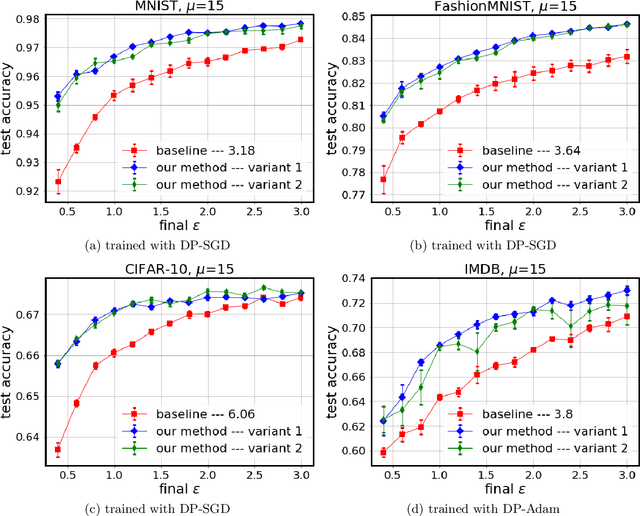

Tuning all the hyperparameters of differentially private (DP) machine learning (ML) algorithms often requires use of sensitive data and this may leak private information via hyperparameter values. Recently, Papernot and Steinke (2022) proposed a certain class of DP hyperparameter tuning algorithms, where the number of random search samples is randomized itself. Commonly, these algorithms still considerably increase the DP privacy parameter $\varepsilon$ over non-tuned DP ML model training and can be computationally heavy as evaluating each hyperparameter candidate requires a new training run. We focus on lowering both the DP bounds and the computational complexity of these methods by using only a random subset of the sensitive data for the hyperparameter tuning and by extrapolating the optimal values from the small dataset to a larger dataset. We provide a R\'enyi differential privacy analysis for the proposed method and experimentally show that it consistently leads to better privacy-utility trade-off than the baseline method by Papernot and Steinke (2022).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge