Tight Accounting in the Shuffle Model of Differential Privacy
Paper and Code
Jun 01, 2021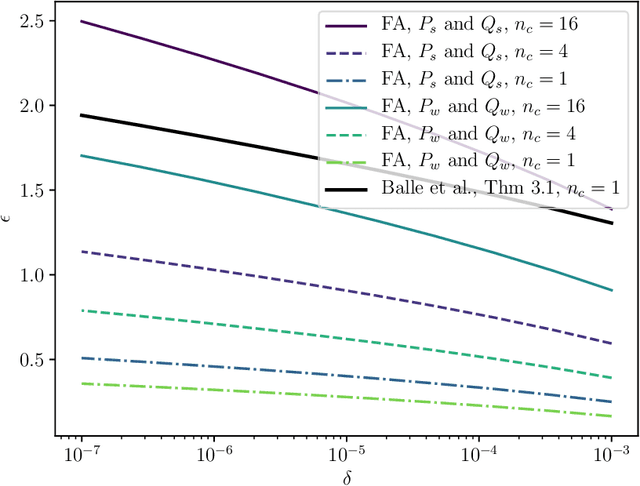
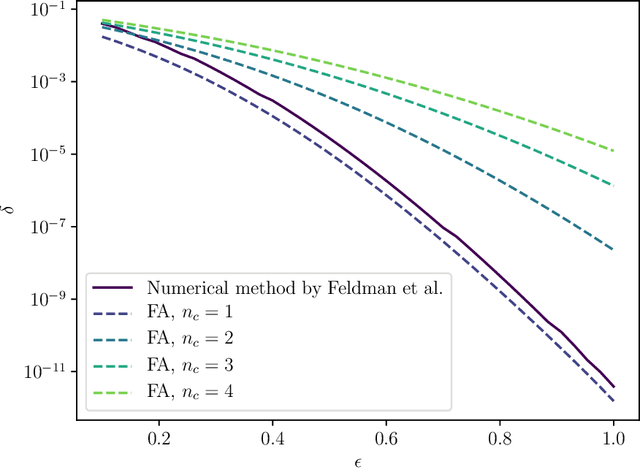
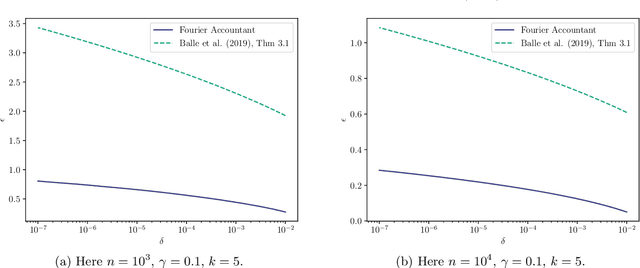
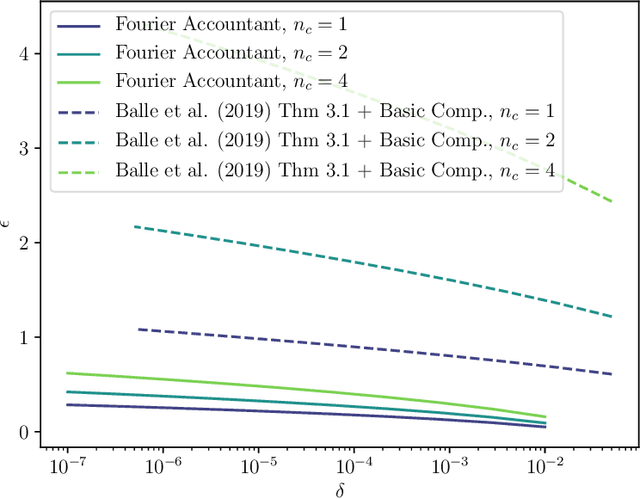
Shuffle model of differential privacy is a novel distributed privacy model based on a combination of local privacy mechanisms and a trusted shuffler. It has been shown that the additional randomisation provided by the shuffler improves privacy bounds compared to the purely local mechanisms. Accounting tight bounds, especially for multi-message protocols, is complicated by the complexity brought by the shuffler. The recently proposed Fourier Accountant for evaluating $(\varepsilon,\delta)$-differential privacy guarantees has been shown to give tighter bounds than commonly used methods for non-adaptive compositions of various complex mechanisms. In this paper we show how to compute tight privacy bounds using the Fourier Accountant for multi-message versions of several ubiquitous mechanisms in the shuffle model and demonstrate looseness of the existing bounds in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge