Differentially Private Convex Approximation of Two-Layer ReLU Networks
Paper and Code
Jul 05, 2024


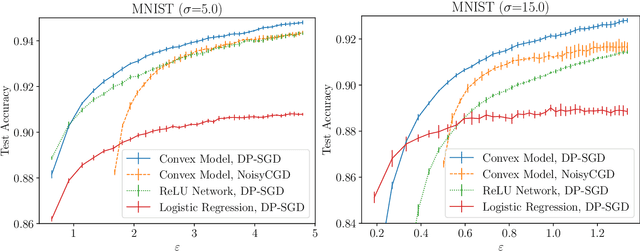
We show that it is possible to privately train convex problems that give models with similar privacy-utility trade-off as one hidden-layer ReLU networks trained with differentially private stochastic gradient descent (DP-SGD). As we show, this is possible via a certain dual formulation of the ReLU minimization problem. We derive a stochastic approximation of the dual problem that leads to a strongly convex problem which allows applying, for example, the privacy amplification by iteration type of analysis for gradient-based private optimizers, and in particular allows giving accurate privacy bounds for the noisy cyclic mini-batch gradient descent with fixed disjoint mini-batches. We obtain on the MNIST and FashionMNIST problems for the noisy cyclic mini-batch gradient descent first empirical results that show similar privacy-utility-trade-offs as DP-SGD applied to a ReLU network. We outline theoretical utility bounds that illustrate the speed-ups of the private convex approximation of ReLU networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge