Ground Reaction Force Estimation via Time-aware Knowledge Distillation

Human gait analysis with wearable sensors has been widely used in various applications, such as daily life healthcare, rehabilitation, physical therapy, and clinical diagnostics and monitoring. In particular, ground reaction force (GRF) provides critical information about how the body interacts with the ground during locomotion. Although instrumented treadmills have been widely used as the gold standard for measuring GRF during walking, their lack of portability and high cost make them impractical for many applications. As an alternative, low-cost, portable, wearable insole sensors have been utilized to measure GRF; however, these sensors are susceptible to noise and disturbance and are less accurate than treadmill measurements. To address these challenges, we propose a Time-aware Knowledge Distillation framework for GRF estimation from insole sensor data. This framework leverages similarity and temporal features within a mini-batch during the knowledge distillation process, effectively capturing the complementary relationships between features and the sequential properties of the target and input data. The performance of the lightweight models distilled through this framework was evaluated by comparing GRF estimations from insole sensor data against measurements from an instrumented treadmill. Empirical results demonstrated that Time-aware Knowledge Distillation outperforms current baselines in GRF estimation from wearable sensor data.

Intra-class Patch Swap for Self-Distillation

Knowledge distillation (KD) is a valuable technique for compressing large deep learning models into smaller, edge-suitable networks. However, conventional KD frameworks rely on pre-trained high-capacity teacher networks, which introduce significant challenges such as increased memory/storage requirements, additional training costs, and ambiguity in selecting an appropriate teacher for a given student model. Although a teacher-free distillation (self-distillation) has emerged as a promising alternative, many existing approaches still rely on architectural modifications or complex training procedures, which limit their generality and efficiency. To address these limitations, we propose a novel framework based on teacher-free distillation that operates using a single student network without any auxiliary components, architectural modifications, or additional learnable parameters. Our approach is built on a simple yet highly effective augmentation, called intra-class patch swap augmentation. This augmentation simulates a teacher-student dynamic within a single model by generating pairs of intra-class samples with varying confidence levels, and then applying instance-to-instance distillation to align their predictive distributions. Our method is conceptually simple, model-agnostic, and easy to implement, requiring only a single augmentation function. Extensive experiments across image classification, semantic segmentation, and object detection show that our method consistently outperforms both existing self-distillation baselines and conventional teacher-based KD approaches. These results suggest that the success of self-distillation could hinge on the design of the augmentation itself. Our codes are available at https://github.com/hchoi71/Intra-class-Patch-Swap.

Topological Persistence Guided Knowledge Distillation for Wearable Sensor Data

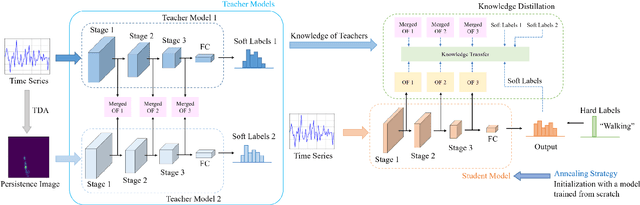
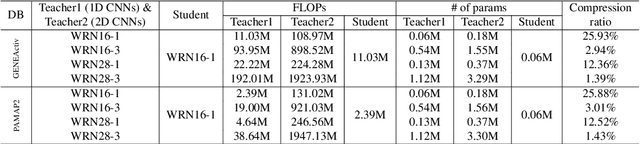
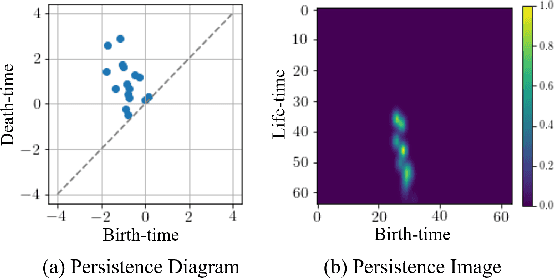
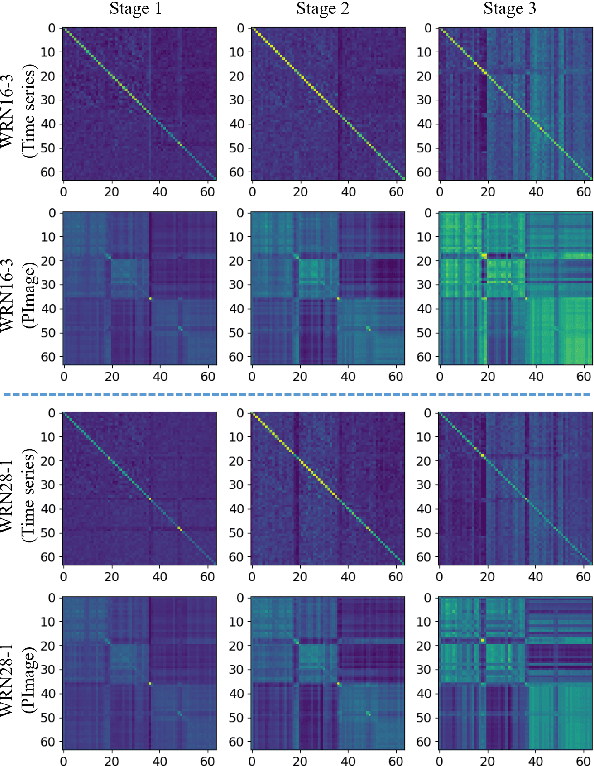
Deep learning methods have achieved a lot of success in various applications involving converting wearable sensor data to actionable health insights. A common application areas is activity recognition, where deep-learning methods still suffer from limitations such as sensitivity to signal quality, sensor characteristic variations, and variability between subjects. To mitigate these issues, robust features obtained by topological data analysis (TDA) have been suggested as a potential solution. However, there are two significant obstacles to using topological features in deep learning: (1) large computational load to extract topological features using TDA, and (2) different signal representations obtained from deep learning and TDA which makes fusion difficult. In this paper, to enable integration of the strengths of topological methods in deep-learning for time-series data, we propose to use two teacher networks, one trained on the raw time-series data, and another trained on persistence images generated by TDA methods. The distilled student model utilizes only the raw time-series data at test-time. This approach addresses both issues. The use of KD with multiple teachers utilizes complementary information, and results in a compact model with strong supervisory features and an integrated richer representation. To assimilate desirable information from different modalities, we design new constraints, including orthogonality imposed on feature correlation maps for improving feature expressiveness and allowing the student to easily learn from the teacher. Also, we apply an annealing strategy in KD for fast saturation and better accommodation from different features, while the knowledge gap between the teachers and student is reduced. Finally, a robust student model is distilled, which uses only the time-series data as an input, while implicitly preserving topological features.

Polynomial Implicit Neural Representations For Large Diverse Datasets

Implicit neural representations (INR) have gained significant popularity for signal and image representation for many end-tasks, such as superresolution, 3D modeling, and more. Most INR architectures rely on sinusoidal positional encoding, which accounts for high-frequency information in data. However, the finite encoding size restricts the model's representational power. Higher representational power is needed to go from representing a single given image to representing large and diverse datasets. Our approach addresses this gap by representing an image with a polynomial function and eliminates the need for positional encodings. Therefore, to achieve a progressively higher degree of polynomial representation, we use element-wise multiplications between features and affine-transformed coordinate locations after every ReLU layer. The proposed method is evaluated qualitatively and quantitatively on large datasets like ImageNet. The proposed Poly-INR model performs comparably to state-of-the-art generative models without any convolution, normalization, or self-attention layers, and with far fewer trainable parameters. With much fewer training parameters and higher representative power, our approach paves the way for broader adoption of INR models for generative modeling tasks in complex domains. The code is available at \url{https://github.com/Rajhans0/Poly_INR}

Leveraging Angular Distributions for Improved Knowledge Distillation

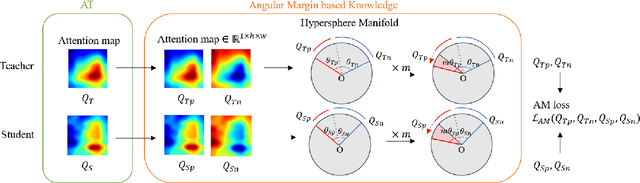
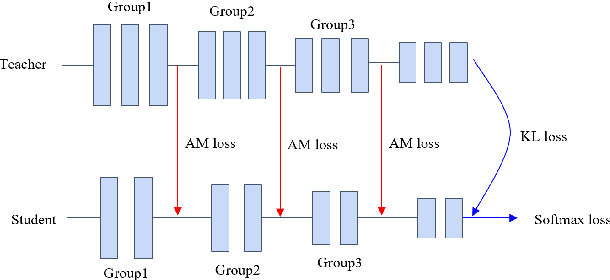
Knowledge distillation as a broad class of methods has led to the development of lightweight and memory efficient models, using a pre-trained model with a large capacity (teacher network) to train a smaller model (student network). Recently, additional variations for knowledge distillation, utilizing activation maps of intermediate layers as the source of knowledge, have been studied. Generally, in computer vision applications, it is seen that the feature activation learned by a higher capacity model contains richer knowledge, highlighting complete objects while focusing less on the background. Based on this observation, we leverage the dual ability of the teacher to accurately distinguish between positive (relevant to the target object) and negative (irrelevant) areas. We propose a new loss function for distillation, called angular margin-based distillation (AMD) loss. AMD loss uses the angular distance between positive and negative features by projecting them onto a hypersphere, motivated by the near angular distributions seen in many feature extractors. Then, we create a more attentive feature that is angularly distributed on the hypersphere by introducing an angular margin to the positive feature. Transferring such knowledge from the teacher network enables the student model to harness the higher discrimination of positive and negative features for the teacher, thus distilling superior student models. The proposed method is evaluated for various student-teacher network pairs on four public datasets. Furthermore, we show that the proposed method has advantages in compatibility with other learning techniques, such as using fine-grained features, augmentation, and other distillation methods.

Understanding the Role of Mixup in Knowledge Distillation: An Empirical Study

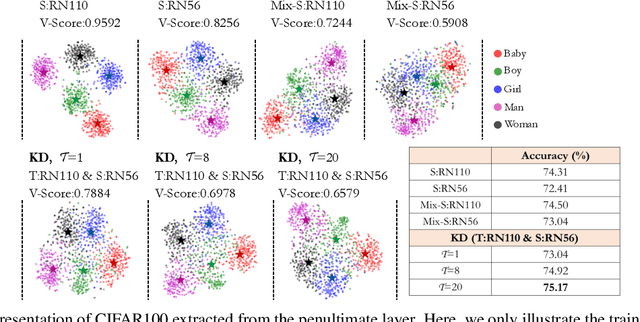
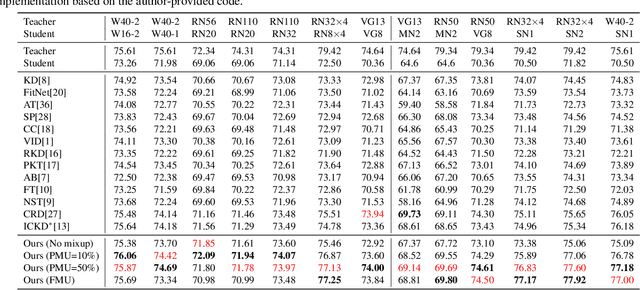
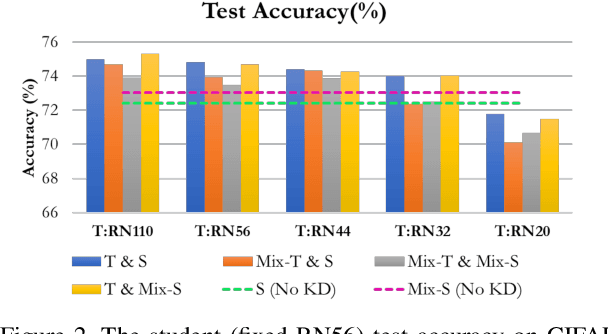
Mixup is a popular data augmentation technique based on creating new samples by linear interpolation between two given data samples, to improve both the generalization and robustness of the trained model. Knowledge distillation (KD), on the other hand, is widely used for model compression and transfer learning, which involves using a larger network's implicit knowledge to guide the learning of a smaller network. At first glance, these two techniques seem very different, however, we found that "smoothness" is the connecting link between the two and is also a crucial attribute in understanding KD's interplay with mixup. Although many mixup variants and distillation methods have been proposed, much remains to be understood regarding the role of a mixup in knowledge distillation. In this paper, we present a detailed empirical study on various important dimensions of compatibility between mixup and knowledge distillation. We also scrutinize the behavior of the networks trained with a mixup in the light of knowledge distillation through extensive analysis, visualizations, and comprehensive experiments on image classification. Finally, based on our findings, we suggest improved strategies to guide the student network to enhance its effectiveness. Additionally, the findings of this study provide insightful suggestions to researchers and practitioners that commonly use techniques from KD. Our code is available at https://github.com/hchoi71/MIX-KD.

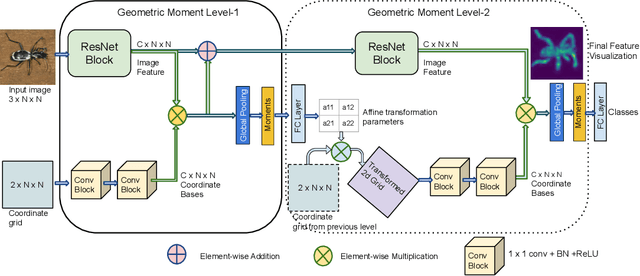
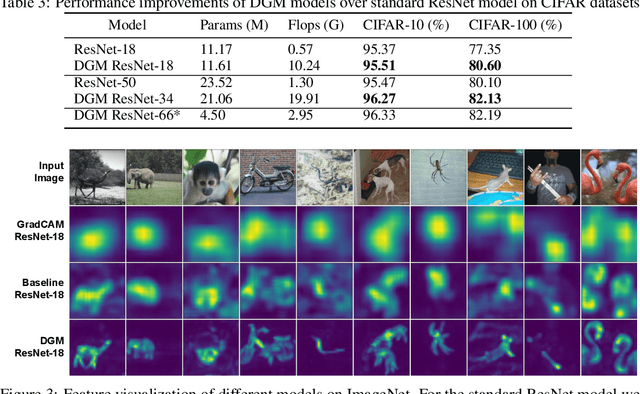
Deep Geometric Moment

Deep networks for image classification often rely more on texture information than object shape. While efforts have been made to make deep-models shape-aware, it is often difficult to make such models simple, interpretable, or rooted in known mathematical definitions of shape. This paper presents a deep-learning model inspired by geometric moments, a classically well understood approach to measure shape-related properties. The proposed method consists of a trainable network for generating coordinate bases and affine parameters for making the features geometrically invariant, yet in a task-specific manner. The proposed model improves the final feature's interpretation. We demonstrate the effectiveness of our method on standard image classification datasets. The proposed model achieves higher classification performance as compared to the baseline and standard ResNet models while substantially improving interpretability.

Role of Data Augmentation Strategies in Knowledge Distillation for Wearable Sensor Data

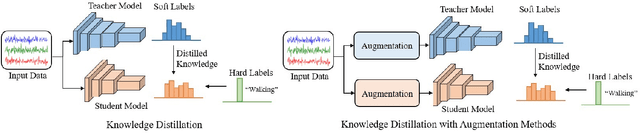
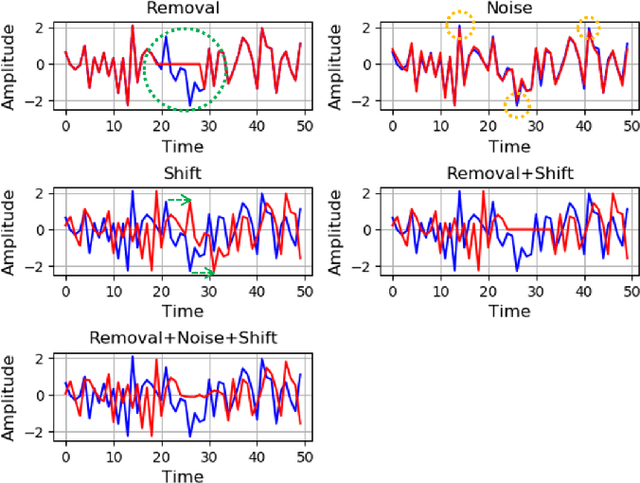
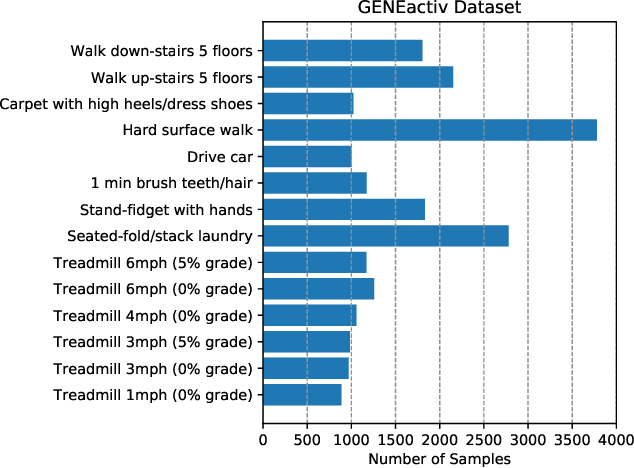
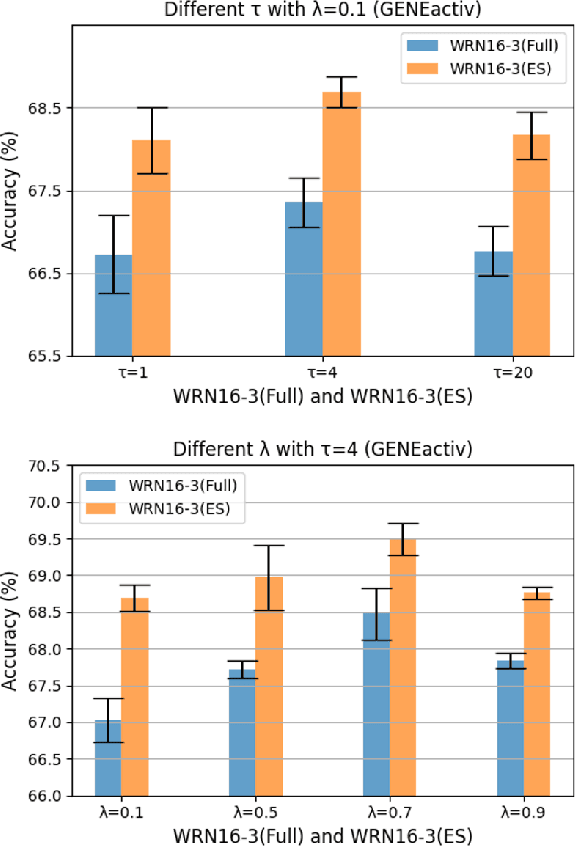
Deep neural networks are parametrized by several thousands or millions of parameters, and have shown tremendous success in many classification problems. However, the large number of parameters makes it difficult to integrate these models into edge devices such as smartphones and wearable devices. To address this problem, knowledge distillation (KD) has been widely employed, that uses a pre-trained high capacity network to train a much smaller network, suitable for edge devices. In this paper, for the first time, we study the applicability and challenges of using KD for time-series data for wearable devices. Successful application of KD requires specific choices of data augmentation methods during training. However, it is not yet known if there exists a coherent strategy for choosing an augmentation approach during KD. In this paper, we report the results of a detailed study that compares and contrasts various common choices and some hybrid data augmentation strategies in KD based human activity analysis. Research in this area is often limited as there are not many comprehensive databases available in the public domain from wearable devices. Our study considers databases from small scale publicly available to one derived from a large scale interventional study into human activity and sedentary behavior. We find that the choice of data augmentation techniques during KD have a variable level of impact on end performance, and find that the optimal network choice as well as data augmentation strategies are specific to a dataset at hand. However, we also conclude with a general set of recommendations that can provide a strong baseline performance across databases.

Geometric Priors for Scientific Generative Models in Inertial Confinement Fusion

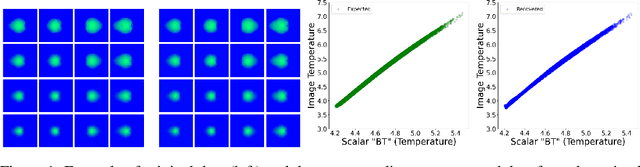
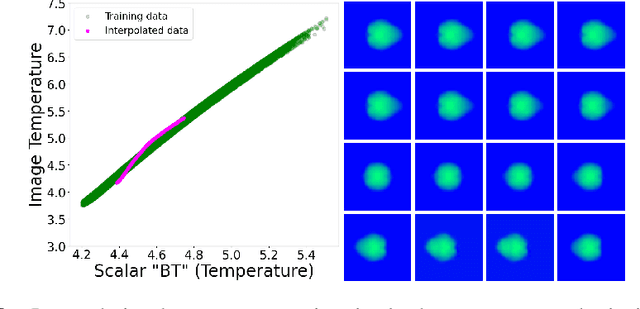
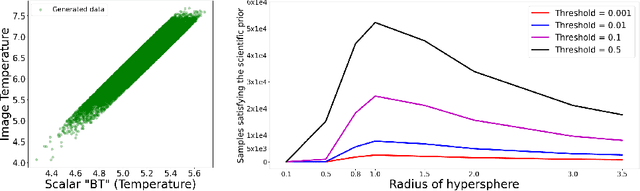
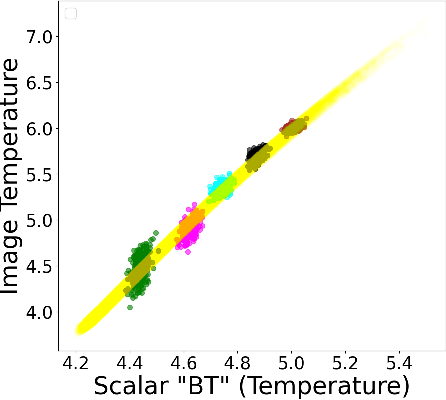
In this paper, we develop a Wasserstein autoencoder (WAE) with a hyperspherical prior for multimodal data in the application of inertial confinement fusion. Unlike a typical hyperspherical generative model that requires computationally inefficient sampling from distributions like the von Mis Fisher, we sample from a normal distribution followed by a projection layer before the generator. Finally, to determine the validity of the generated samples, we exploit a known relationship between the modalities in the dataset as a scientific constraint, and study different properties of the proposed model.

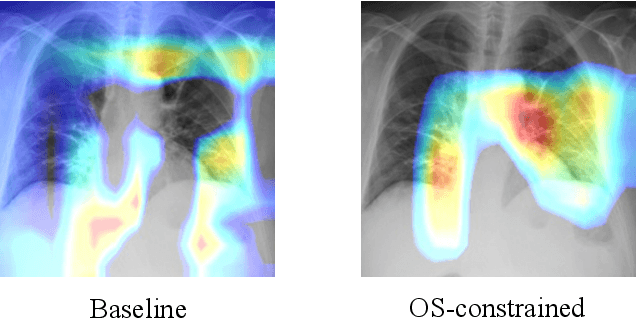
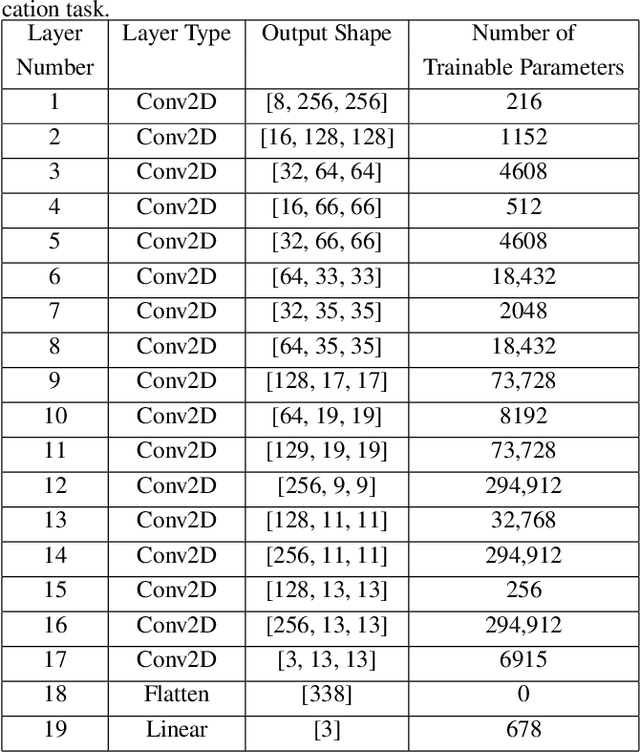
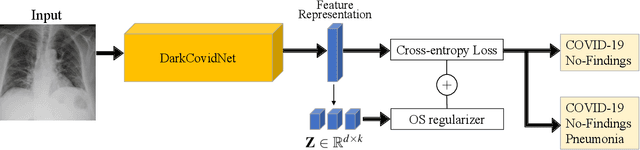
Interpretable COVID-19 Chest X-Ray Classification via Orthogonality Constraint

Deep neural networks have increasingly been used as an auxiliary tool in healthcare applications, due to their ability to improve performance of several diagnosis tasks. However, these methods are not widely adopted in clinical settings due to the practical limitations in the reliability, generalizability, and interpretability of deep learning based systems. As a result, methods have been developed that impose additional constraints during network training to gain more control as well as improve interpretabilty, facilitating their acceptance in healthcare community. In this work, we investigate the benefit of using Orthogonal Spheres (OS) constraint for classification of COVID-19 cases from chest X-ray images. The OS constraint can be written as a simple orthonormality term which is used in conjunction with the standard cross-entropy loss during classification network training. Previous studies have demonstrated significant benefits in applying such constraints to deep learning models. Our findings corroborate these observations, indicating that the orthonormality loss function effectively produces improved semantic localization via GradCAM visualizations, enhanced classification performance, and reduced model calibration error. Our approach achieves an improvement in accuracy of 1.6% and 4.8% for two- and three-class classification, respectively; similar results are found for models with data augmentation applied. In addition to these findings, our work also presents a new application of the OS regularizer in healthcare, increasing the post-hoc interpretability and performance of deep learning models for COVID-19 classification to facilitate adoption of these methods in clinical settings. We also identify the limitations of our strategy that can be explored for further research in future.