Brian K. Spears
Lawrence Livermore National Laboratory, Livermore, CA
Geometric Priors for Scientific Generative Models in Inertial Confinement Fusion
Nov 24, 2021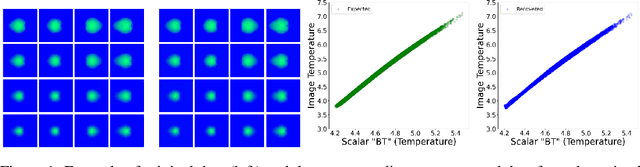
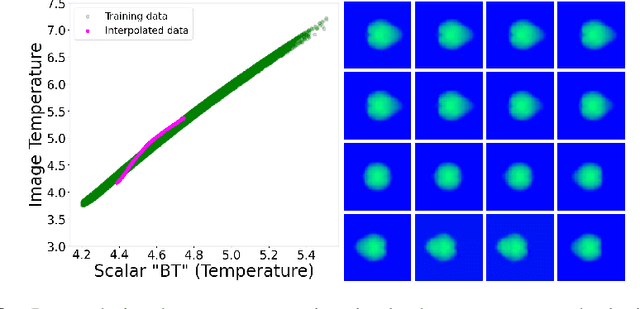
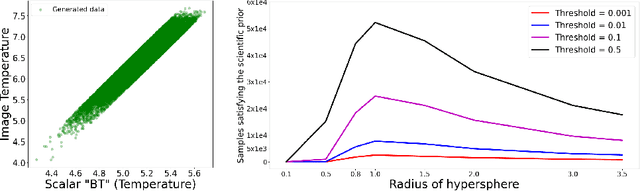
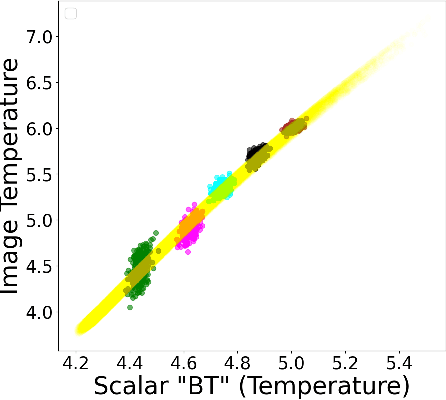
Abstract:In this paper, we develop a Wasserstein autoencoder (WAE) with a hyperspherical prior for multimodal data in the application of inertial confinement fusion. Unlike a typical hyperspherical generative model that requires computationally inefficient sampling from distributions like the von Mis Fisher, we sample from a normal distribution followed by a projection layer before the generator. Finally, to determine the validity of the generated samples, we exploit a known relationship between the modalities in the dataset as a scientific constraint, and study different properties of the proposed model.
Transfer learning suppresses simulation bias in predictive models built from sparse, multi-modal data
Apr 19, 2021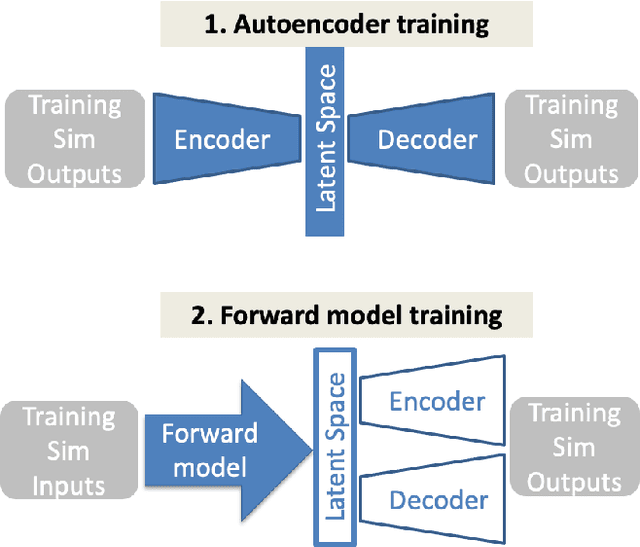
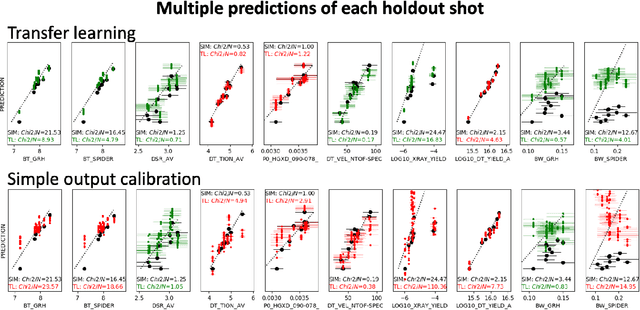
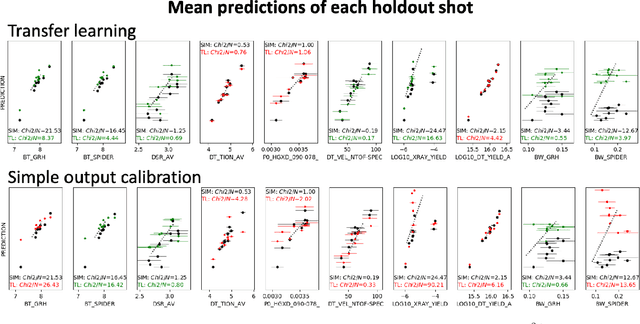
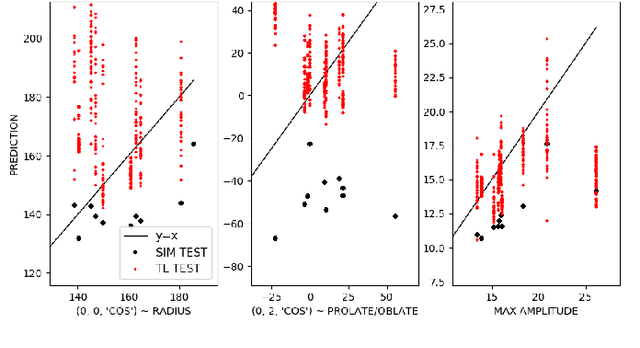
Abstract:Many problems in science, engineering, and business require making predictions based on very few observations. To build a robust predictive model, these sparse data may need to be augmented with simulated data, especially when the design space is multidimensional. Simulations, however, often suffer from an inherent bias. Estimation of this bias may be poorly constrained not only because of data sparsity, but also because traditional predictive models fit only one type of observations, such as scalars or images, instead of all available data modalities, which might have been acquired and simulated at great cost. We combine recent developments in deep learning to build more robust predictive models from multimodal data with a recent, novel technique to suppress the bias, and extend it to take into account multiple data modalities. First, an initial, simulation-trained, neural network surrogate model learns important correlations between different data modalities and between simulation inputs and outputs. Then, the model is partially retrained, or transfer learned, to fit the observations. Using fewer than 10 inertial confinement fusion experiments for retraining, we demonstrate that this technique systematically improves simulation predictions while a simple output calibration makes predictions worse. We also offer extensive cross-validation with real and synthetic data to support our findings. The transfer learning method can be applied to other problems that require transferring knowledge from simulations to the domain of real observations. This paper opens up the path to model calibration using multiple data types, which have traditionally been ignored in predictive models.
Meaningful uncertainties from deep neural network surrogates of large-scale numerical simulations
Oct 26, 2020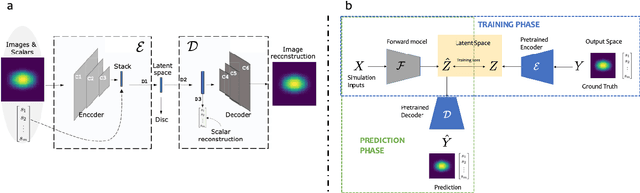
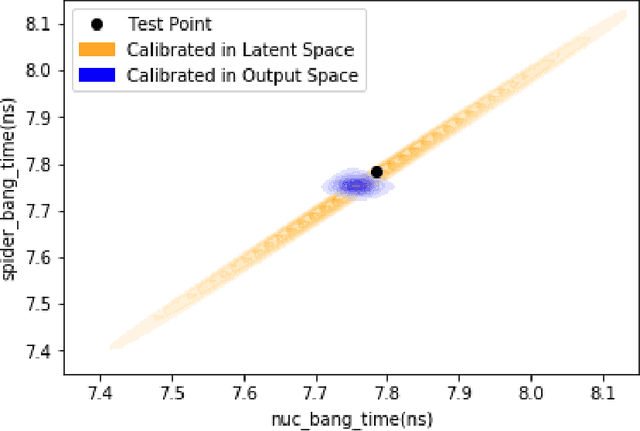
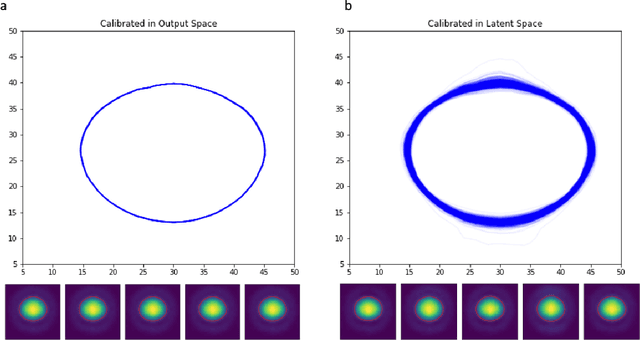
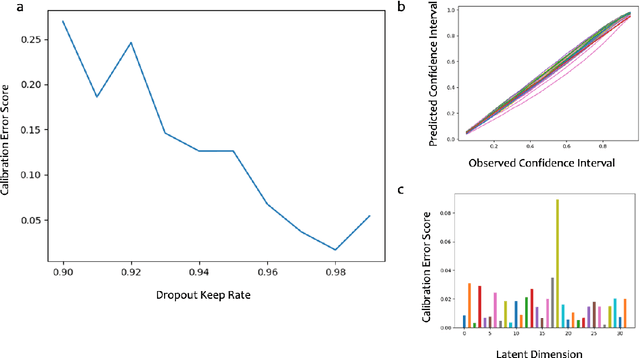
Abstract:Large-scale numerical simulations are used across many scientific disciplines to facilitate experimental development and provide insights into underlying physical processes, but they come with a significant computational cost. Deep neural networks (DNNs) can serve as highly-accurate surrogate models, with the capacity to handle diverse datatypes, offering tremendous speed-ups for prediction and many other downstream tasks. An important use-case for these surrogates is the comparison between simulations and experiments; prediction uncertainty estimates are crucial for making such comparisons meaningful, yet standard DNNs do not provide them. In this work we define the fundamental requirements for a DNN to be useful for scientific applications, and demonstrate a general variational inference approach to equip predictions of scalar and image data from a DNN surrogate model trained on inertial confinement fusion simulations with calibrated Bayesian uncertainties. Critically, these uncertainties are interpretable, meaningful and preserve physics-correlations in the predicted quantities.
Improved Surrogates in Inertial Confinement Fusion with Manifold and Cycle Consistencies
Dec 17, 2019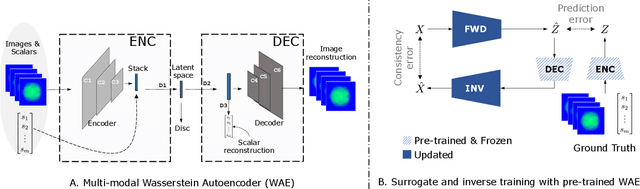

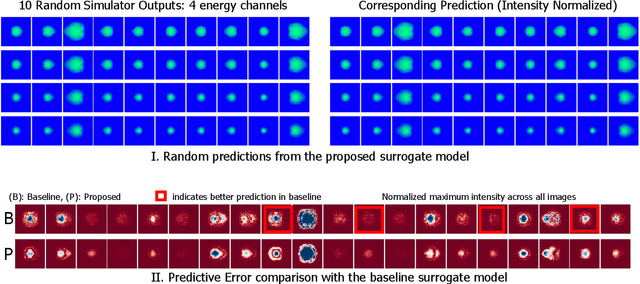
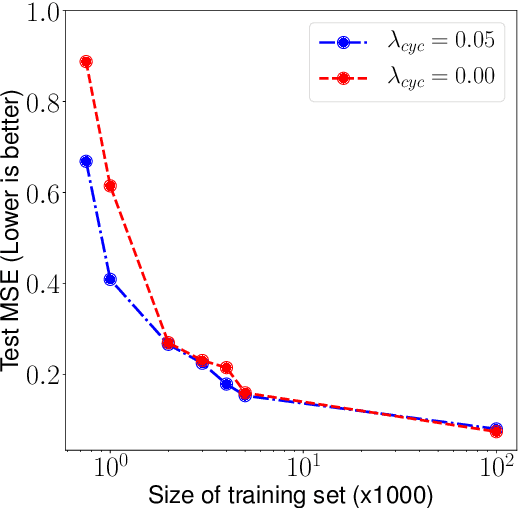
Abstract:Neural networks have become very popular in surrogate modeling because of their ability to characterize arbitrary, high dimensional functions in a data driven fashion. This paper advocates for the training of surrogates that are consistent with the physical manifold -- i.e., predictions are always physically meaningful, and are cyclically consistent -- i.e., when the predictions of the surrogate, when passed through an independently trained inverse model give back the original input parameters. We find that these two consistencies lead to surrogates that are superior in terms of predictive performance, more resilient to sampling artifacts, and tend to be more data efficient. Using Inertial Confinement Fusion (ICF) as a test bed problem, we model a 1D semi-analytic numerical simulator and demonstrate the effectiveness of our approach. Code and data are available at https://github.com/rushilanirudh/macc/
Exploring Generative Physics Models with Scientific Priors in Inertial Confinement Fusion
Oct 03, 2019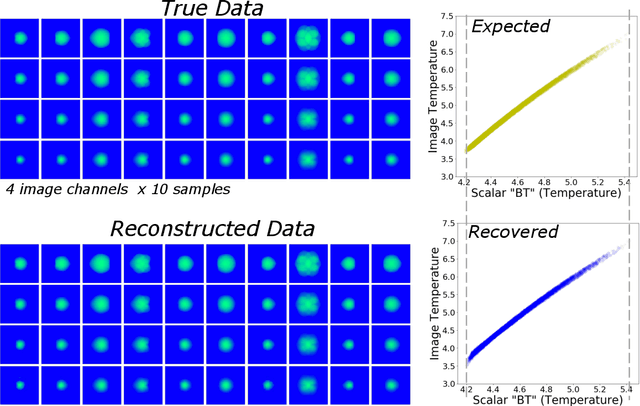
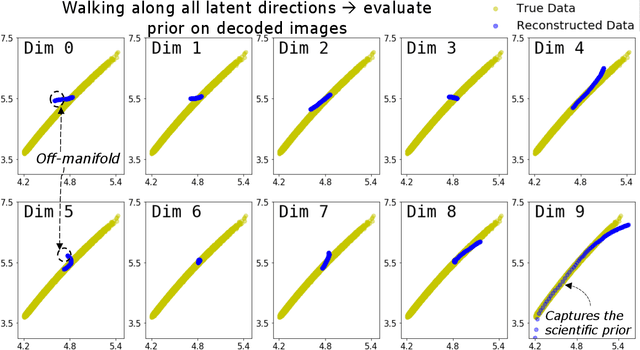
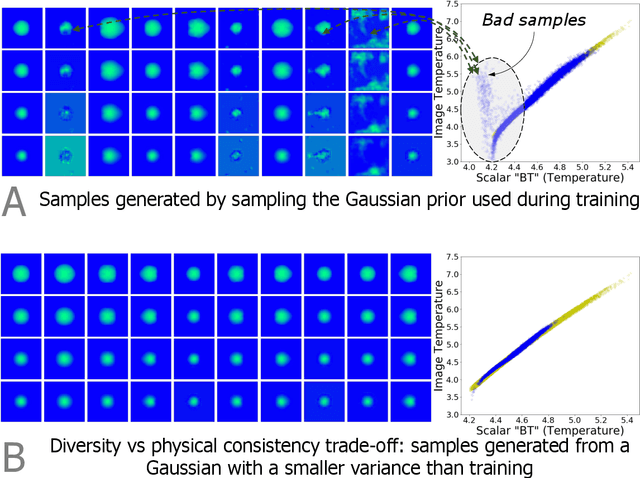
Abstract:There is significant interest in using modern neural networks for scientific applications due to their effectiveness in modeling highly complex, non-linear problems in a data-driven fashion. However, a common challenge is to verify the scientific plausibility or validity of outputs predicted by a neural network. This work advocates the use of known scientific constraints as a lens into evaluating, exploring, and understanding such predictions for the problem of inertial confinement fusion.
Scalable Topological Data Analysis and Visualization for Evaluating Data-Driven Models in Scientific Applications
Jul 19, 2019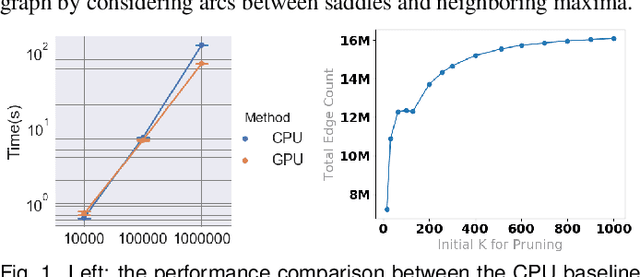
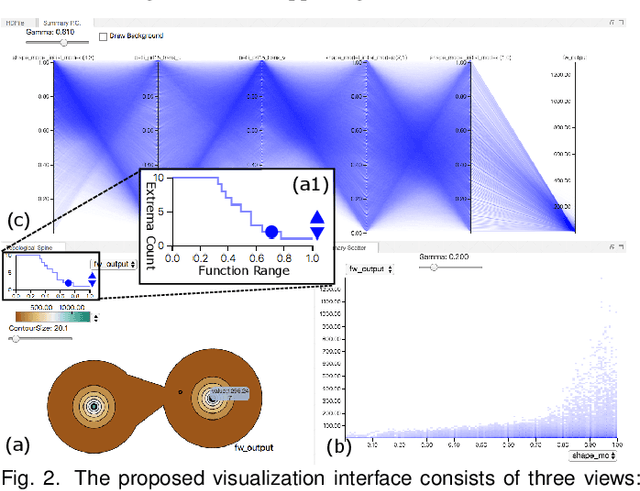
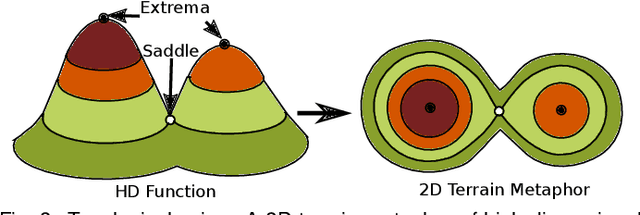
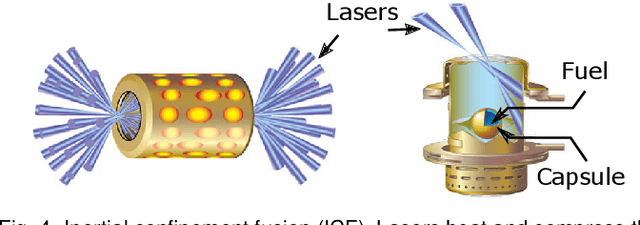
Abstract:With the rapid adoption of machine learning techniques for large-scale applications in science and engineering comes the convergence of two grand challenges in visualization. First, the utilization of black box models (e.g., deep neural networks) calls for advanced techniques in exploring and interpreting model behaviors. Second, the rapid growth in computing has produced enormous datasets that require techniques that can handle millions or more samples. Although some solutions to these interpretability challenges have been proposed, they typically do not scale beyond thousands of samples, nor do they provide the high-level intuition scientists are looking for. Here, we present the first scalable solution to explore and analyze high-dimensional functions often encountered in the scientific data analysis pipeline. By combining a new streaming neighborhood graph construction, the corresponding topology computation, and a novel data aggregation scheme, namely topology aware datacubes, we enable interactive exploration of both the topological and the geometric aspect of high-dimensional data. Following two use cases from high-energy-density (HED) physics and computational biology, we demonstrate how these capabilities have led to crucial new insights in both applications.
Contemporary machine learning: a guide for practitioners in the physical sciences
Dec 20, 2017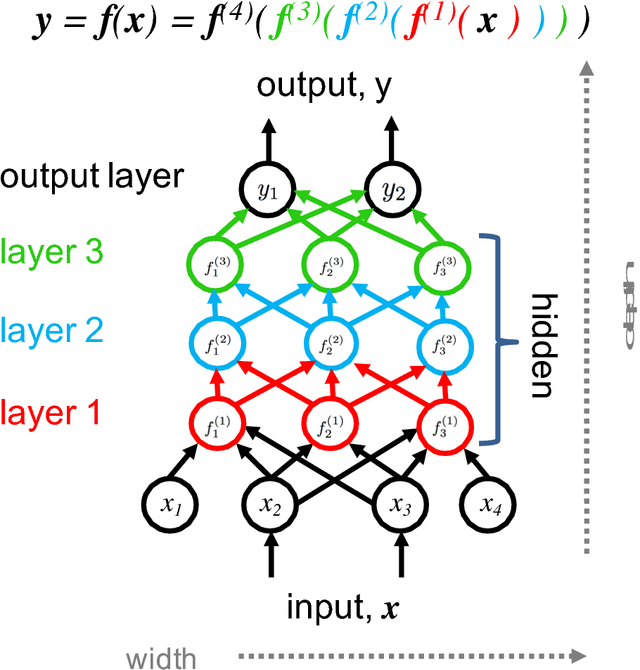
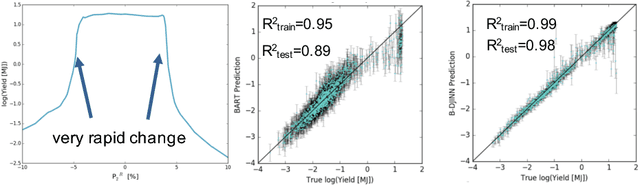
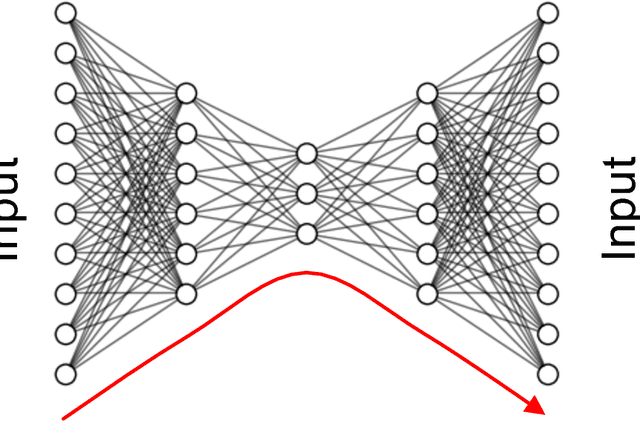
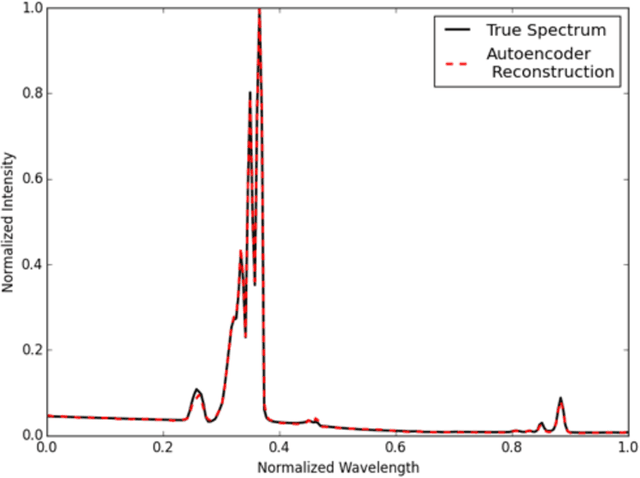
Abstract:Machine learning is finding increasingly broad application in the physical sciences. This most often involves building a model relationship between a dependent, measurable output and an associated set of controllable, but complicated, independent inputs. We present a tutorial on current techniques in machine learning -- a jumping-off point for interested researchers to advance their work. We focus on deep neural networks with an emphasis on demystifying deep learning. We begin with background ideas in machine learning and some example applications from current research in plasma physics. We discuss supervised learning techniques for modeling complicated functions, beginning with familiar regression schemes, then advancing to more sophisticated deep learning methods. We also address unsupervised learning and techniques for reducing the dimensionality of input spaces. Along the way, we describe methods for practitioners to help ensure that their models generalize from their training data to as-yet-unseen test data. We describe classes of tasks -- predicting scalars, handling images, fitting time-series -- and prepare the reader to choose an appropriate technique. We finally point out some limitations to modern machine learning and speculate on some ways that practitioners from the physical sciences may be particularly suited to help.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge