Learning thermodynamically constrained equations of state with uncertainty

Numerical simulations of high energy-density experiments require equation of state (EOS) models that relate a material's thermodynamic state variables -- specifically pressure, volume/density, energy, and temperature. EOS models are typically constructed using a semi-empirical parametric methodology, which assumes a physics-informed functional form with many tunable parameters calibrated using experimental/simulation data. Since there are inherent uncertainties in the calibration data (parametric uncertainty) and the assumed functional EOS form (model uncertainty), it is essential to perform uncertainty quantification (UQ) to improve confidence in the EOS predictions. Model uncertainty is challenging for UQ studies since it requires exploring the space of all possible physically consistent functional forms. Thus, it is often neglected in favor of parametric uncertainty, which is easier to quantify without violating thermodynamic laws. This work presents a data-driven machine learning approach to constructing EOS models that naturally captures model uncertainty while satisfying the necessary thermodynamic consistency and stability constraints. We propose a novel framework based on physics-informed Gaussian process regression (GPR) that automatically captures total uncertainty in the EOS and can be jointly trained on both simulation and experimental data sources. A GPR model for the shock Hugoniot is derived and its uncertainties are quantified using the proposed framework. We apply the proposed model to learn the EOS for the diamond solid state of carbon, using both density functional theory data and experimental shock Hugoniot data to train the model and show that the prediction uncertainty reduces by considering the thermodynamic constraints.

Transfer learning suppresses simulation bias in predictive models built from sparse, multi-modal data

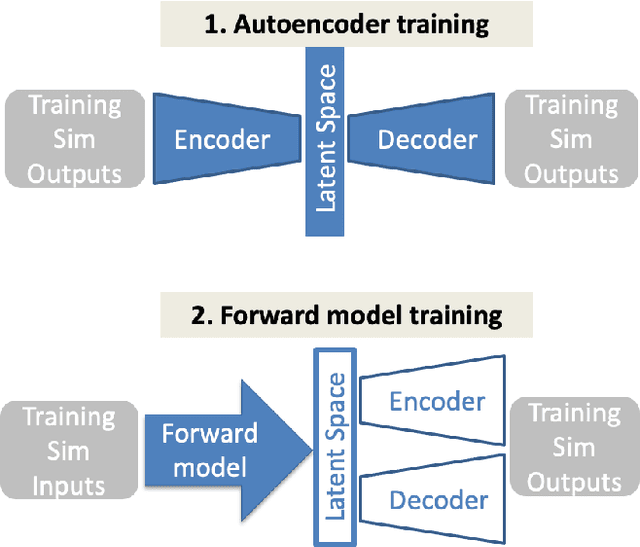
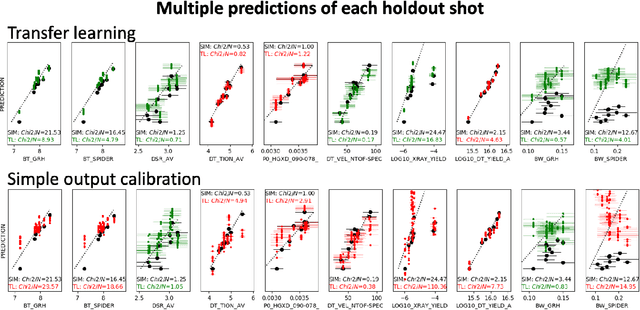
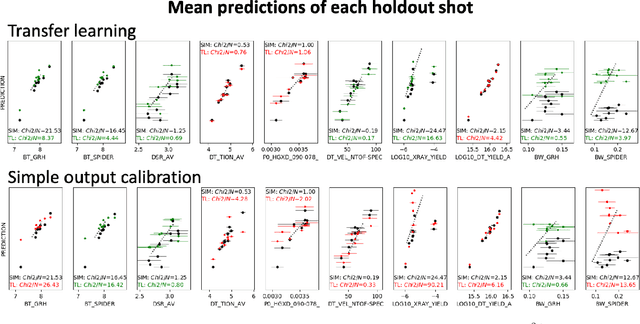
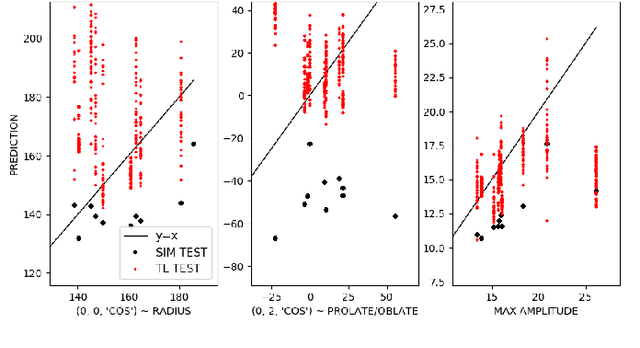
Many problems in science, engineering, and business require making predictions based on very few observations. To build a robust predictive model, these sparse data may need to be augmented with simulated data, especially when the design space is multidimensional. Simulations, however, often suffer from an inherent bias. Estimation of this bias may be poorly constrained not only because of data sparsity, but also because traditional predictive models fit only one type of observations, such as scalars or images, instead of all available data modalities, which might have been acquired and simulated at great cost. We combine recent developments in deep learning to build more robust predictive models from multimodal data with a recent, novel technique to suppress the bias, and extend it to take into account multiple data modalities. First, an initial, simulation-trained, neural network surrogate model learns important correlations between different data modalities and between simulation inputs and outputs. Then, the model is partially retrained, or transfer learned, to fit the observations. Using fewer than 10 inertial confinement fusion experiments for retraining, we demonstrate that this technique systematically improves simulation predictions while a simple output calibration makes predictions worse. We also offer extensive cross-validation with real and synthetic data to support our findings. The transfer learning method can be applied to other problems that require transferring knowledge from simulations to the domain of real observations. This paper opens up the path to model calibration using multiple data types, which have traditionally been ignored in predictive models.

Meaningful uncertainties from deep neural network surrogates of large-scale numerical simulations

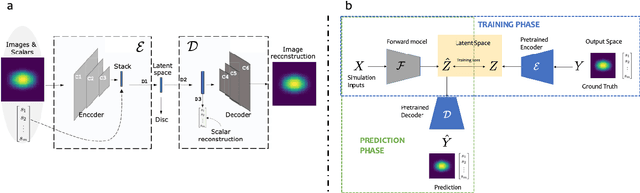
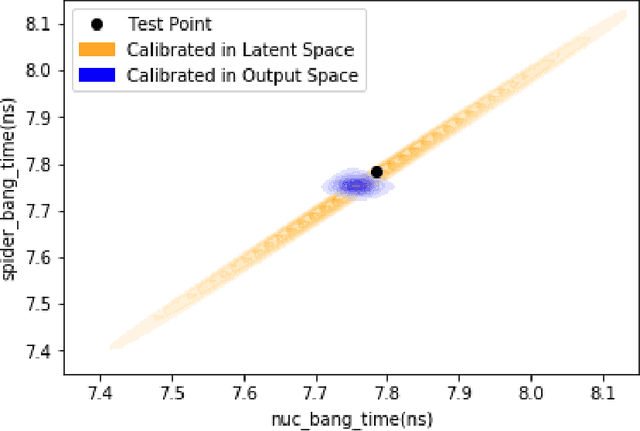
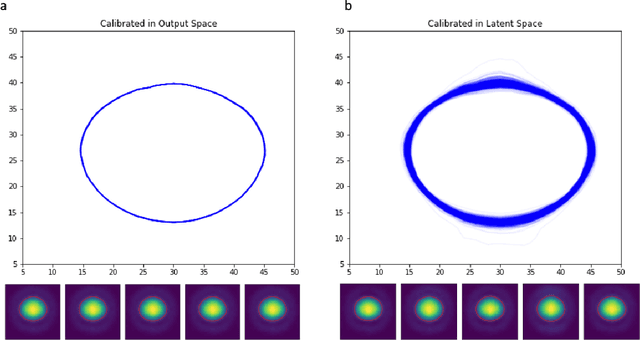
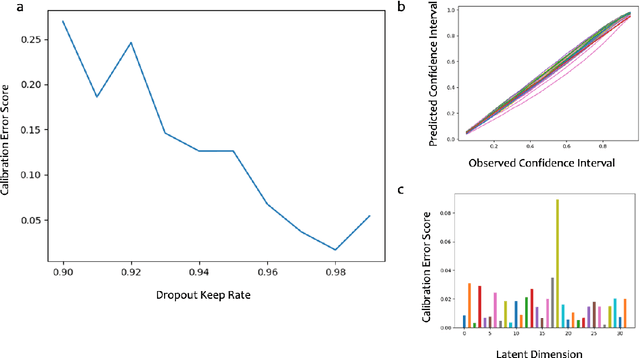
Large-scale numerical simulations are used across many scientific disciplines to facilitate experimental development and provide insights into underlying physical processes, but they come with a significant computational cost. Deep neural networks (DNNs) can serve as highly-accurate surrogate models, with the capacity to handle diverse datatypes, offering tremendous speed-ups for prediction and many other downstream tasks. An important use-case for these surrogates is the comparison between simulations and experiments; prediction uncertainty estimates are crucial for making such comparisons meaningful, yet standard DNNs do not provide them. In this work we define the fundamental requirements for a DNN to be useful for scientific applications, and demonstrate a general variational inference approach to equip predictions of scalar and image data from a DNN surrogate model trained on inertial confinement fusion simulations with calibrated Bayesian uncertainties. Critically, these uncertainties are interpretable, meaningful and preserve physics-correlations in the predicted quantities.

Merlin: Enabling Machine Learning-Ready HPC Ensembles

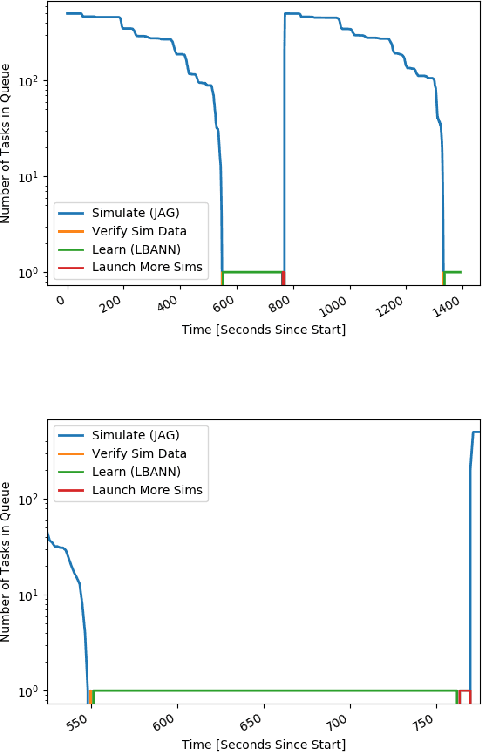
With the growing complexity of computational and experimental facilities, many scientific researchers are turning to machine learning (ML) techniques to analyze large scale ensemble data. With complexities such as multi-component workflows, heterogeneous machine architectures, parallel file systems, and batch scheduling, care must be taken to facilitate this analysis in a high performance computing (HPC) environment. In this paper, we present Merlin, a workflow framework to enable large ML-friendly ensembles of scientific HPC simulations. By augmenting traditional HPC with distributed compute technologies, Merlin aims to lower the barrier for scientific subject matter experts to incorporate ML into their analysis. In addition to its design and some examples, we describe how Merlin was deployed on the Sierra Supercomputer at Lawrence Livermore National Laboratory to create an unprecedented benchmark inertial confinement fusion dataset of approximately 100 million individual simulations and over 24 terabytes of multi-modal physics-based scalar, vector and hyperspectral image data.