Equation identification for fluid flows via physics-informed neural networks

Scientific machine learning (SciML) methods such as physics-informed neural networks (PINNs) are used to estimate parameters of interest from governing equations and small quantities of data. However, there has been little work in assessing how well PINNs perform for inverse problems across wide ranges of governing equations across the mathematical sciences. We present a new and challenging benchmark problem for inverse PINNs based on a parametric sweep of the 2D Burgers' equation with rotational flow. We show that a novel strategy that alternates between first- and second-order optimization proves superior to typical first-order strategies for estimating parameters. In addition, we propose a novel data-driven method to characterize PINN effectiveness in the inverse setting. PINNs' physics-informed regularization enables them to leverage small quantities of data more efficiently than the data-driven baseline. However, both PINNs and the baseline can fail to recover parameters for highly inviscid flows, motivating the need for further development of PINN methods.

Self-supervised learning for crystal property prediction via denoising

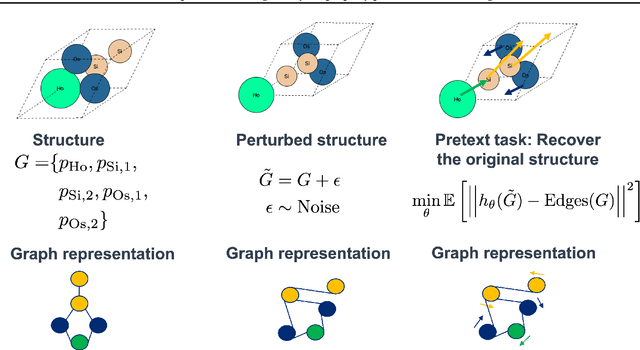
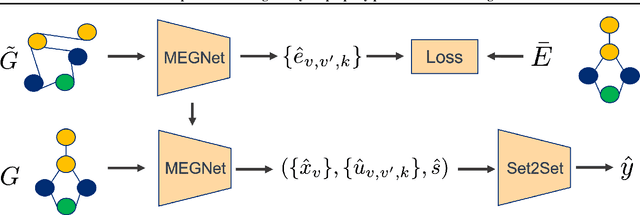
Accurate prediction of the properties of crystalline materials is crucial for targeted discovery, and this prediction is increasingly done with data-driven models. However, for many properties of interest, the number of materials for which a specific property has been determined is much smaller than the number of known materials. To overcome this disparity, we propose a novel self-supervised learning (SSL) strategy for material property prediction. Our approach, crystal denoising self-supervised learning (CDSSL), pretrains predictive models (e.g., graph networks) with a pretext task based on recovering valid material structures when given perturbed versions of these structures. We demonstrate that CDSSL models out-perform models trained without SSL, across material types, properties, and dataset sizes.

Data-efficient operator learning for solving high Mach number fluid flow problems

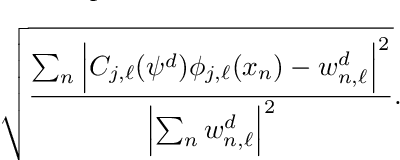
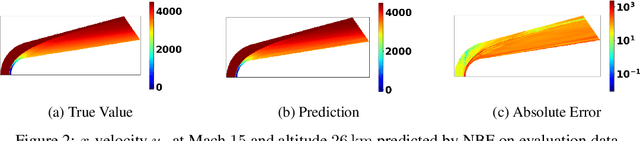
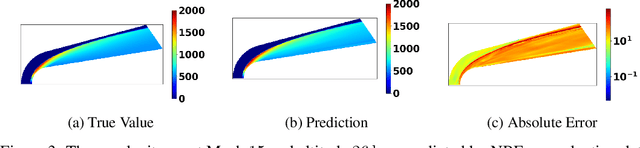
We consider the problem of using SciML to predict solutions of high Mach fluid flows over irregular geometries. In this setting, data is limited, and so it is desirable for models to perform well in the low-data setting. We show that Neural Basis Functions (NBF), which learns a basis of behavior modes from the data and then uses this basis to make predictions, is more effective than a basis-unaware baseline model. In addition, we identify continuing challenges in the space of predicting solutions for this type of problem.

Ensemble models outperform single model uncertainties and predictions for operator-learning of hypersonic flows

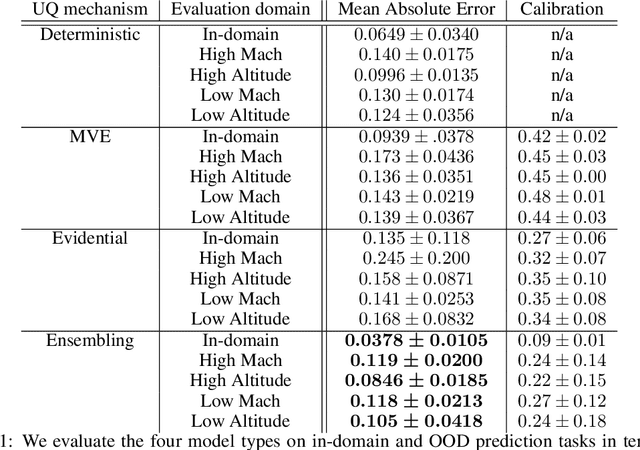
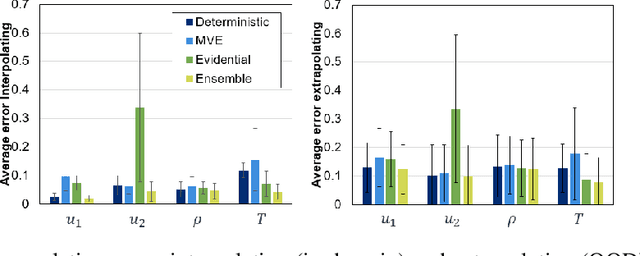
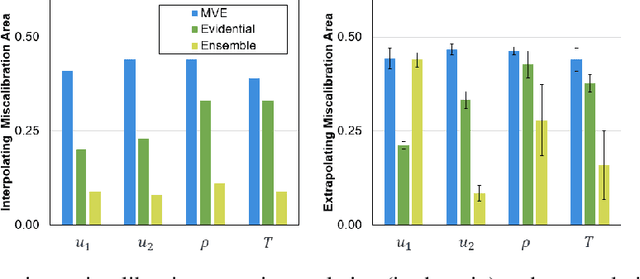
High-fidelity computational simulations and physical experiments of hypersonic flows are resource intensive. Training scientific machine learning (SciML) models on limited high-fidelity data offers one approach to rapidly predict behaviors for situations that have not been seen before. However, high-fidelity data is itself in limited quantity to validate all outputs of the SciML model in unexplored input space. As such, an uncertainty-aware SciML model is desired. The SciML model's output uncertainties could then be used to assess the reliability and confidence of the model's predictions. In this study, we extend a DeepONet using three different uncertainty quantification mechanisms: mean-variance estimation, evidential uncertainty, and ensembling. The uncertainty aware DeepONet models are trained and evaluated on the hypersonic flow around a blunt cone object with data generated via computational fluid dynamics over a wide range of Mach numbers and altitudes. We find that ensembling outperforms the other two uncertainty models in terms of minimizing error and calibrating uncertainty in both interpolative and extrapolative regimes.

A Domain-Agnostic Approach for Characterization of Lifelong Learning Systems

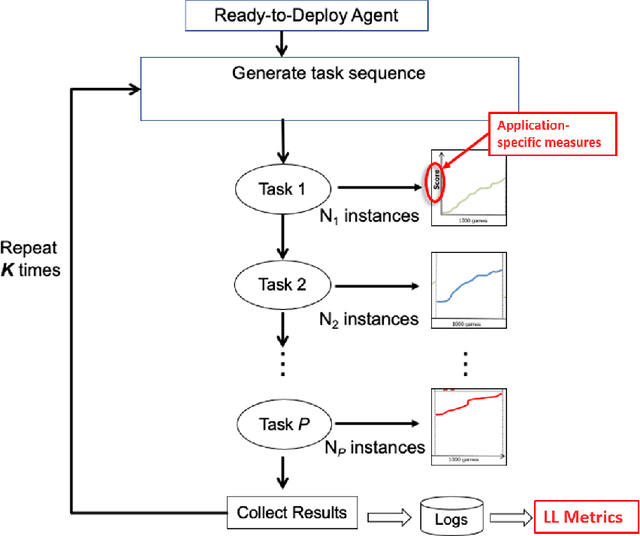
Despite the advancement of machine learning techniques in recent years, state-of-the-art systems lack robustness to "real world" events, where the input distributions and tasks encountered by the deployed systems will not be limited to the original training context, and systems will instead need to adapt to novel distributions and tasks while deployed. This critical gap may be addressed through the development of "Lifelong Learning" systems that are capable of 1) Continuous Learning, 2) Transfer and Adaptation, and 3) Scalability. Unfortunately, efforts to improve these capabilities are typically treated as distinct areas of research that are assessed independently, without regard to the impact of each separate capability on other aspects of the system. We instead propose a holistic approach, using a suite of metrics and an evaluation framework to assess Lifelong Learning in a principled way that is agnostic to specific domains or system techniques. Through five case studies, we show that this suite of metrics can inform the development of varied and complex Lifelong Learning systems. We highlight how the proposed suite of metrics quantifies performance trade-offs present during Lifelong Learning system development - both the widely discussed Stability-Plasticity dilemma and the newly proposed relationship between Sample Efficient and Robust Learning. Further, we make recommendations for the formulation and use of metrics to guide the continuing development of Lifelong Learning systems and assess their progress in the future.

Tunable Complexity Benchmarks for Evaluating Physics-Informed Neural Networks on Coupled Ordinary Differential Equations

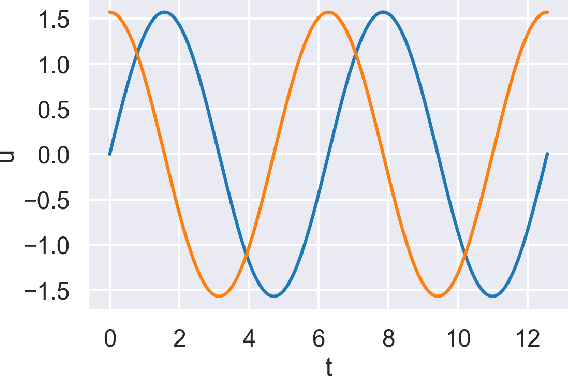
In this work, we assess the ability of physics-informed neural networks (PINNs) to solve increasingly-complex coupled ordinary differential equations (ODEs). We focus on a pair of benchmarks: discretized partial differential equations and harmonic oscillators, each of which has a tunable parameter that controls its complexity. Even by varying network architecture and applying a state-of-the-art training method that accounts for "difficult" training regions, we show that PINNs eventually fail to produce correct solutions to these benchmarks as their complexity -- the number of equations and the size of time domain -- increases. We identify several reasons why this may be the case, including insufficient network capacity, poor conditioning of the ODEs, and high local curvature, as measured by the Laplacian of the PINN loss.

Continual learning benefits from multiple sleep mechanisms: NREM, REM, and Synaptic Downscaling

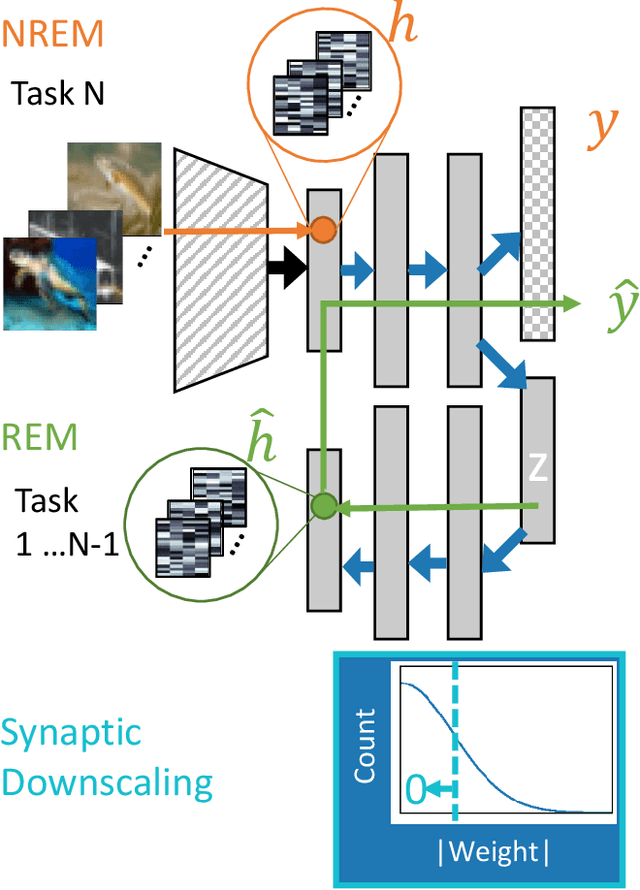
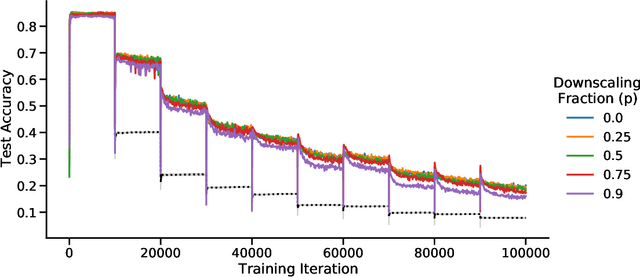
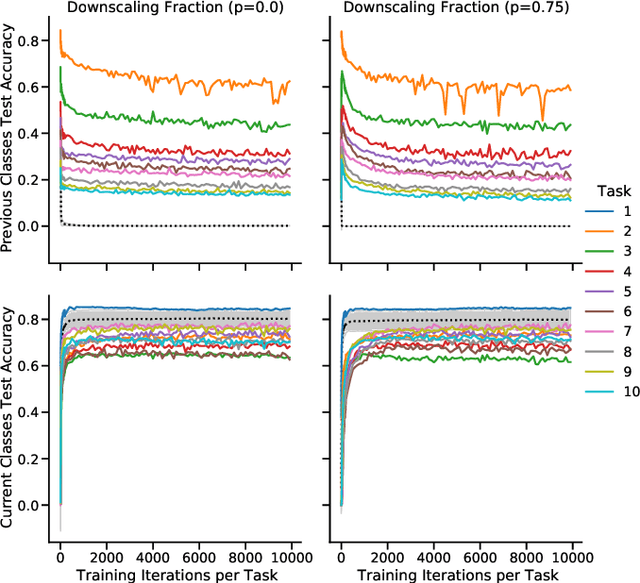
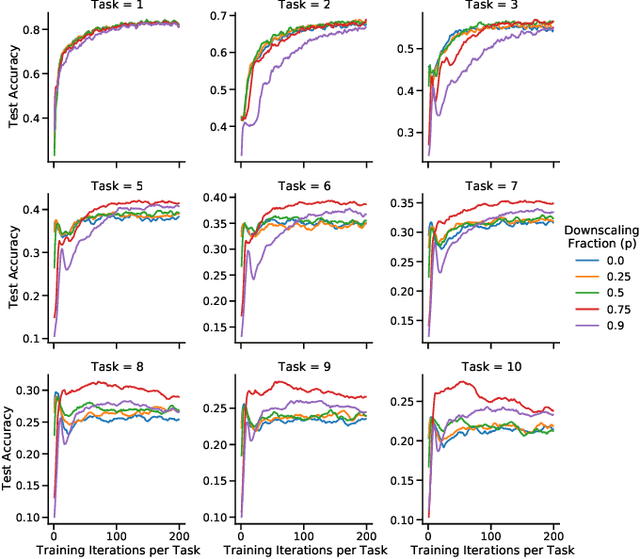
Learning new tasks and skills in succession without losing prior learning (i.e., catastrophic forgetting) is a computational challenge for both artificial and biological neural networks, yet artificial systems struggle to achieve parity with their biological analogues. Mammalian brains employ numerous neural operations in support of continual learning during sleep. These are ripe for artificial adaptation. Here, we investigate how modeling three distinct components of mammalian sleep together affects continual learning in artificial neural networks: (1) a veridical memory replay process observed during non-rapid eye movement (NREM) sleep; (2) a generative memory replay process linked to REM sleep; and (3) a synaptic downscaling process which has been proposed to tune signal-to-noise ratios and support neural upkeep. We find benefits from the inclusion of all three sleep components when evaluating performance on a continual learning CIFAR-100 image classification benchmark. Maximum accuracy improved during training and catastrophic forgetting was reduced during later tasks. While some catastrophic forgetting persisted over the course of network training, higher levels of synaptic downscaling lead to better retention of early tasks and further facilitated the recovery of early task accuracy during subsequent training. One key takeaway is that there is a trade-off at hand when considering the level of synaptic downscaling to use - more aggressive downscaling better protects early tasks, but less downscaling enhances the ability to learn new tasks. Intermediate levels can strike a balance with the highest overall accuracies during training. Overall, our results both provide insight into how to adapt sleep components to enhance artificial continual learning systems and highlight areas for future neuroscientific sleep research to further such systems.

Neural Basis Functions for Accelerating Solutions to High Mach Euler Equations

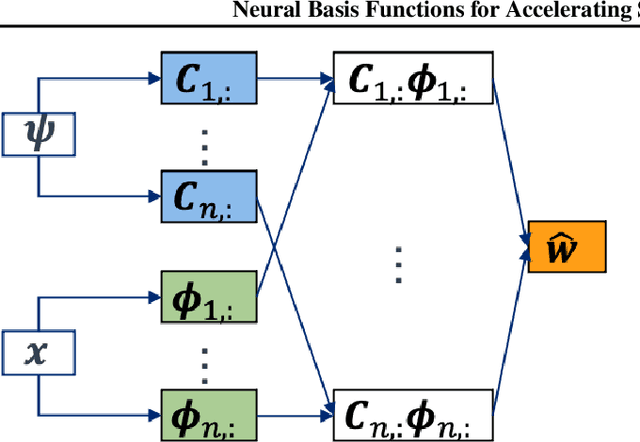
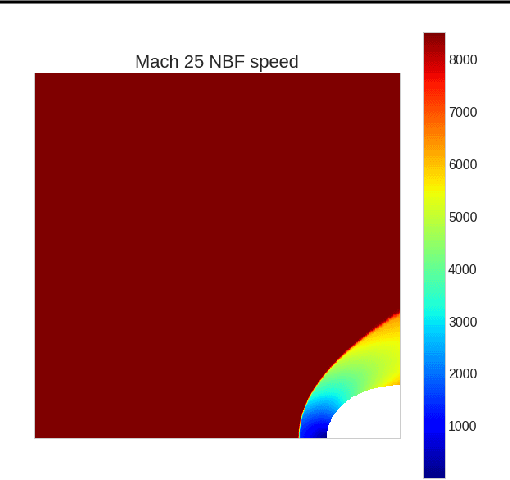
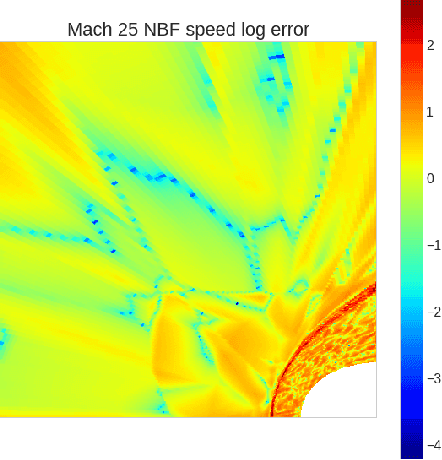
We propose an approach to solving partial differential equations (PDEs) using a set of neural networks which we call Neural Basis Functions (NBF). This NBF framework is a novel variation of the POD DeepONet operator learning approach where we regress a set of neural networks onto a reduced order Proper Orthogonal Decomposition (POD) basis. These networks are then used in combination with a branch network that ingests the parameters of the prescribed PDE to compute a reduced order approximation to the PDE. This approach is applied to the steady state Euler equations for high speed flow conditions (mach 10-30) where we consider the 2D flow around a cylinder which develops a shock condition. We then use the NBF predictions as initial conditions to a high fidelity Computational Fluid Dynamics (CFD) solver (CFD++) to show faster convergence. Lessons learned for training and implementing this algorithm will be presented as well.

Curvature-informed multi-task learning for graph networks

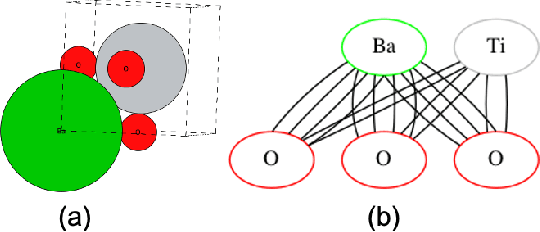
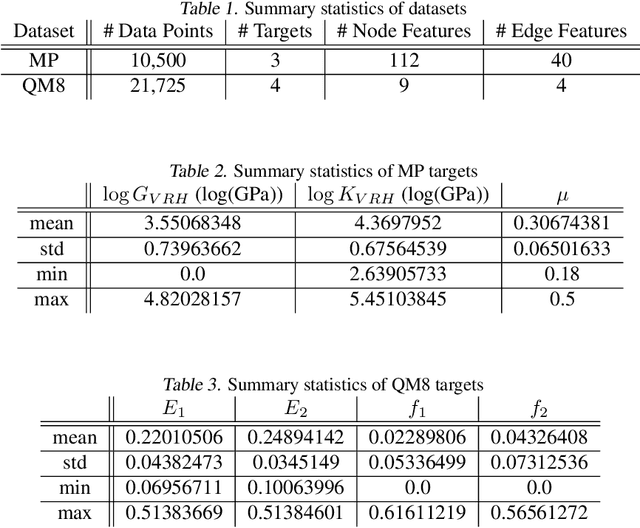
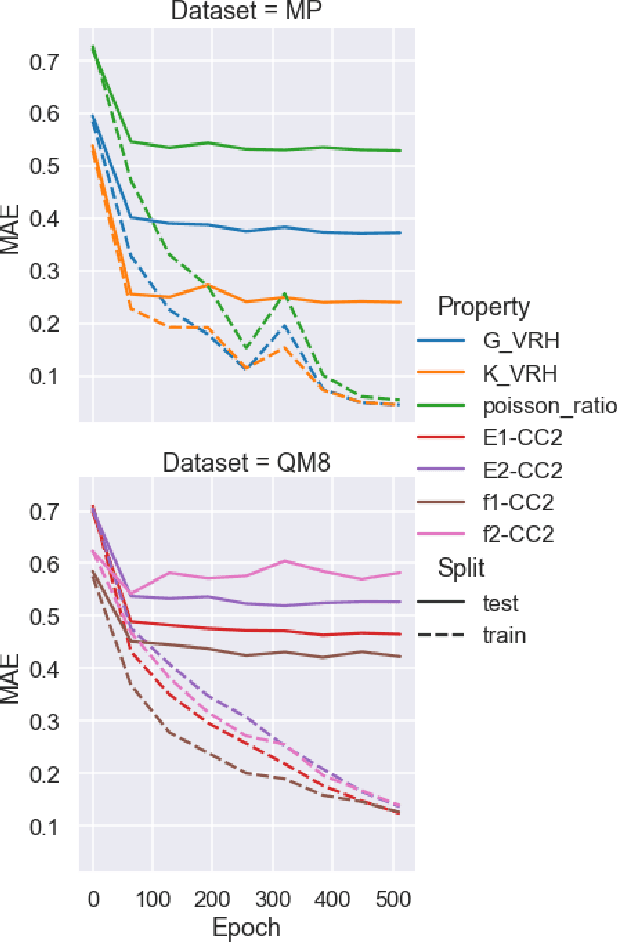
Properties of interest for crystals and molecules, such as band gap, elasticity, and solubility, are generally related to each other: they are governed by the same underlying laws of physics. However, when state-of-the-art graph neural networks attempt to predict multiple properties simultaneously (the multi-task learning (MTL) setting), they frequently underperform a suite of single property predictors. This suggests graph networks may not be fully leveraging these underlying similarities. Here we investigate a potential explanation for this phenomenon: the curvature of each property's loss surface significantly varies, leading to inefficient learning. This difference in curvature can be assessed by looking at spectral properties of the Hessians of each property's loss function, which is done in a matrix-free manner via randomized numerical linear algebra. We evaluate our hypothesis on two benchmark datasets (Materials Project (MP) and QM8) and consider how these findings can inform the training of novel multi-task learning models.

Latent Properties of Lifelong Learning Systems

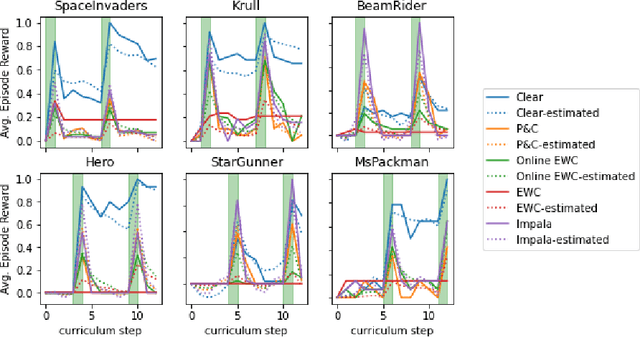
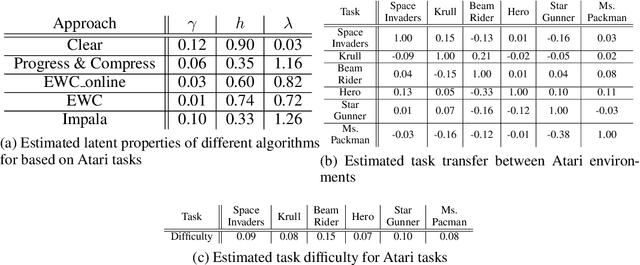
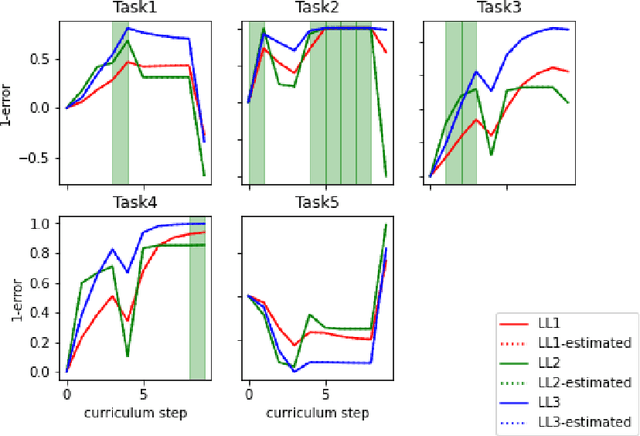
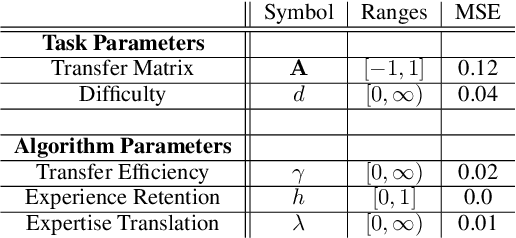
Creating artificial intelligence (AI) systems capable of demonstrating lifelong learning is a fundamental challenge, and many approaches and metrics have been proposed to analyze algorithmic properties. However, for existing lifelong learning metrics, algorithmic contributions are confounded by task and scenario structure. To mitigate this issue, we introduce an algorithm-agnostic explainable surrogate-modeling approach to estimate latent properties of lifelong learning algorithms. We validate the approach for estimating these properties via experiments on synthetic data. To validate the structure of the surrogate model, we analyze real performance data from a collection of popular lifelong learning approaches and baselines adapted for lifelong classification and lifelong reinforcement learning.