Tunable Complexity Benchmarks for Evaluating Physics-Informed Neural Networks on Coupled Ordinary Differential Equations

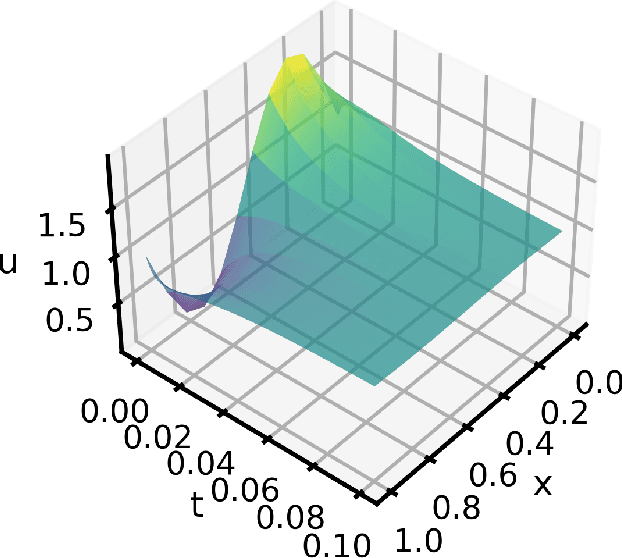
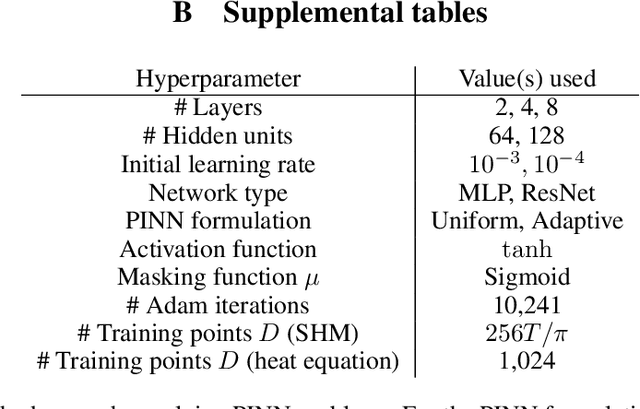
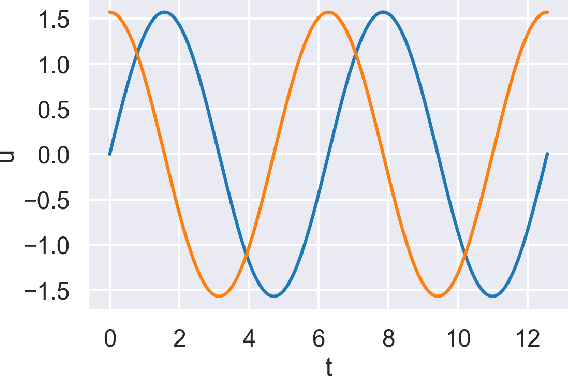
In this work, we assess the ability of physics-informed neural networks (PINNs) to solve increasingly-complex coupled ordinary differential equations (ODEs). We focus on a pair of benchmarks: discretized partial differential equations and harmonic oscillators, each of which has a tunable parameter that controls its complexity. Even by varying network architecture and applying a state-of-the-art training method that accounts for "difficult" training regions, we show that PINNs eventually fail to produce correct solutions to these benchmarks as their complexity -- the number of equations and the size of time domain -- increases. We identify several reasons why this may be the case, including insufficient network capacity, poor conditioning of the ODEs, and high local curvature, as measured by the Laplacian of the PINN loss.

Scatterbrained: A flexible and expandable pattern for decentralized machine learning

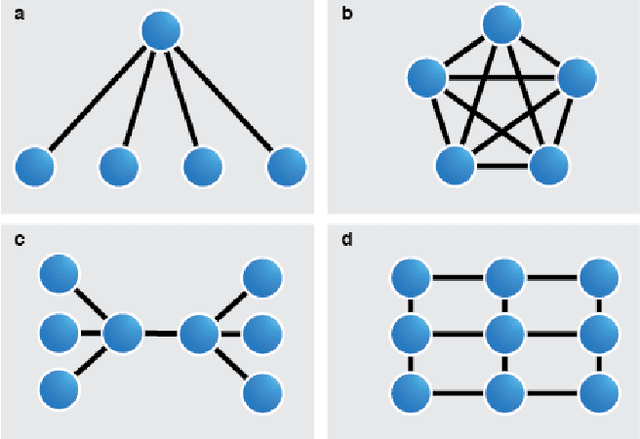
Federated machine learning is a technique for training a model across multiple devices without exchanging data between them. Because data remains local to each compute node, federated learning is well-suited for use-cases in fields where data is carefully controlled, such as medicine, or in domains with bandwidth constraints. One weakness of this approach is that most federated learning tools rely upon a central server to perform workload delegation and to produce a single shared model. Here, we suggest a flexible framework for decentralizing the federated learning pattern, and provide an open-source, reference implementation compatible with PyTorch.