James Schmidt
Taylor Learning
May 24, 2023
Abstract:Empirical risk minimization stands behind most optimization in supervised machine learning. Under this scheme, labeled data is used to approximate an expected cost (risk), and a learning algorithm updates model-defining parameters in search of an empirical risk minimizer, with the aim of thereby approximately minimizing expected cost. Parameter update is often done by some sort of gradient descent. In this paper, we introduce a learning algorithm to construct models for real analytic functions using neither gradient descent nor empirical risk minimization. Observing that such functions are defined by local information, we situate familiar Taylor approximation methods in the context of sampling data from a distribution, and prove a nonuniform learning result.
Testing for Overfitting
May 09, 2023



Abstract:High complexity models are notorious in machine learning for overfitting, a phenomenon in which models well represent data but fail to generalize an underlying data generating process. A typical procedure for circumventing overfitting computes empirical risk on a holdout set and halts once (or flags that/when) it begins to increase. Such practice often helps in outputting a well-generalizing model, but justification for why it works is primarily heuristic. We discuss the overfitting problem and explain why standard asymptotic and concentration results do not hold for evaluation with training data. We then proceed to introduce and argue for a hypothesis test by means of which both model performance may be evaluated using training data, and overfitting quantitatively defined and detected. We rely on said concentration bounds which guarantee that empirical means should, with high probability, approximate their true mean to conclude that they should approximate each other. We stipulate conditions under which this test is valid, describe how the test may be used for identifying overfitting, articulate a further nuance according to which distributional shift may be flagged, and highlight an alternative notion of learning which usefully captures generalization in the absence of uniform PAC guarantees.
Latent Properties of Lifelong Learning Systems
Jul 28, 2022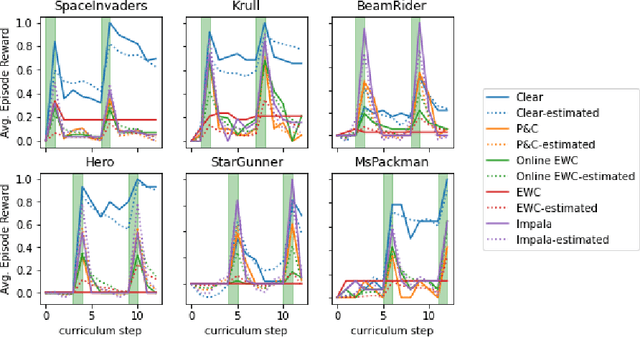
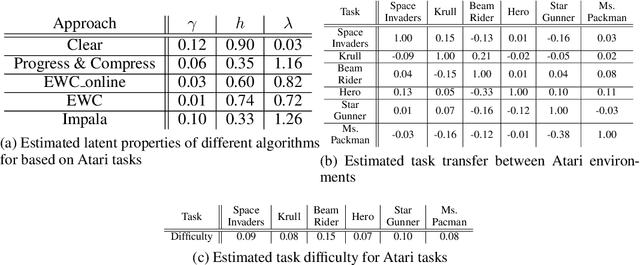
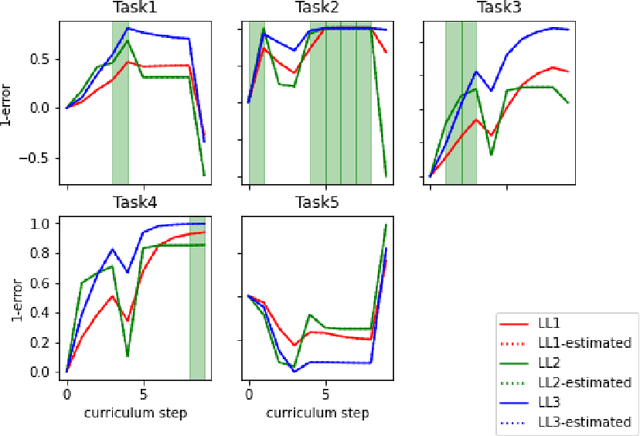
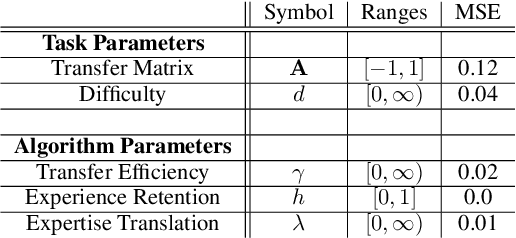
Abstract:Creating artificial intelligence (AI) systems capable of demonstrating lifelong learning is a fundamental challenge, and many approaches and metrics have been proposed to analyze algorithmic properties. However, for existing lifelong learning metrics, algorithmic contributions are confounded by task and scenario structure. To mitigate this issue, we introduce an algorithm-agnostic explainable surrogate-modeling approach to estimate latent properties of lifelong learning algorithms. We validate the approach for estimating these properties via experiments on synthetic data. To validate the structure of the surrogate model, we analyze real performance data from a collection of popular lifelong learning approaches and baselines adapted for lifelong classification and lifelong reinforcement learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge