Neural Basis Functions for Accelerating Solutions to High Mach Euler Equations
Paper and Code
Aug 02, 2022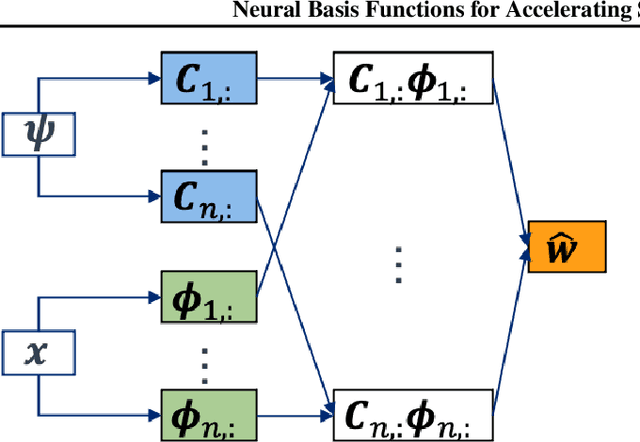
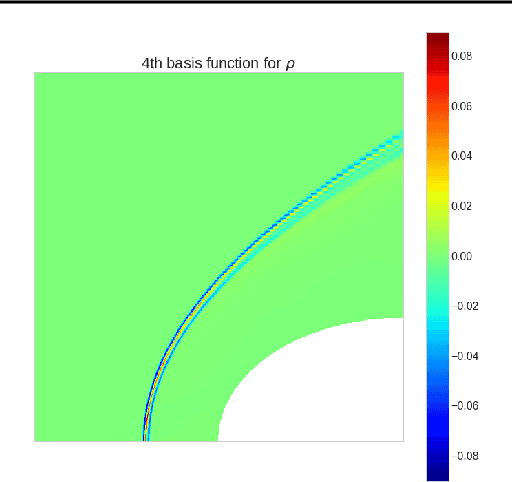
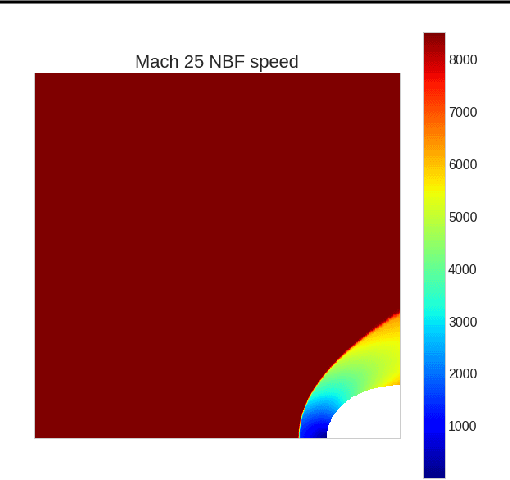
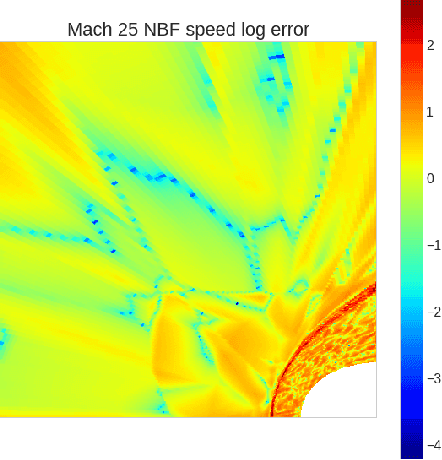
We propose an approach to solving partial differential equations (PDEs) using a set of neural networks which we call Neural Basis Functions (NBF). This NBF framework is a novel variation of the POD DeepONet operator learning approach where we regress a set of neural networks onto a reduced order Proper Orthogonal Decomposition (POD) basis. These networks are then used in combination with a branch network that ingests the parameters of the prescribed PDE to compute a reduced order approximation to the PDE. This approach is applied to the steady state Euler equations for high speed flow conditions (mach 10-30) where we consider the 2D flow around a cylinder which develops a shock condition. We then use the NBF predictions as initial conditions to a high fidelity Computational Fluid Dynamics (CFD) solver (CFD++) to show faster convergence. Lessons learned for training and implementing this algorithm will be presented as well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge