Janna Domenico
Curvature-informed multi-task learning for graph networks
Aug 02, 2022
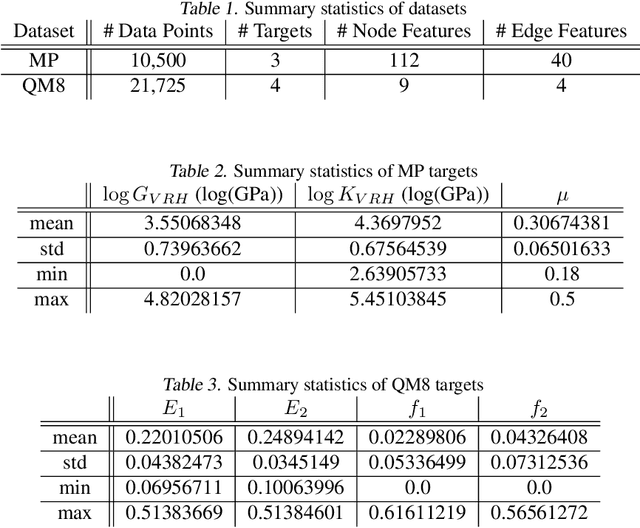
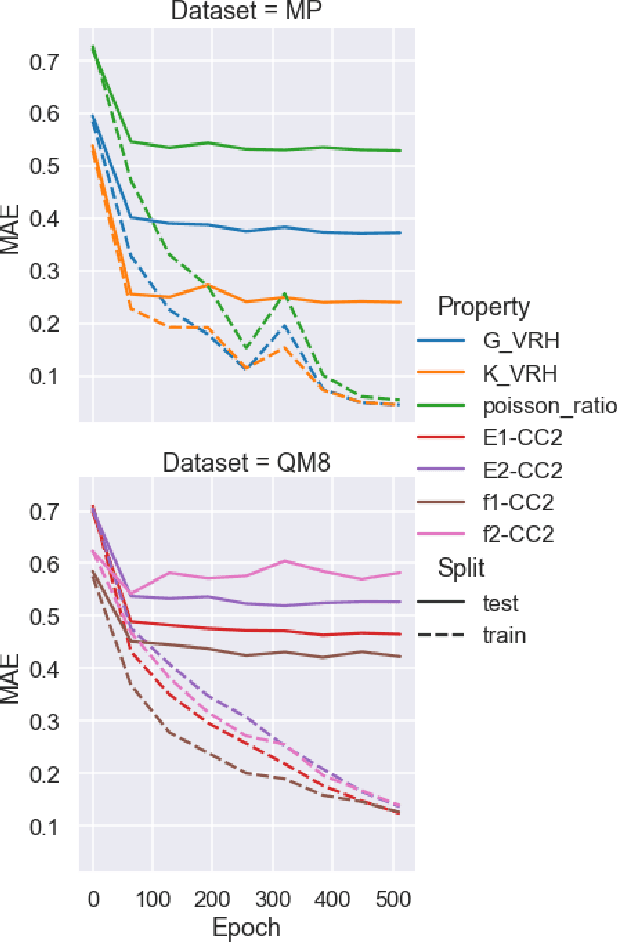
Abstract:Properties of interest for crystals and molecules, such as band gap, elasticity, and solubility, are generally related to each other: they are governed by the same underlying laws of physics. However, when state-of-the-art graph neural networks attempt to predict multiple properties simultaneously (the multi-task learning (MTL) setting), they frequently underperform a suite of single property predictors. This suggests graph networks may not be fully leveraging these underlying similarities. Here we investigate a potential explanation for this phenomenon: the curvature of each property's loss surface significantly varies, leading to inefficient learning. This difference in curvature can be assessed by looking at spectral properties of the Hessians of each property's loss function, which is done in a matrix-free manner via randomized numerical linear algebra. We evaluate our hypothesis on two benchmark datasets (Materials Project (MP) and QM8) and consider how these findings can inform the training of novel multi-task learning models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge