Alan J. X. Guo
Rethinking the Mean Teacher Strategy from the Perspective of Self-paced Learning
May 16, 2025



Abstract:Semi-supervised medical image segmentation has attracted significant attention due to its potential to reduce manual annotation costs. The mean teacher (MT) strategy, commonly understood as introducing smoothed, temporally lagged consistency regularization, has demonstrated strong performance across various tasks in this field. In this work, we reinterpret the MT strategy on supervised data as a form of self-paced learning, regulated by the output agreement between the temporally lagged teacher model and the ground truth labels. This idea is further extended to incorporate agreement between a temporally lagged model and a cross-architectural model, which offers greater flexibility in regulating the learning pace and enables application to unlabeled data. Specifically, we propose dual teacher-student learning (DTSL), a framework that introduces two groups of teacher-student models with different architectures. The output agreement between the cross-group teacher and student models is used as pseudo-labels, generated via a Jensen-Shannon divergence-based consensus label generator (CLG). Extensive experiments on popular datasets demonstrate that the proposed method consistently outperforms existing state-of-the-art approaches. Ablation studies further validate the effectiveness of the proposed modules.
Efficient Transformer-based Decoder for Varshamov-Tenengolts Codes
Feb 28, 2025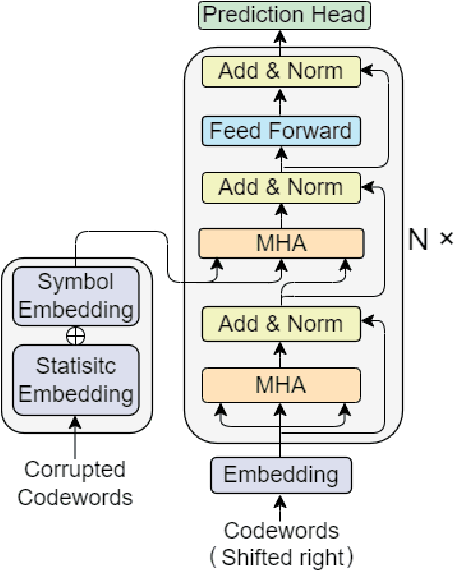
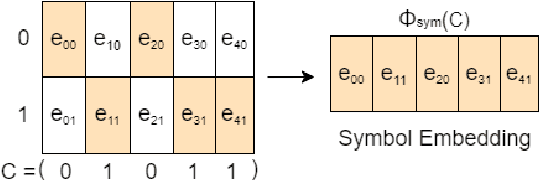
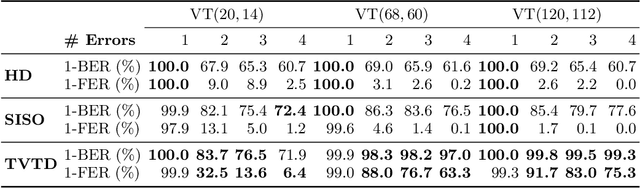

Abstract:In recent years, the rise of DNA data storage technology has brought significant attention to the challenge of correcting insertion, deletion, and substitution (IDS) errors. Among various coding methods for IDS correction, Varshamov-Tenengolts (VT) codes, primarily designed for single-error correction, have emerged as a central research focus. While existing decoding methods achieve high accuracy in correcting a single error, they often fail to correct multiple IDS errors. In this work, we observe that VT codes retain some capability for addressing multiple errors by introducing a transformer-based VT decoder (TVTD) along with symbol- and statistic-based codeword embedding. Experimental results demonstrate that the proposed TVTD achieves perfect correction of a single error. Furthermore, when decoding multiple errors across various codeword lengths, the bit error rate and frame error rate are significantly improved compared to existing hard decision and soft-in soft-out algorithms. Additionally, through model architecture optimization, the proposed method reduces time consumption by an order of magnitude compared to other soft decoders.
DoDo-Code: a Deep Levenshtein Distance Embedding-based Code for IDS Channel and DNA Storage
Dec 20, 2023Abstract:Recently, DNA storage has emerged as a promising data storage solution, offering significant advantages in storage density, maintenance cost efficiency, and parallel replication capability. Mathematically, the DNA storage pipeline can be viewed as an insertion, deletion, and substitution (IDS) channel. Because of the mathematical terra incognita of the Levenshtein distance, designing an IDS-correcting code is still a challenge. In this paper, we propose an innovative approach that utilizes deep Levenshtein distance embedding to bypass these mathematical challenges. By representing the Levenshtein distance between two sequences as a conventional distance between their corresponding embedding vectors, the inherent structural property of Levenshtein distance is revealed in the friendly embedding space. Leveraging this embedding space, we introduce the DoDo-Code, an IDS-correcting code that incorporates deep embedding of Levenshtein distance, deep embedding-based codeword search, and deep embedding-based segment correcting. To address the requirements of DNA storage, we also present a preliminary algorithm for long sequence decoding. As far as we know, the DoDo-Code is the first IDS-correcting code designed using plausible deep learning methodologies, potentially paving the way for a new direction in error-correcting code research. It is also the first IDS code that exhibits characteristics of being `optimal' in terms of redundancy, significantly outperforming the mainstream IDS-correcting codes of the Varshamov-Tenengolts code family in code rate.
Levenshtein Distance Embedding with Poisson Regression for DNA Storage
Dec 13, 2023
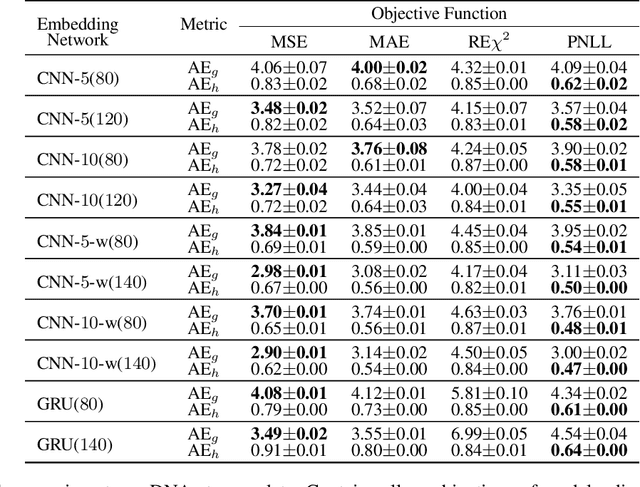
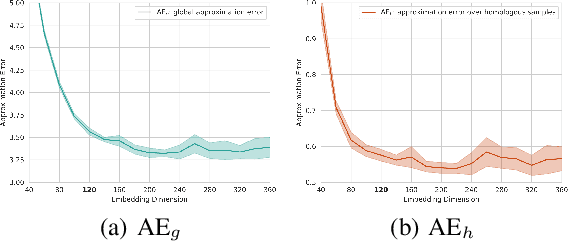
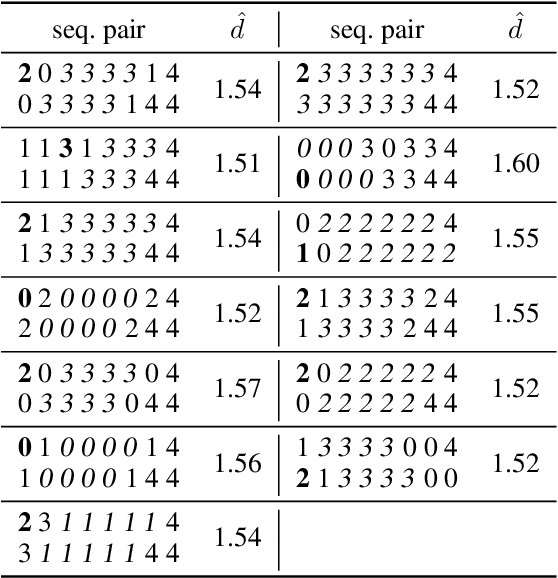
Abstract:Efficient computation or approximation of Levenshtein distance, a widely-used metric for evaluating sequence similarity, has attracted significant attention with the emergence of DNA storage and other biological applications. Sequence embedding, which maps Levenshtein distance to a conventional distance between embedding vectors, has emerged as a promising solution. In this paper, a novel neural network-based sequence embedding technique using Poisson regression is proposed. We first provide a theoretical analysis of the impact of embedding dimension on model performance and present a criterion for selecting an appropriate embedding dimension. Under this embedding dimension, the Poisson regression is introduced by assuming the Levenshtein distance between sequences of fixed length following a Poisson distribution, which naturally aligns with the definition of Levenshtein distance. Moreover, from the perspective of the distribution of embedding distances, Poisson regression approximates the negative log likelihood of the chi-squared distribution and offers advancements in removing the skewness. Through comprehensive experiments on real DNA storage data, we demonstrate the superior performance of the proposed method compared to state-of-the-art approaches.
Deep Squared Euclidean Approximation to the Levenshtein Distance for DNA Storage
Jul 11, 2022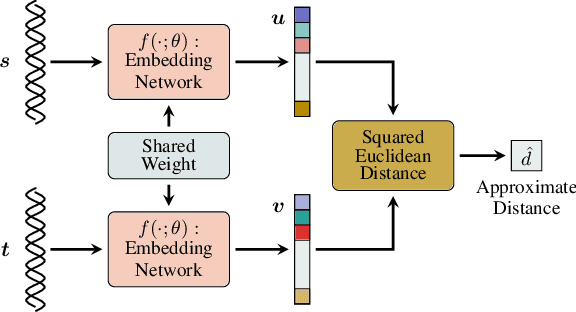

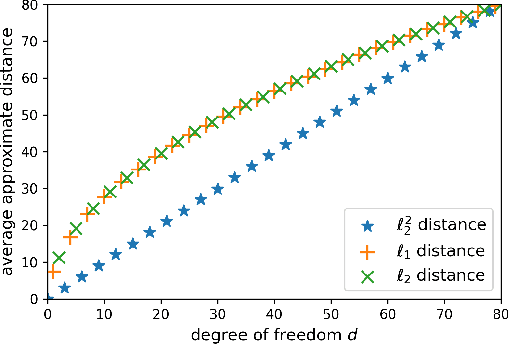
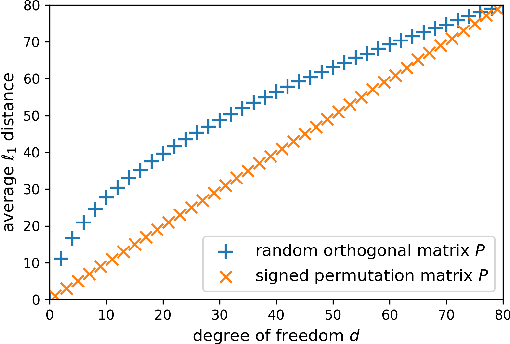
Abstract:Storing information in DNA molecules is of great interest because of its advantages in longevity, high storage density, and low maintenance cost. A key step in the DNA storage pipeline is to efficiently cluster the retrieved DNA sequences according to their similarities. Levenshtein distance is the most suitable metric on the similarity between two DNA sequences, but it is inferior in terms of computational complexity and less compatible with mature clustering algorithms. In this work, we propose a novel deep squared Euclidean embedding for DNA sequences using Siamese neural network, squared Euclidean embedding, and chi-squared regression. The Levenshtein distance is approximated by the squared Euclidean distance between the embedding vectors, which is fast calculated and clustering algorithm friendly. The proposed approach is analyzed theoretically and experimentally. The results show that the proposed embedding is efficient and robust.
Improving the Expressive Power of Graph Neural Network with Tinhofer Algorithm
Apr 05, 2021


Abstract:In recent years, Graph Neural Network (GNN) has bloomly progressed for its power in processing graph-based data. Most GNNs follow a message passing scheme, and their expressive power is mathematically limited by the discriminative ability of the Weisfeiler-Lehman (WL) test. Following Tinhofer's research on compact graphs, we propose a variation of the message passing scheme, called the Weisfeiler-Lehman-Tinhofer GNN (WLT-GNN), that theoretically breaks through the limitation of the WL test. In addition, we conduct comparative experiments and ablation studies on several well-known datasets. The results show that the proposed methods have comparable performances and better expressive power on these datasets.
Boosting Deep Hyperspectral Image Classification with Spectral Unmixing
Apr 03, 2020
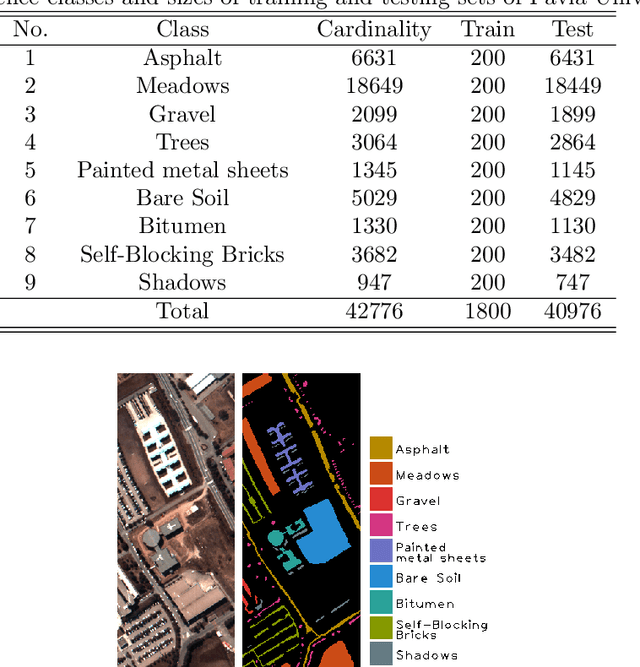
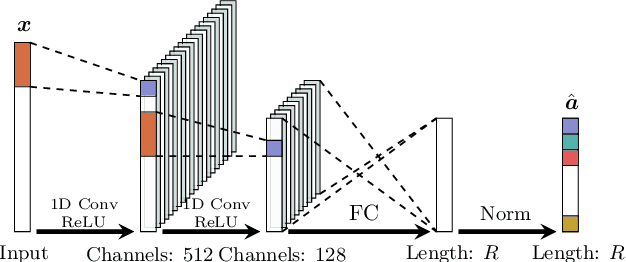
Abstract:Recent advances in neural networks have made great progress in addressing the hyperspectral image (HSI) classification problem. However, the overfitting effect, which is mainly caused by complicated model structure and small training set, remains a major concern when applying neural networks to HSIs analysis. Reducing the complexity of the neural networks could prevent overfitting to some extent, but it declines the networks' ability to extract more abstract features. Enlarging the training set is also difficult. To tackle the overfitting problem, we propose an abundance-based multi-HSI classification method. By applying an autoencoder-based spectral unmixing technique, different HSIs are firstly converted from the spectral domain to the abundance domain. After that, the abundance representations from multiple HSIs are collected to form an enlarged dataset. Lastly, a simple classifier is trained, which makes predictions over all the involved datasets. Taking advantage of the spectral unmixing, transforming the spectral features to the abundance features significantly simplifies the classification tasks. This enables the use of a simple network as the classifier, thus alleviating the overfitting effect. Moreover, as much dataset-specific information is eliminated by the spectral unmixing, a compatible classifier suitable for different HSIs is trained. A several times enlarged training set is constructed by assembling the abundances from different HSIs. The effectiveness of the proposed method is verified by the ablation study and the comparative experiments. On four datasets, the proposed method provides comparable results with two state-of-the-art methods, but using a much simpler model.
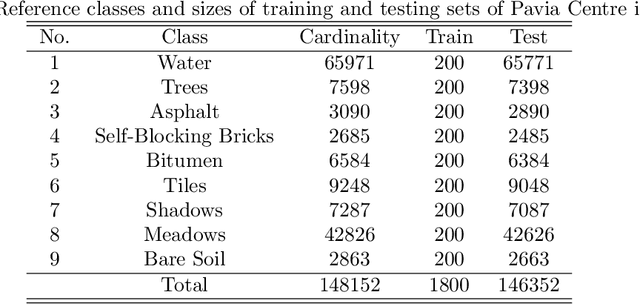
Hyperspectral Image Classification with Deep Metric Learning and Conditional Random Field
Mar 04, 2019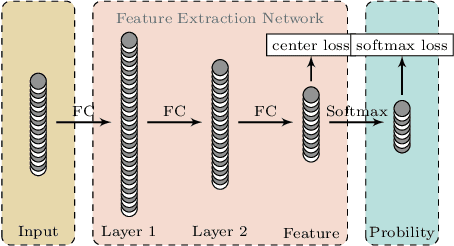
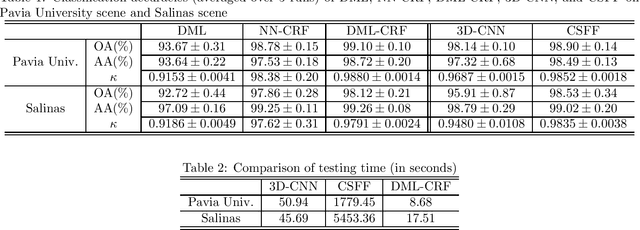
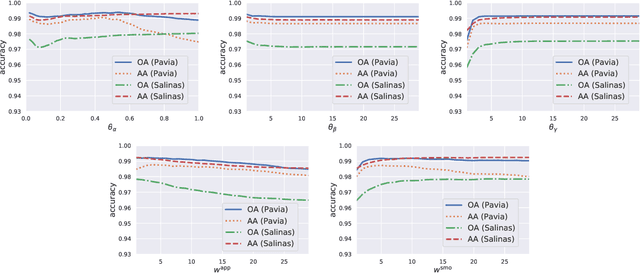

Abstract:To improve the classification performance in the context of hyperspectral image processing, many works have been developed based on two common strategies, namely the spatial-spectral information integration and the utilization of neural networks. However, both strategies typically require more training data than the classical algorithms, aggregating the shortage of labeled samples. In this paper, we propose a novel framework that organically combines an existing spectrum-based deep metric learning model and the conditional random field algorithm. The deep metric learning model is supervised by center loss, and is used to produce spectrum-based features that gather more tightly within classes in Euclidean space. The conditional random field with Gaussian edge potentials, which is firstly proposed for image segmentation problem, is utilized to jointly account for both the geometry distance of two pixels and the Euclidean distance between their corresponding features extracted by the deep metric learning model. The final predictions are given by the conditional random field. Generally, the proposed framework is trained by spectra pixels at the deep metric learning stage, and utilizes the half handcrafted spatial features at the conditional random field stage. This settlement alleviates the shortage of training data to some extent. Experiments on two real hyperspectral images demonstrate the advantages of the proposed method in terms of both classification accuracy and computation cost.
A CNN-based Spatial Feature Fusion Algorithm for Hyperspectral Imagery Classification
Aug 07, 2018
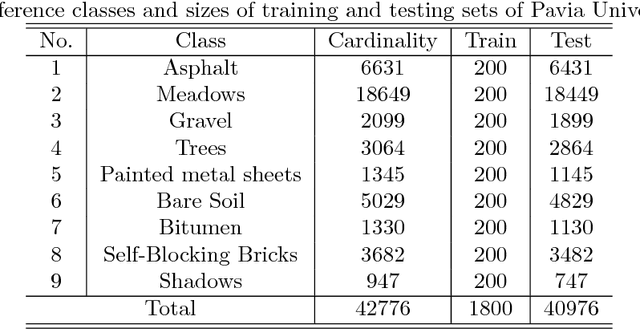
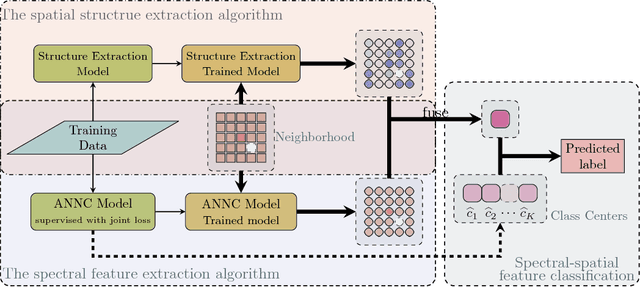
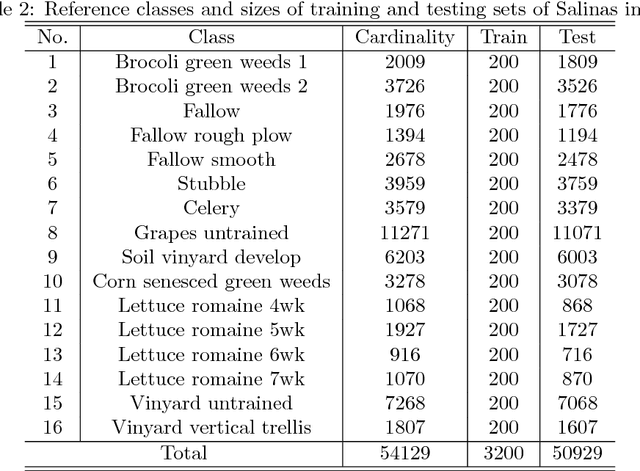
Abstract:The shortage of training samples remains one of the main obstacles in applying the artificial neural networks (ANN) to the hyperspectral images classification. To fuse the spatial and spectral information, pixel patches are often utilized to train a model, which may further aggregate this problem. In the existing works, an ANN model supervised by center-loss (ANNC) was introduced. Training merely with spectral information, the ANNC yields discriminative spectral features suitable for the subsequent classification tasks. In this paper, a CNN-based spatial feature fusion (CSFF) algorithm is proposed, which allows a smart fusion of the spatial information to the spectral features extracted by ANNC. As a critical part of CSFF, a CNN-based discriminant model is introduced to estimate whether two paring pixels belong to the same class. At the testing stage, by applying the discriminant model to the pixel-pairs generated by the test pixel and its neighbors, the local structure is estimated and represented as a customized convolutional kernel. The spectral-spatial feature is obtained by a convolutional operation between the estimated kernel and the corresponding spectral features within a neighborhood. At last, the label of the test pixel is predicted by classifying the resulting spectral-spatial feature. Without increasing the number of training samples or involving pixel patches at the training stage, the CSFF framework achieves the state-of-the-art by declining $20\%-50\%$ classification failures in experiments on three well-known hyperspectral images.
Spectral-Spatial Feature Extraction and Classification by ANN Supervised with Center Loss in Hyperspectral Imagery
Nov 20, 2017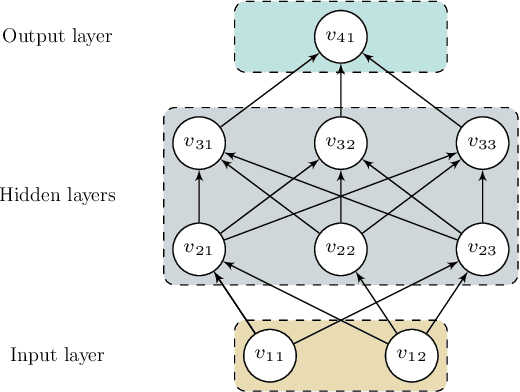
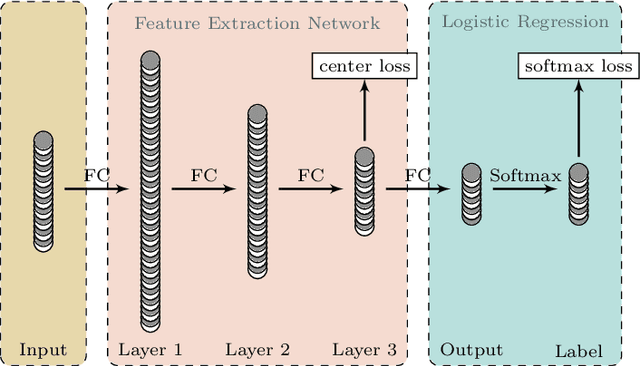
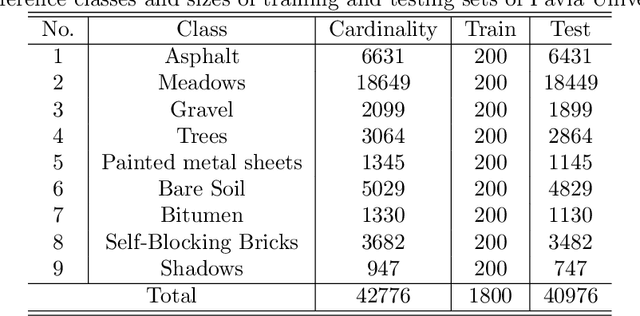
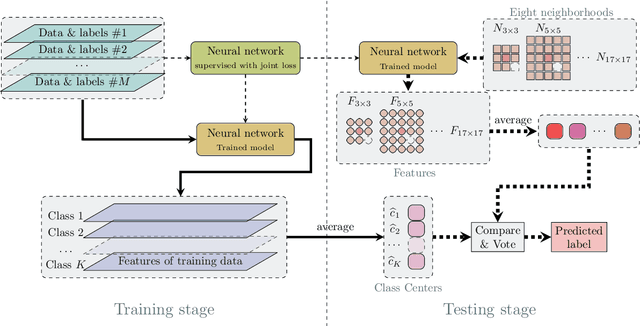
Abstract:In this paper, we propose a spectral-spatial feature extraction and classification framework based on artificial neuron network (ANN) in the context of hyperspectral imagery. With limited labeled samples, only spectral information is exploited for training and spatial context is integrated posteriorly at the testing stage. Taking advantage of recent advances in face recognition, a joint supervision symbol that combines softmax loss and center loss is adopted to train the proposed network, by which intra-class features are gathered while inter-class variations are enlarged. Based on the learned architecture, the extracted spectrum-based features are classified by a center classifier. Moreover, to fuse the spectral and spatial information, an adaptive spectral-spatial center classifier is developed, where multiscale neighborhoods are considered simultaneously, and the final label is determined using an adaptive voting strategy. Finally, experimental results on three well-known datasets validate the effectiveness of the proposed methods compared with the state-of-the-art approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge