DoDo-Code: a Deep Levenshtein Distance Embedding-based Code for IDS Channel and DNA Storage

Recently, DNA storage has emerged as a promising data storage solution, offering significant advantages in storage density, maintenance cost efficiency, and parallel replication capability. Mathematically, the DNA storage pipeline can be viewed as an insertion, deletion, and substitution (IDS) channel. Because of the mathematical terra incognita of the Levenshtein distance, designing an IDS-correcting code is still a challenge. In this paper, we propose an innovative approach that utilizes deep Levenshtein distance embedding to bypass these mathematical challenges. By representing the Levenshtein distance between two sequences as a conventional distance between their corresponding embedding vectors, the inherent structural property of Levenshtein distance is revealed in the friendly embedding space. Leveraging this embedding space, we introduce the DoDo-Code, an IDS-correcting code that incorporates deep embedding of Levenshtein distance, deep embedding-based codeword search, and deep embedding-based segment correcting. To address the requirements of DNA storage, we also present a preliminary algorithm for long sequence decoding. As far as we know, the DoDo-Code is the first IDS-correcting code designed using plausible deep learning methodologies, potentially paving the way for a new direction in error-correcting code research. It is also the first IDS code that exhibits characteristics of being `optimal' in terms of redundancy, significantly outperforming the mainstream IDS-correcting codes of the Varshamov-Tenengolts code family in code rate.

Levenshtein Distance Embedding with Poisson Regression for DNA Storage

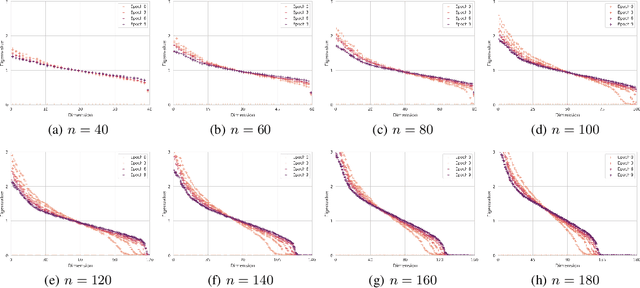
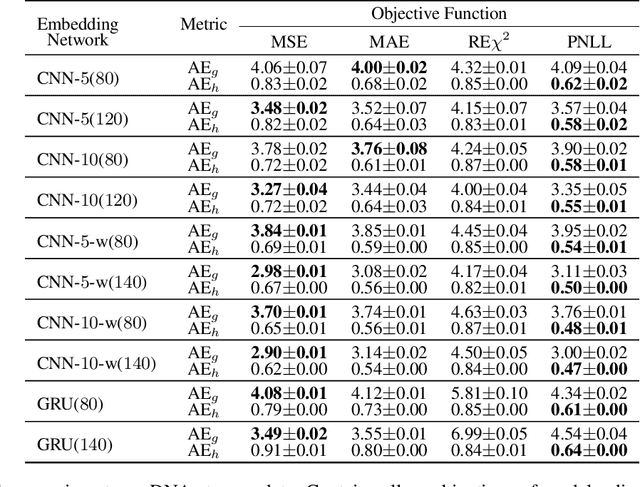
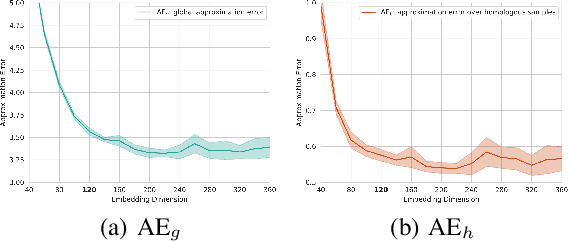
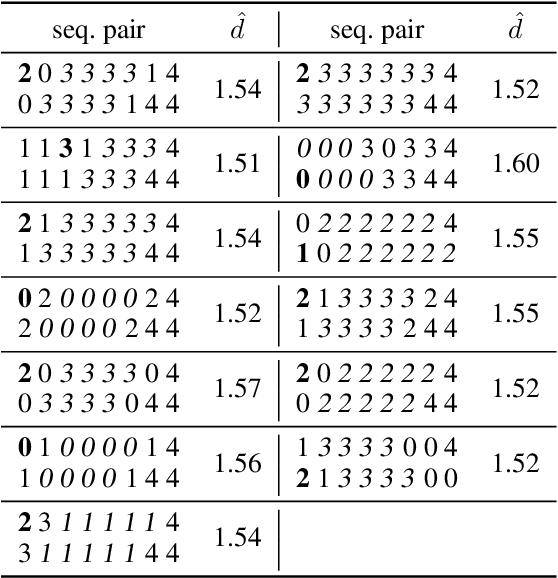
Efficient computation or approximation of Levenshtein distance, a widely-used metric for evaluating sequence similarity, has attracted significant attention with the emergence of DNA storage and other biological applications. Sequence embedding, which maps Levenshtein distance to a conventional distance between embedding vectors, has emerged as a promising solution. In this paper, a novel neural network-based sequence embedding technique using Poisson regression is proposed. We first provide a theoretical analysis of the impact of embedding dimension on model performance and present a criterion for selecting an appropriate embedding dimension. Under this embedding dimension, the Poisson regression is introduced by assuming the Levenshtein distance between sequences of fixed length following a Poisson distribution, which naturally aligns with the definition of Levenshtein distance. Moreover, from the perspective of the distribution of embedding distances, Poisson regression approximates the negative log likelihood of the chi-squared distribution and offers advancements in removing the skewness. Through comprehensive experiments on real DNA storage data, we demonstrate the superior performance of the proposed method compared to state-of-the-art approaches.