Deep Squared Euclidean Approximation to the Levenshtein Distance for DNA Storage

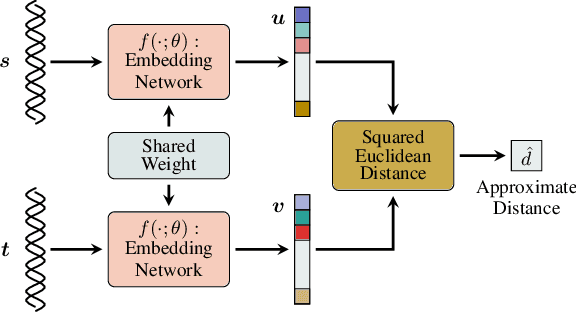
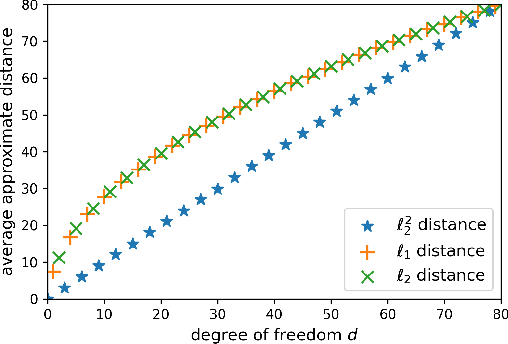
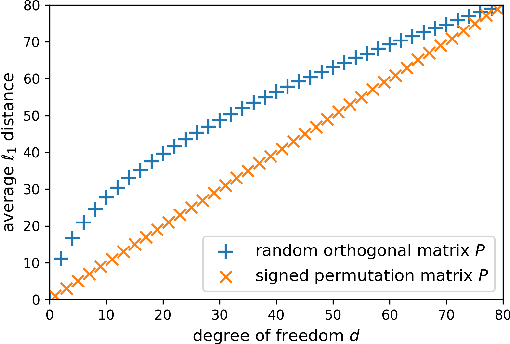
Storing information in DNA molecules is of great interest because of its advantages in longevity, high storage density, and low maintenance cost. A key step in the DNA storage pipeline is to efficiently cluster the retrieved DNA sequences according to their similarities. Levenshtein distance is the most suitable metric on the similarity between two DNA sequences, but it is inferior in terms of computational complexity and less compatible with mature clustering algorithms. In this work, we propose a novel deep squared Euclidean embedding for DNA sequences using Siamese neural network, squared Euclidean embedding, and chi-squared regression. The Levenshtein distance is approximated by the squared Euclidean distance between the embedding vectors, which is fast calculated and clustering algorithm friendly. The proposed approach is analyzed theoretically and experimentally. The results show that the proposed embedding is efficient and robust.

Improving the Expressive Power of Graph Neural Network with Tinhofer Algorithm

In recent years, Graph Neural Network (GNN) has bloomly progressed for its power in processing graph-based data. Most GNNs follow a message passing scheme, and their expressive power is mathematically limited by the discriminative ability of the Weisfeiler-Lehman (WL) test. Following Tinhofer's research on compact graphs, we propose a variation of the message passing scheme, called the Weisfeiler-Lehman-Tinhofer GNN (WLT-GNN), that theoretically breaks through the limitation of the WL test. In addition, we conduct comparative experiments and ablation studies on several well-known datasets. The results show that the proposed methods have comparable performances and better expressive power on these datasets.