Adrien Ali Taïga
Stop Regressing: Training Value Functions via Classification for Scalable Deep RL
Mar 06, 2024



Abstract:Value functions are a central component of deep reinforcement learning (RL). These functions, parameterized by neural networks, are trained using a mean squared error regression objective to match bootstrapped target values. However, scaling value-based RL methods that use regression to large networks, such as high-capacity Transformers, has proven challenging. This difficulty is in stark contrast to supervised learning: by leveraging a cross-entropy classification loss, supervised methods have scaled reliably to massive networks. Observing this discrepancy, in this paper, we investigate whether the scalability of deep RL can also be improved simply by using classification in place of regression for training value functions. We demonstrate that value functions trained with categorical cross-entropy significantly improves performance and scalability in a variety of domains. These include: single-task RL on Atari 2600 games with SoftMoEs, multi-task RL on Atari with large-scale ResNets, robotic manipulation with Q-transformers, playing Chess without search, and a language-agent Wordle task with high-capacity Transformers, achieving state-of-the-art results on these domains. Through careful analysis, we show that the benefits of categorical cross-entropy primarily stem from its ability to mitigate issues inherent to value-based RL, such as noisy targets and non-stationarity. Overall, we argue that a simple shift to training value functions with categorical cross-entropy can yield substantial improvements in the scalability of deep RL at little-to-no cost.
On Bonus-Based Exploration Methods in the Arcade Learning Environment
Sep 22, 2021



Abstract:Research on exploration in reinforcement learning, as applied to Atari 2600 game-playing, has emphasized tackling difficult exploration problems such as Montezuma's Revenge (Bellemare et al., 2016). Recently, bonus-based exploration methods, which explore by augmenting the environment reward, have reached above-human average performance on such domains. In this paper we reassess popular bonus-based exploration methods within a common evaluation framework. We combine Rainbow (Hessel et al., 2018) with different exploration bonuses and evaluate its performance on Montezuma's Revenge, Bellemare et al.'s set of hard of exploration games with sparse rewards, and the whole Atari 2600 suite. We find that while exploration bonuses lead to higher score on Montezuma's Revenge they do not provide meaningful gains over the simpler $\epsilon$-greedy scheme. In fact, we find that methods that perform best on that game often underperform $\epsilon$-greedy on easy exploration Atari 2600 games. We find that our conclusions remain valid even when hyperparameters are tuned for these easy-exploration games. Finally, we find that none of the methods surveyed benefit from additional training samples (1 billion frames, versus Rainbow's 200 million) on Bellemare et al.'s hard exploration games. Our results suggest that recent gains in Montezuma's Revenge may be better attributed to architecture change, rather than better exploration schemes; and that the real pace of progress in exploration research for Atari 2600 games may have been obfuscated by good results on a single domain.
* Full version of arXiv:1908.02388
Benchmarking Bonus-Based Exploration Methods on the Arcade Learning Environment
Aug 06, 2019



Abstract:This paper provides an empirical evaluation of recently developed exploration algorithms within the Arcade Learning Environment (ALE). We study the use of different reward bonuses that incentives exploration in reinforcement learning. We do so by fixing the learning algorithm used and focusing only on the impact of the different exploration bonuses in the agent's performance. We use Rainbow, the state-of-the-art algorithm for value-based agents, and focus on some of the bonuses proposed in the last few years. We consider the impact these algorithms have on performance within the popular game Montezuma's Revenge which has gathered a lot of interest from the exploration community, across the the set of seven games identified by Bellemare et al. (2016) as challenging for exploration, and easier games where exploration is not an issue. We find that, in our setting, recently developed bonuses do not provide significantly improved performance on Montezuma's Revenge or hard exploration games. We also find that existing bonus-based methods may negatively impact performance on games in which exploration is not an issue and may even perform worse than $\epsilon$-greedy exploration.
The Value Function Polytope in Reinforcement Learning
Feb 15, 2019



Abstract:We establish geometric and topological properties of the space of value functions in finite state-action Markov decision processes. Our main contribution is the characterization of the nature of its shape: a general polytope (Aigner et al., 2010). To demonstrate this result, we exhibit several properties of the structural relationship between policies and value functions including the line theorem, which shows that the value functions of policies constrained on all but one state describe a line segment. Finally, we use this novel perspective to introduce visualizations to enhance the understanding of the dynamics of reinforcement learning algorithms.
Approximate Exploration through State Abstraction
Aug 29, 2018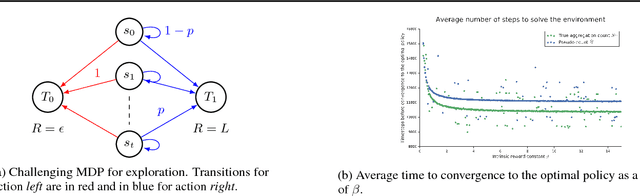

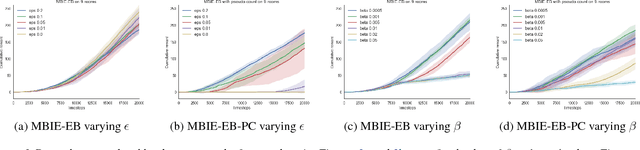
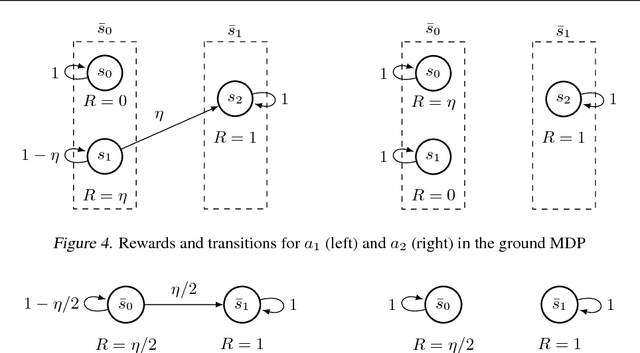
Abstract:Although exploration in reinforcement learning is well understood from a theoretical point of view, provably correct methods remain impractical. In this paper we study the interplay between exploration and approximation, what we call \emph{approximate exploration}. We first provide results when the approximation is explicit, quantifying the performance of an exploration algorithm, MBIE-EB \citep{strehl2008analysis}, when combined with state aggregation. In particular, we show that this allows the agent to trade off between learning speed and quality of the policy learned. We then turn to a successful exploration scheme in practical, pseudo-count based exploration bonuses \citep{bellemare2016unifying}. We show that choosing a density model implicitly defines an abstraction and that the pseudo-count bonus incentivizes the agent to explore using this abstraction. We find, however, that implicit exploration may result in a mismatch between the approximated value function and exploration bonus, leading to either under- or over-exploration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge