Approximate Exploration through State Abstraction

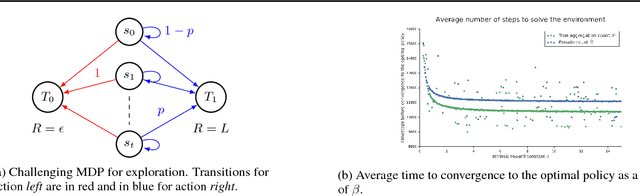
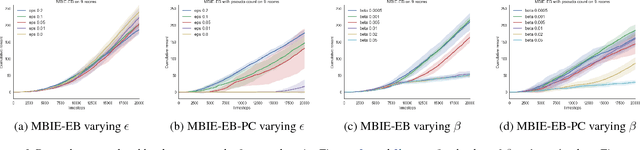
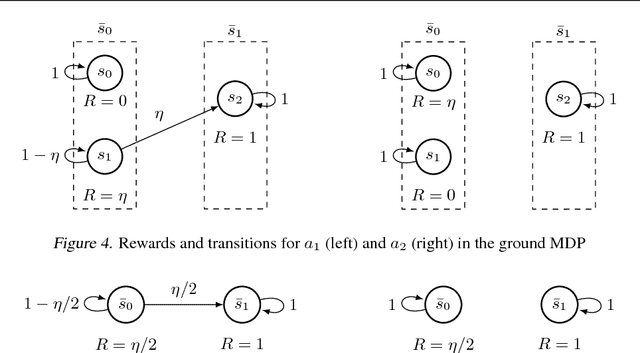
Although exploration in reinforcement learning is well understood from a theoretical point of view, provably correct methods remain impractical. In this paper we study the interplay between exploration and approximation, what we call \emph{approximate exploration}. We first provide results when the approximation is explicit, quantifying the performance of an exploration algorithm, MBIE-EB \citep{strehl2008analysis}, when combined with state aggregation. In particular, we show that this allows the agent to trade off between learning speed and quality of the policy learned. We then turn to a successful exploration scheme in practical, pseudo-count based exploration bonuses \citep{bellemare2016unifying}. We show that choosing a density model implicitly defines an abstraction and that the pseudo-count bonus incentivizes the agent to explore using this abstraction. We find, however, that implicit exploration may result in a mismatch between the approximated value function and exploration bonus, leading to either under- or over-exploration.