See What You Need: Query-Aware Visual Intelligence through Reasoning-Perception Loops

Human video comprehension demonstrates dynamic coordination between reasoning and visual attention, adaptively focusing on query-relevant details. However, current long-form video question answering systems employ rigid pipelines that decouple reasoning from perception, leading to either information loss through premature visual abstraction or computational inefficiency through exhaustive processing. The core limitation lies in the inability to adapt visual extraction to specific reasoning requirements, different queries demand fundamentally different visual evidence from the same video content. In this work, we present CAVIA, a training-free framework that revolutionizes video understanding through reasoning, perception coordination. Unlike conventional approaches where visual processing operates independently of reasoning, CAVIA creates a closed-loop system where reasoning continuously guides visual extraction based on identified information gaps. CAVIA introduces three innovations: (1) hierarchical reasoning, guided localization to precise frames; (2) cross-modal semantic bridging for targeted extraction; (3) confidence-driven iterative synthesis. CAVIA achieves state-of-the-art performance on challenging benchmarks: EgoSchema (65.7%, +5.3%), NExT-QA (76.1%, +2.6%), and IntentQA (73.8%, +6.9%), demonstrating that dynamic reasoning-perception coordination provides a scalable paradigm for video understanding.

Is Optimal Transport Necessary for Inverse Reinforcement Learning?

Inverse Reinforcement Learning (IRL) aims to recover a reward function from expert demonstrations. Recently, Optimal Transport (OT) methods have been successfully deployed to align trajectories and infer rewards. While OT-based methods have shown strong empirical results, they introduce algorithmic complexity, hyperparameter sensitivity, and require solving the OT optimization problems. In this work, we challenge the necessity of OT in IRL by proposing two simple, heuristic alternatives: (1) Minimum-Distance Reward, which assigns rewards based on the nearest expert state regardless of temporal order; and (2) Segment-Matching Reward, which incorporates lightweight temporal alignment by matching agent states to corresponding segments in the expert trajectory. These methods avoid optimization, exhibit linear-time complexity, and are easy to implement. Through extensive evaluations across 32 online and offline benchmarks with three reinforcement learning algorithms, we show that our simple rewards match or outperform recent OT-based approaches. Our findings suggest that the core benefits of OT may arise from basic proximity alignment rather than its optimal coupling formulation, advocating for reevaluation of complexity in future IRL design.

The Prevalence of Neural Collapse in Neural Multivariate Regression

Recently it has been observed that neural networks exhibit Neural Collapse (NC) during the final stage of training for the classification problem. We empirically show that multivariate regression, as employed in imitation learning and other applications, exhibits Neural Regression Collapse (NRC), a new form of neural collapse: (NRC1) The last-layer feature vectors collapse to the subspace spanned by the $n$ principal components of the feature vectors, where $n$ is the dimension of the targets (for univariate regression, $n=1$); (NRC2) The last-layer feature vectors also collapse to the subspace spanned by the last-layer weight vectors; (NRC3) The Gram matrix for the weight vectors converges to a specific functional form that depends on the covariance matrix of the targets. After empirically establishing the prevalence of (NRC1)-(NRC3) for a variety of datasets and network architectures, we provide an explanation of these phenomena by modeling the regression task in the context of the Unconstrained Feature Model (UFM), in which the last layer feature vectors are treated as free variables when minimizing the loss function. We show that when the regularization parameters in the UFM model are strictly positive, then (NRC1)-(NRC3) also emerge as solutions in the UFM optimization problem. We also show that if the regularization parameters are equal to zero, then there is no collapse. To our knowledge, this is the first empirical and theoretical study of neural collapse in the context of regression. This extension is significant not only because it broadens the applicability of neural collapse to a new category of problems but also because it suggests that the phenomena of neural collapse could be a universal behavior in deep learning.

EffiQA: Efficient Question-Answering with Strategic Multi-Model Collaboration on Knowledge Graphs

While large language models (LLMs) have shown remarkable capabilities in natural language processing, they struggle with complex, multi-step reasoning tasks involving knowledge graphs (KGs). Existing approaches that integrate LLMs and KGs either underutilize the reasoning abilities of LLMs or suffer from prohibitive computational costs due to tight coupling. To address these limitations, we propose a novel collaborative framework named EffiQA that can strike a balance between performance and efficiency via an iterative paradigm. EffiQA consists of three stages: global planning, efficient KG exploration, and self-reflection. Specifically, EffiQA leverages the commonsense capability of LLMs to explore potential reasoning pathways through global planning. Then, it offloads semantic pruning to a small plug-in model for efficient KG exploration. Finally, the exploration results are fed to LLMs for self-reflection to further improve the global planning and efficient KG exploration. Empirical evidence on multiple KBQA benchmarks shows EffiQA's effectiveness, achieving an optimal balance between reasoning accuracy and computational costs. We hope the proposed new framework will pave the way for efficient, knowledge-intensive querying by redefining the integration of LLMs and KGs, fostering future research on knowledge-based question answering.

Cross Entropy versus Label Smoothing: A Neural Collapse Perspective

Label smoothing loss is a widely adopted technique to mitigate overfitting in deep neural networks. This paper studies label smoothing from the perspective of Neural Collapse (NC), a powerful empirical and theoretical framework which characterizes model behavior during the terminal phase of training. We first show empirically that models trained with label smoothing converge faster to neural collapse solutions and attain a stronger level of neural collapse. Additionally, we show that at the same level of NC1, models under label smoothing loss exhibit intensified NC2. These findings provide valuable insights into the performance benefits and enhanced model calibration under label smoothing loss. We then leverage the unconstrained feature model to derive closed-form solutions for the global minimizers for both loss functions and further demonstrate that models under label smoothing have a lower conditioning number and, therefore, theoretically converge faster. Our study, combining empirical evidence and theoretical results, not only provides nuanced insights into the differences between label smoothing and cross-entropy losses, but also serves as an example of how the powerful neural collapse framework can be used to improve our understanding of DNNs.

Pre-training with Synthetic Data Helps Offline Reinforcement Learning

Recently, it has been shown that for offline deep reinforcement learning (DRL), pre-training Decision Transformer with a large language corpus can improve downstream performance (Reid et al., 2022). A natural question to ask is whether this performance gain can only be achieved with language pre-training, or can be achieved with simpler pre-training schemes which do not involve language. In this paper, we first show that language is not essential for improved performance, and indeed pre-training with synthetic IID data for a small number of updates can match the performance gains from pre-training with a large language corpus; moreover, pre-training with data generated by a one-step Markov chain can further improve the performance. Inspired by these experimental results, we then consider pre-training Conservative Q-Learning (CQL), a popular offline DRL algorithm, which is Q-learning-based and typically employs a Multi-Layer Perceptron (MLP) backbone. Surprisingly, pre-training with simple synthetic data for a small number of updates can also improve CQL, providing consistent performance improvement on D4RL Gym locomotion datasets. The results of this paper not only illustrate the importance of pre-training for offline DRL but also show that the pre-training data can be synthetic and generated with remarkably simple mechanisms.

On the Convergence of Monte Carlo UCB for Random-Length Episodic MDPs

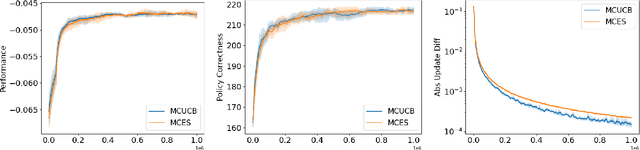
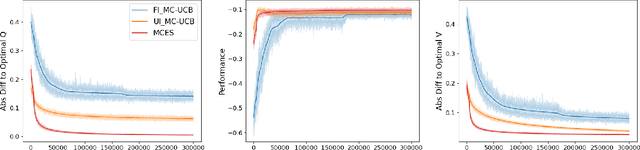
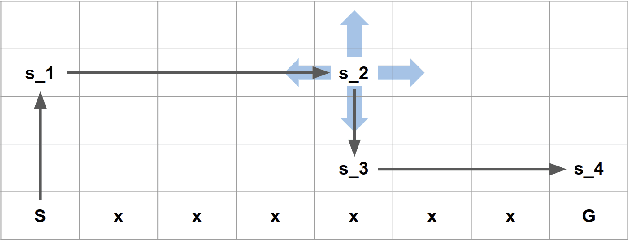
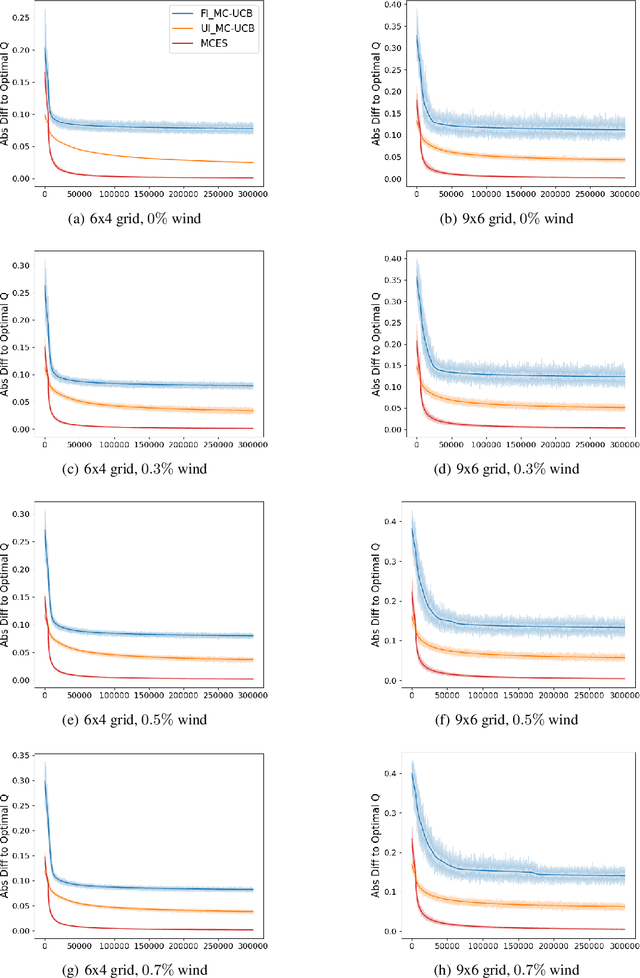
In reinforcement learning, Monte Carlo algorithms update the Q function by averaging the episodic returns. In the Monte Carlo UCB (MC-UCB) algorithm, the action taken in each state is the action that maximizes the Q function plus a UCB exploration term, which biases the choice of actions to those that have been chosen less frequently. Although there has been significant work on establishing regret bounds for MC-UCB, most of that work has been focused on finite-horizon versions of the problem, for which each episode terminates after a constant number of steps. For such finite-horizon problems, the optimal policy depends both on the current state and the time within the episode. However, for many natural episodic problems, such as games like Go and Chess and robotic tasks, the episode is of random length and the optimal policy is stationary. For such environments, it is an open question whether the Q-function in MC-UCB will converge to the optimal Q function; we conjecture that, unlike Q-learning, it does not converge for all MDPs. We nevertheless show that for a large class of MDPs, which includes stochastic MDPs such as blackjack and deterministic MDPs such as Go, the Q-function in MC-UCB converges almost surely to the optimal Q function. An immediate corollary of this result is that it also converges almost surely for all finite-horizon MDPs. We also provide numerical experiments, providing further insights into MC-UCB.