Analytic Personalized Federated Meta-Learning

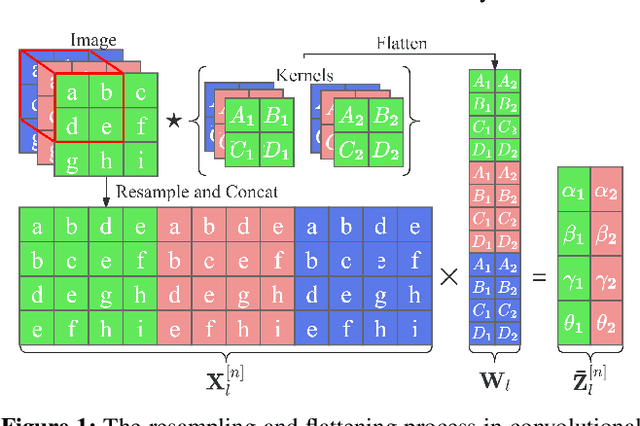
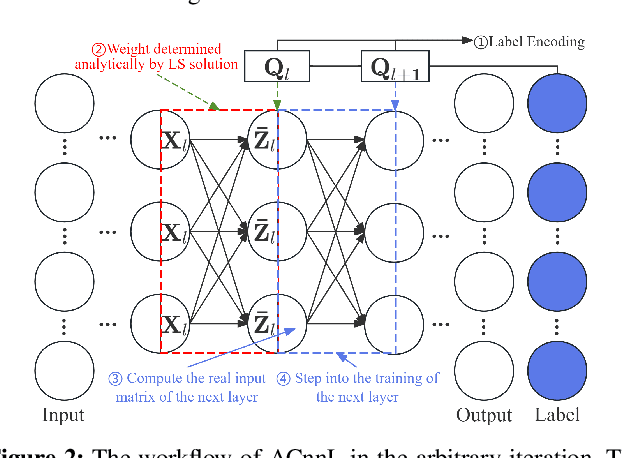
Analytic federated learning (AFL) which updates model weights only once by using closed-form least-square (LS) solutions can reduce abundant training time in gradient-free federated learning (FL). The current AFL framework cannot support deep neural network (DNN) training, which hinders its implementation on complex machine learning tasks. Meanwhile, it overlooks the heterogeneous data distribution problem that restricts the single global model from performing well on each client's task. To overcome the first challenge, we propose an AFL framework, namely FedACnnL, in which we resort to a novel local analytic learning method (ACnnL) and model the training of each layer as a distributed LS problem. For the second challenge, we propose an analytic personalized federated meta-learning framework, namely pFedACnnL, which is inherited from FedACnnL. In pFedACnnL, clients with similar data distribution share a common robust global model for fast adapting it to local tasks in an analytic manner. FedACnnL is theoretically proven to require significantly shorter training time than the conventional zeroth-order (i.e. gradient-free) FL frameworks on DNN training while the reduction ratio is $98\%$ in the experiment. Meanwhile, pFedACnnL achieves state-of-the-art (SOTA) model performance in most cases of convex and non-convex settings, compared with the previous SOTA frameworks.

Compressing Model with Few Class-Imbalance Samples: An Out-of-Distribution Expedition

In recent years, as a compromise between privacy and performance, few-sample model compression has been widely adopted to deal with limited data resulting from privacy and security concerns. However, when the number of available samples is extremely limited, class imbalance becomes a common and tricky problem. Achieving an equal number of samples across all classes is often costly and impractical in real-world applications, and previous studies on few-sample model compression have mostly ignored this significant issue. Our experiments comprehensively demonstrate that class imbalance negatively affects the overall performance of few-sample model compression methods. To address this problem, we propose a novel and adaptive framework named OOD-Enhanced Few-Sample Model Compression (OE-FSMC). This framework integrates easily accessible out-of-distribution (OOD) data into both the compression and fine-tuning processes, effectively rebalancing the training distribution. We also incorporate a joint distillation loss and a regularization term to reduce the risk of the model overfitting to the OOD data. Extensive experiments on multiple benchmark datasets show that our framework can be seamlessly incorporated into existing few-sample model compression methods, effectively mitigating the accuracy degradation caused by class imbalance.

Mask-Encoded Sparsification: Mitigating Biased Gradients in Communication-Efficient Split Learning

This paper introduces a novel framework designed to achieve a high compression ratio in Split Learning (SL) scenarios where resource-constrained devices are involved in large-scale model training. Our investigations demonstrate that compressing feature maps within SL leads to biased gradients that can negatively impact the convergence rates and diminish the generalization capabilities of the resulting models. Our theoretical analysis provides insights into how compression errors critically hinder SL performance, which previous methodologies underestimate. To address these challenges, we employ a narrow bit-width encoded mask to compensate for the sparsification error without increasing the order of time complexity. Supported by rigorous theoretical analysis, our framework significantly reduces compression errors and accelerates the convergence. Extensive experiments also verify that our method outperforms existing solutions regarding training efficiency and communication complexity.

Accelerating Federated Learning via Sampling Anchor Clients with Large Batches

Using large batches in recent federated learning studies has improved convergence rates, but it requires additional computation overhead compared to using small batches. To overcome this limitation, we propose a unified framework FedAMD, which disjoints the participants into anchor and miner groups based on time-varying probabilities. Each client in the anchor group computes the gradient using a large batch, which is regarded as its bullseye. Clients in the miner group perform multiple local updates using serial mini-batches, and each local update is also indirectly regulated by the global target derived from the average of clients' bullseyes. As a result, the miner group follows a near-optimal update towards the global minimizer, adapted to update the global model. Measured by $\epsilon$-approximation, FedAMD achieves a convergence rate of $O(1/\epsilon)$ under non-convex objectives by sampling an anchor with a constant probability. The theoretical result considerably surpasses the state-of-the-art algorithm BVR-L-SGD at $O(1/\epsilon^{3/2})$, while FedAMD reduces at least $O(1/\epsilon)$ communication overhead. Empirical studies on real-world datasets validate the effectiveness of FedAMD and demonstrate the superiority of our proposed algorithm.

Sign Bit is Enough: A Learning Synchronization Framework for Multi-hop All-reduce with Ultimate Compression

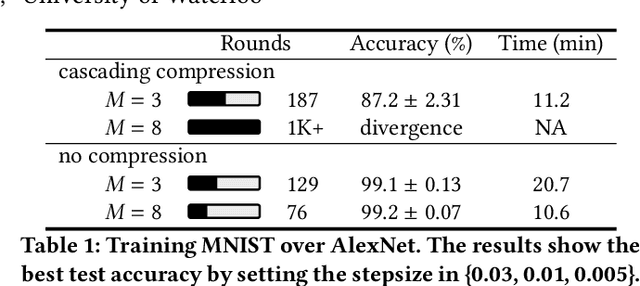
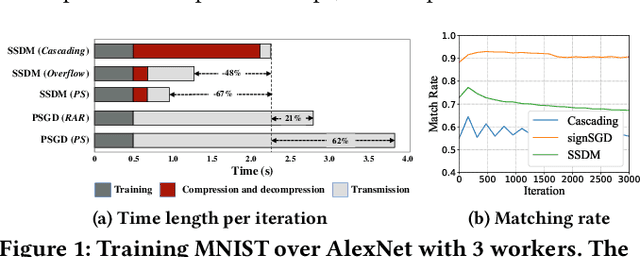
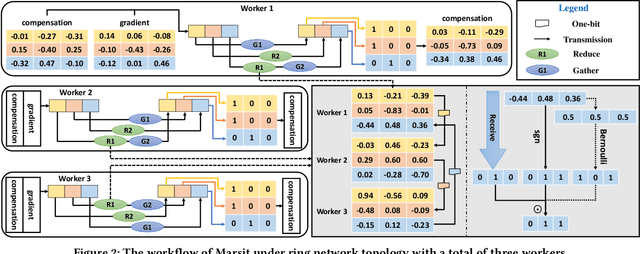
Traditional one-bit compressed stochastic gradient descent can not be directly employed in multi-hop all-reduce, a widely adopted distributed training paradigm in network-intensive high-performance computing systems such as public clouds. According to our theoretical findings, due to the cascading compression, the training process has considerable deterioration on the convergence performance. To overcome this limitation, we implement a sign-bit compression-based learning synchronization framework, Marsit. It prevents cascading compression via an elaborate bit-wise operation for unbiased sign aggregation and its specific global compensation mechanism for mitigating compression deviation. The proposed framework retains the same theoretical convergence rate as non-compression mechanisms. Experimental results demonstrate that Marsit reduces up to 35% training time while preserving the same accuracy as training without compression.

From Deterioration to Acceleration: A Calibration Approach to Rehabilitating Step Asynchronism in Federated Optimization

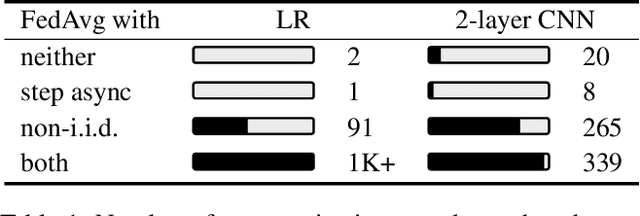
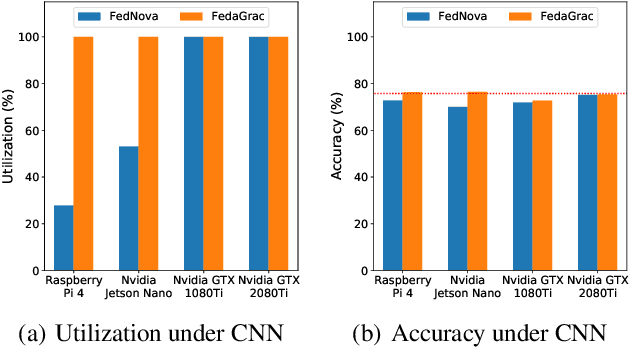
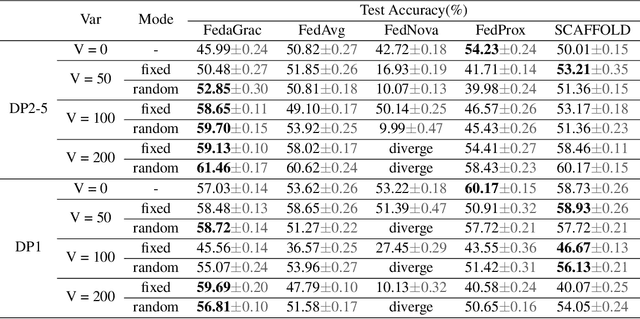
In the setting of federated optimization, where a global model is aggregated periodically, step asynchronism occurs when participants conduct model training with fully utilizing their computational resources. It is well acknowledged that step asynchronism leads to objective inconsistency under non-i.i.d. data, which degrades the model accuracy. To address this issue, we propose a new algorithm \texttt{FedaGrac}, which calibrates the local direction to a predictive global orientation. Taking the advantage of estimated orientation, we guarantee that the aggregated model does not excessively deviate from the expected orientation while fully utilizing the local updates of faster nodes. We theoretically prove that \texttt{FedaGrac} holds an improved order of convergence rate than the state-of-the-art approaches and eliminates the negative effect of step asynchronism. Empirical results show that our algorithm accelerates the training and enhances the final accuracy.

Intermittent Pulling with Local Compensation for Communication-Efficient Federated Learning

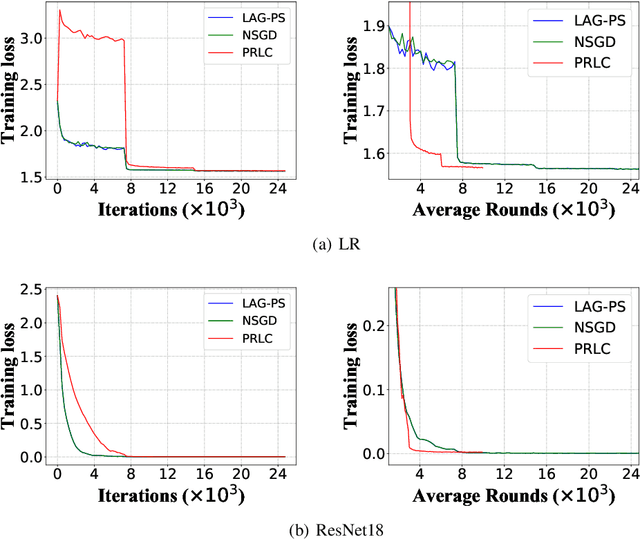
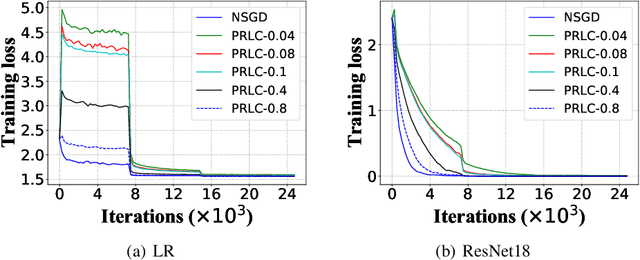
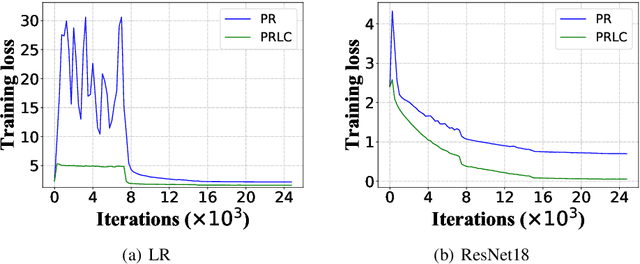
Federated Learning is a powerful machine learning paradigm to cooperatively train a global model with highly distributed data. A major bottleneck on the performance of distributed Stochastic Gradient Descent (SGD) algorithm for large-scale Federated Learning is the communication overhead on pushing local gradients and pulling global model. In this paper, to reduce the communication complexity of Federated Learning, a novel approach named Pulling Reduction with Local Compensation (PRLC) is proposed. Specifically, each training node intermittently pulls the global model from the server in SGD iterations, resulting in that it is sometimes unsynchronized with the server. In such a case, it will use its local update to compensate the gap between the local model and the global model. Our rigorous theoretical analysis of PRLC achieves two important findings. First, we prove that the convergence rate of PRLC preserves the same order as the classical synchronous SGD for both strongly-convex and non-convex cases with good scalability due to the linear speedup with respect to the number of training nodes. Second, we show that PRLC admits lower pulling frequency than the existing pulling reduction method without local compensation. We also conduct extensive experiments on various machine learning models to validate our theoretical results. Experimental results show that our approach achieves a significant pulling reduction over the state-of-the-art methods, e.g., PRLC requiring only half of the pulling operations of LAG.