Accelerating Deep Neural Network Training via Distributed Hybrid Order Optimization

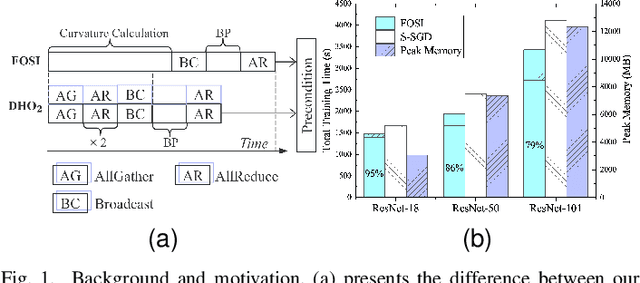
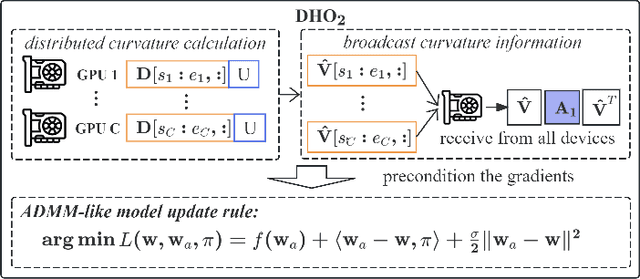
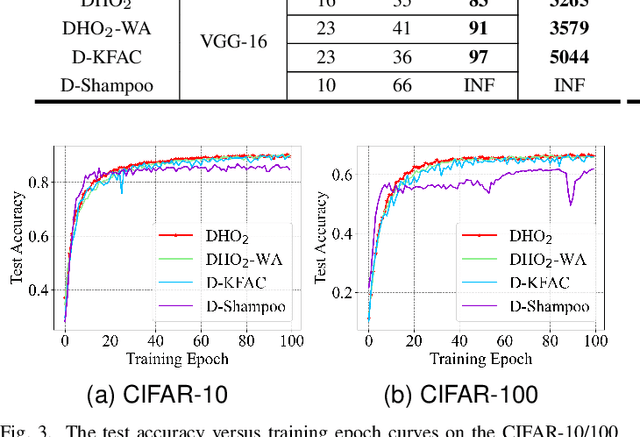
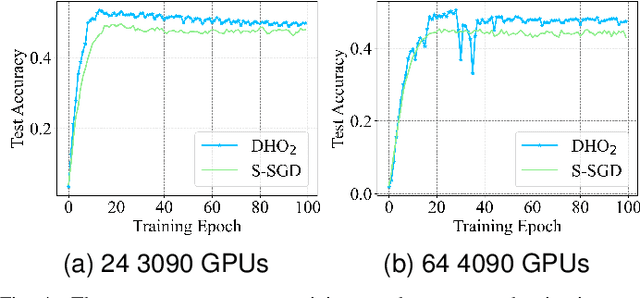
Scaling deep neural network (DNN) training to more devices can reduce time-to-solution. However, it is impractical for users with limited computing resources. FOSI, as a hybrid order optimizer, converges faster than conventional optimizers by taking advantage of both gradient information and curvature information when updating the DNN model. Therefore, it provides a new chance for accelerating DNN training in the resource-constrained setting. In this paper, we explore its distributed design, namely DHO$_2$, including distributed calculation of curvature information and model update with partial curvature information to accelerate DNN training with a low memory burden. To further reduce the training time, we design a novel strategy to parallelize the calculation of curvature information and the model update on different devices. Experimentally, our distributed design can achieve an approximate linear reduction of memory burden on each device with the increase of the device number. Meanwhile, it achieves $1.4\times\sim2.1\times$ speedup in the total training time compared with other distributed designs based on conventional first- and second-order optimizers.

Analytic Personalized Federated Meta-Learning

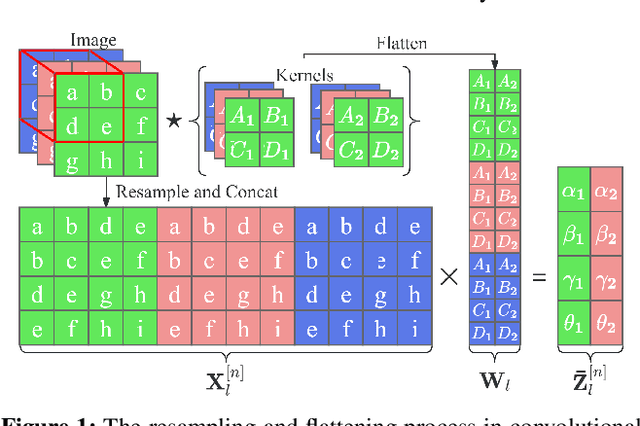
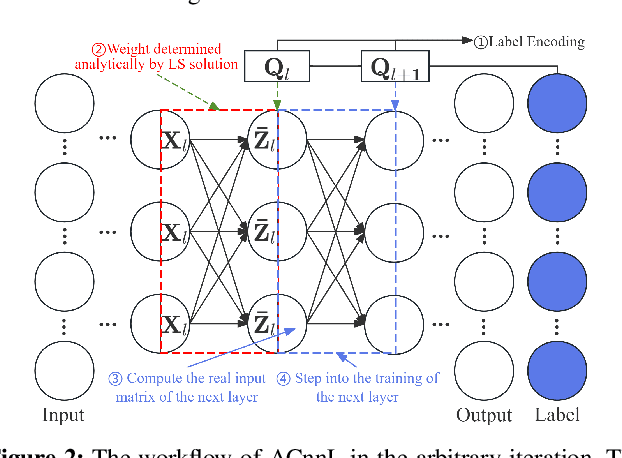
Analytic federated learning (AFL) which updates model weights only once by using closed-form least-square (LS) solutions can reduce abundant training time in gradient-free federated learning (FL). The current AFL framework cannot support deep neural network (DNN) training, which hinders its implementation on complex machine learning tasks. Meanwhile, it overlooks the heterogeneous data distribution problem that restricts the single global model from performing well on each client's task. To overcome the first challenge, we propose an AFL framework, namely FedACnnL, in which we resort to a novel local analytic learning method (ACnnL) and model the training of each layer as a distributed LS problem. For the second challenge, we propose an analytic personalized federated meta-learning framework, namely pFedACnnL, which is inherited from FedACnnL. In pFedACnnL, clients with similar data distribution share a common robust global model for fast adapting it to local tasks in an analytic manner. FedACnnL is theoretically proven to require significantly shorter training time than the conventional zeroth-order (i.e. gradient-free) FL frameworks on DNN training while the reduction ratio is $98\%$ in the experiment. Meanwhile, pFedACnnL achieves state-of-the-art (SOTA) model performance in most cases of convex and non-convex settings, compared with the previous SOTA frameworks.