Compressing Model with Few Class-Imbalance Samples: An Out-of-Distribution Expedition

In recent years, as a compromise between privacy and performance, few-sample model compression has been widely adopted to deal with limited data resulting from privacy and security concerns. However, when the number of available samples is extremely limited, class imbalance becomes a common and tricky problem. Achieving an equal number of samples across all classes is often costly and impractical in real-world applications, and previous studies on few-sample model compression have mostly ignored this significant issue. Our experiments comprehensively demonstrate that class imbalance negatively affects the overall performance of few-sample model compression methods. To address this problem, we propose a novel and adaptive framework named OOD-Enhanced Few-Sample Model Compression (OE-FSMC). This framework integrates easily accessible out-of-distribution (OOD) data into both the compression and fine-tuning processes, effectively rebalancing the training distribution. We also incorporate a joint distillation loss and a regularization term to reduce the risk of the model overfitting to the OOD data. Extensive experiments on multiple benchmark datasets show that our framework can be seamlessly incorporated into existing few-sample model compression methods, effectively mitigating the accuracy degradation caused by class imbalance.

Mask-Encoded Sparsification: Mitigating Biased Gradients in Communication-Efficient Split Learning

This paper introduces a novel framework designed to achieve a high compression ratio in Split Learning (SL) scenarios where resource-constrained devices are involved in large-scale model training. Our investigations demonstrate that compressing feature maps within SL leads to biased gradients that can negatively impact the convergence rates and diminish the generalization capabilities of the resulting models. Our theoretical analysis provides insights into how compression errors critically hinder SL performance, which previous methodologies underestimate. To address these challenges, we employ a narrow bit-width encoded mask to compensate for the sparsification error without increasing the order of time complexity. Supported by rigorous theoretical analysis, our framework significantly reduces compression errors and accelerates the convergence. Extensive experiments also verify that our method outperforms existing solutions regarding training efficiency and communication complexity.

The Role of Depth, Width, and Tree Size in Expressiveness of Deep Forest

Random forests are classical ensemble algorithms that construct multiple randomized decision trees and aggregate their predictions using naive averaging. \citet{zhou2019deep} further propose a deep forest algorithm with multi-layer forests, which outperforms random forests in various tasks. The performance of deep forests is related to three hyperparameters in practice: depth, width, and tree size, but little has been known about its theoretical explanation. This work provides the first upper and lower bounds on the approximation complexity of deep forests concerning the three hyperparameters. Our results confirm the distinctive role of depth, which can exponentially enhance the expressiveness of deep forests compared with width and tree size. Experiments confirm the theoretical findings.

Intermittent Pulling with Local Compensation for Communication-Efficient Federated Learning

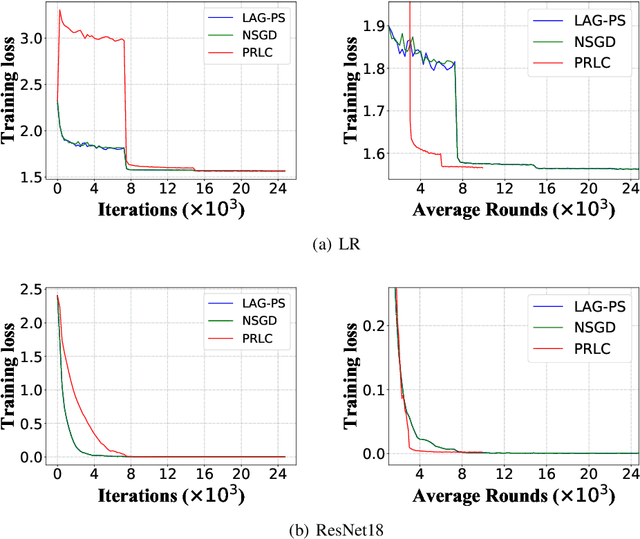
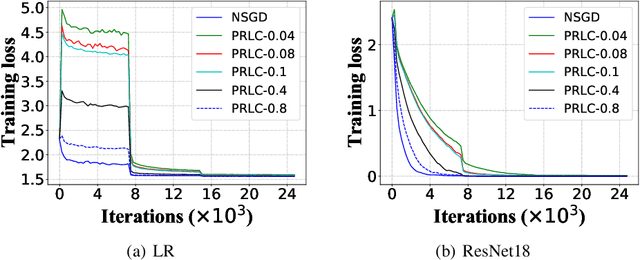
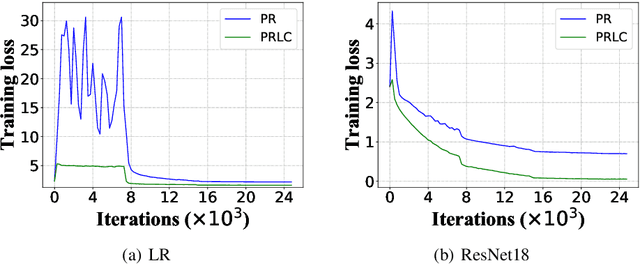
Federated Learning is a powerful machine learning paradigm to cooperatively train a global model with highly distributed data. A major bottleneck on the performance of distributed Stochastic Gradient Descent (SGD) algorithm for large-scale Federated Learning is the communication overhead on pushing local gradients and pulling global model. In this paper, to reduce the communication complexity of Federated Learning, a novel approach named Pulling Reduction with Local Compensation (PRLC) is proposed. Specifically, each training node intermittently pulls the global model from the server in SGD iterations, resulting in that it is sometimes unsynchronized with the server. In such a case, it will use its local update to compensate the gap between the local model and the global model. Our rigorous theoretical analysis of PRLC achieves two important findings. First, we prove that the convergence rate of PRLC preserves the same order as the classical synchronous SGD for both strongly-convex and non-convex cases with good scalability due to the linear speedup with respect to the number of training nodes. Second, we show that PRLC admits lower pulling frequency than the existing pulling reduction method without local compensation. We also conduct extensive experiments on various machine learning models to validate our theoretical results. Experimental results show that our approach achieves a significant pulling reduction over the state-of-the-art methods, e.g., PRLC requiring only half of the pulling operations of LAG.