Intermittent Pulling with Local Compensation for Communication-Efficient Federated Learning
Paper and Code
Jan 22, 2020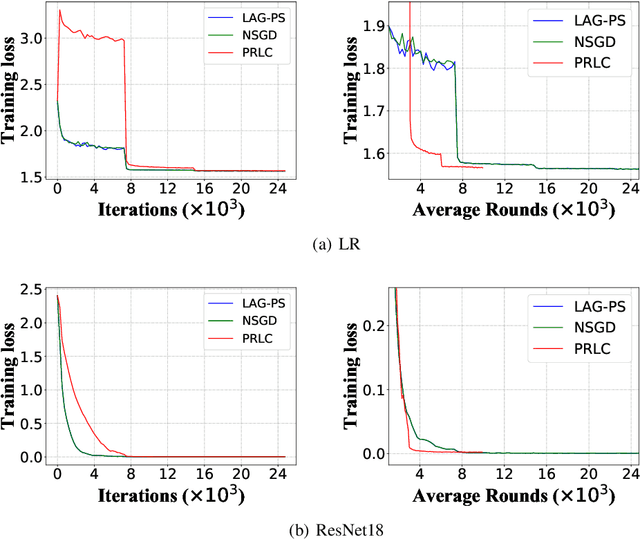
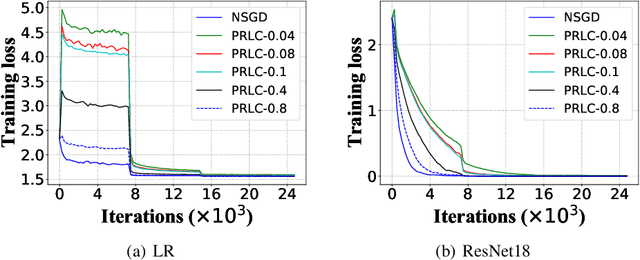
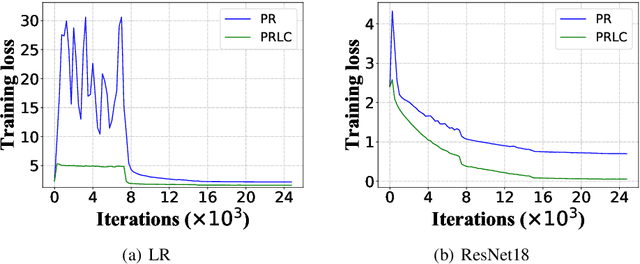

Federated Learning is a powerful machine learning paradigm to cooperatively train a global model with highly distributed data. A major bottleneck on the performance of distributed Stochastic Gradient Descent (SGD) algorithm for large-scale Federated Learning is the communication overhead on pushing local gradients and pulling global model. In this paper, to reduce the communication complexity of Federated Learning, a novel approach named Pulling Reduction with Local Compensation (PRLC) is proposed. Specifically, each training node intermittently pulls the global model from the server in SGD iterations, resulting in that it is sometimes unsynchronized with the server. In such a case, it will use its local update to compensate the gap between the local model and the global model. Our rigorous theoretical analysis of PRLC achieves two important findings. First, we prove that the convergence rate of PRLC preserves the same order as the classical synchronous SGD for both strongly-convex and non-convex cases with good scalability due to the linear speedup with respect to the number of training nodes. Second, we show that PRLC admits lower pulling frequency than the existing pulling reduction method without local compensation. We also conduct extensive experiments on various machine learning models to validate our theoretical results. Experimental results show that our approach achieves a significant pulling reduction over the state-of-the-art methods, e.g., PRLC requiring only half of the pulling operations of LAG.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge