The Role of Depth, Width, and Tree Size in Expressiveness of Deep Forest

Random forests are classical ensemble algorithms that construct multiple randomized decision trees and aggregate their predictions using naive averaging. \citet{zhou2019deep} further propose a deep forest algorithm with multi-layer forests, which outperforms random forests in various tasks. The performance of deep forests is related to three hyperparameters in practice: depth, width, and tree size, but little has been known about its theoretical explanation. This work provides the first upper and lower bounds on the approximation complexity of deep forests concerning the three hyperparameters. Our results confirm the distinctive role of depth, which can exponentially enhance the expressiveness of deep forests compared with width and tree size. Experiments confirm the theoretical findings.

On the Approximation and Complexity of Deep Neural Networks to Invariant Functions

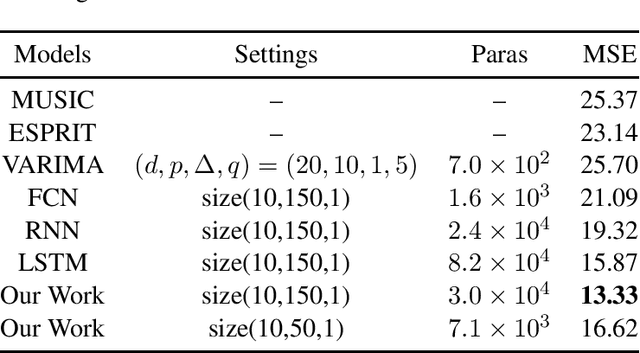
Recent years have witnessed a hot wave of deep neural networks in various domains; however, it is not yet well understood theoretically. A theoretical characterization of deep neural networks should point out their approximation ability and complexity, i.e., showing which architecture and size are sufficient to handle the concerned tasks. This work takes one step on this direction by theoretically studying the approximation and complexity of deep neural networks to invariant functions. We first prove that the invariant functions can be universally approximated by deep neural networks. Then we show that a broad range of invariant functions can be asymptotically approximated by various types of neural network models that includes the complex-valued neural networks, convolutional neural networks, and Bayesian neural networks using a polynomial number of parameters or optimization iterations. We also provide a feasible application that connects the parameter estimation and forecasting of high-resolution signals with our theoretical conclusions. The empirical results obtained on simulation experiments demonstrate the effectiveness of our method.

Towards Theoretical Understanding of Flexible Transmitter Networks via Approximation and Local Minima

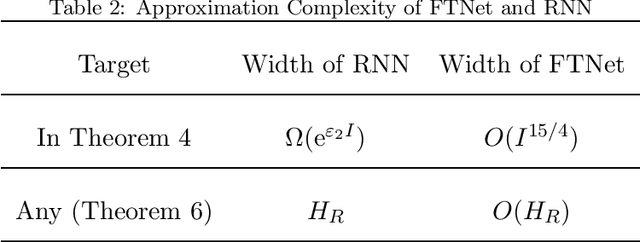
Flexible Transmitter Network (FTNet) is a recently proposed bio-plausible neural network and has achieved competitive performance with the state-of-the-art models when handling temporal-spatial data. However, there remains an open problem about the theoretical understanding of FTNet. This work investigates the theoretical properties of one-hidden-layer FTNet from the perspectives of approximation and local minima. Under mild assumptions, we show that: i) FTNet is a universal approximator; ii) the approximation complexity of FTNet can be exponentially smaller than those of real-valued neural networks with feedforward/recurrent architectures and is of the same order in the worst case; iii) any local minimum of FTNet is the global minimum, which suggests that it is possible for local search algorithms to converge to the global minimum. Our theoretical results indicate that FTNet can efficiently express target functions and has no concern about local minima, which complements the theoretical blank of FTNet and exhibits the possibility for ameliorating the FTNet.