Towards Theoretical Understanding of Flexible Transmitter Networks via Approximation and Local Minima
Paper and Code
Nov 11, 2021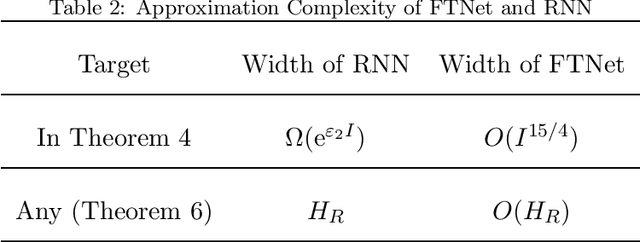
Flexible Transmitter Network (FTNet) is a recently proposed bio-plausible neural network and has achieved competitive performance with the state-of-the-art models when handling temporal-spatial data. However, there remains an open problem about the theoretical understanding of FTNet. This work investigates the theoretical properties of one-hidden-layer FTNet from the perspectives of approximation and local minima. Under mild assumptions, we show that: i) FTNet is a universal approximator; ii) the approximation complexity of FTNet can be exponentially smaller than those of real-valued neural networks with feedforward/recurrent architectures and is of the same order in the worst case; iii) any local minimum of FTNet is the global minimum, which suggests that it is possible for local search algorithms to converge to the global minimum. Our theoretical results indicate that FTNet can efficiently express target functions and has no concern about local minima, which complements the theoretical blank of FTNet and exhibits the possibility for ameliorating the FTNet.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge