Horizon-wise Learning Paradigm Promotes Gene Splicing Identification

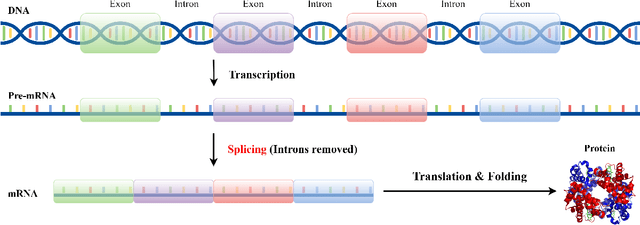
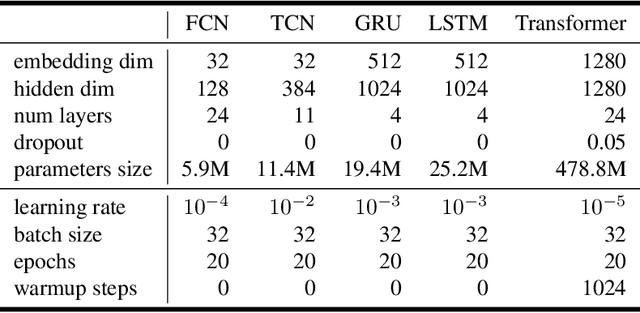
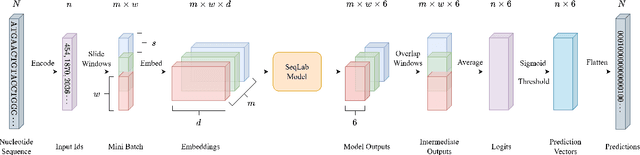
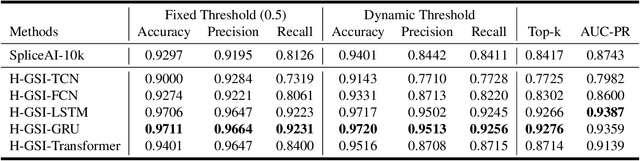
Identifying gene splicing is a core and significant task confronted in modern collaboration between artificial intelligence and bioinformatics. Past decades have witnessed great efforts on this concern, such as the bio-plausible splicing pattern AT-CG and the famous SpliceAI. In this paper, we propose a novel framework for the task of gene splicing identification, named Horizon-wise Gene Splicing Identification (H-GSI). The proposed H-GSI follows the horizon-wise identification paradigm and comprises four components: the pre-processing procedure transforming string data into tensors, the sliding window technique handling long sequences, the SeqLab model, and the predictor. In contrast to existing studies that process gene information with a truncated fixed-length sequence, H-GSI employs a horizon-wise identification paradigm in which all positions in a sequence are predicted with only one forward computation, improving accuracy and efficiency. The experiments conducted on the real-world Human dataset show that our proposed H-GSI outperforms SpliceAI and achieves the best accuracy of 97.20\%. The source code is available from this link.

A Unified Kernel for Neural Network Learning

Past decades have witnessed a great interest in the distinction and connection between neural network learning and kernel learning. Recent advancements have made theoretical progress in connecting infinite-wide neural networks and Gaussian processes. Two predominant approaches have emerged: the Neural Network Gaussian Process (NNGP) and the Neural Tangent Kernel (NTK). The former, rooted in Bayesian inference, represents a zero-order kernel, while the latter, grounded in the tangent space of gradient descents, is a first-order kernel. In this paper, we present the Unified Neural Kernel (UNK), which characterizes the learning dynamics of neural networks with gradient descents and parameter initialization. The proposed UNK kernel maintains the limiting properties of both NNGP and NTK, exhibiting behaviors akin to NTK with a finite learning step and converging to NNGP as the learning step approaches infinity. Besides, we also theoretically characterize the uniform tightness and learning convergence of the UNK kernel, providing comprehensive insights into this unified kernel. Experimental results underscore the effectiveness of our proposed method.

On the Approximation and Complexity of Deep Neural Networks to Invariant Functions

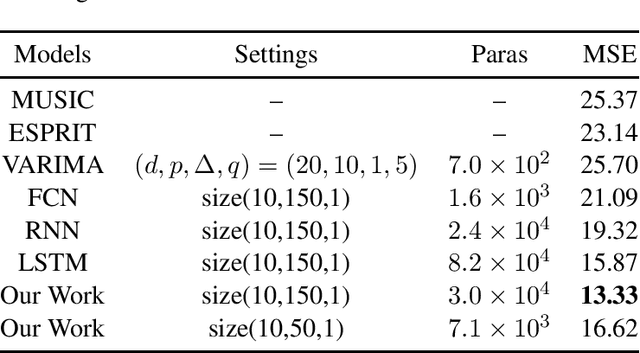
Recent years have witnessed a hot wave of deep neural networks in various domains; however, it is not yet well understood theoretically. A theoretical characterization of deep neural networks should point out their approximation ability and complexity, i.e., showing which architecture and size are sufficient to handle the concerned tasks. This work takes one step on this direction by theoretically studying the approximation and complexity of deep neural networks to invariant functions. We first prove that the invariant functions can be universally approximated by deep neural networks. Then we show that a broad range of invariant functions can be asymptotically approximated by various types of neural network models that includes the complex-valued neural networks, convolutional neural networks, and Bayesian neural networks using a polynomial number of parameters or optimization iterations. We also provide a feasible application that connects the parameter estimation and forecasting of high-resolution signals with our theoretical conclusions. The empirical results obtained on simulation experiments demonstrate the effectiveness of our method.

Towards Theoretical Understanding of Flexible Transmitter Networks via Approximation and Local Minima

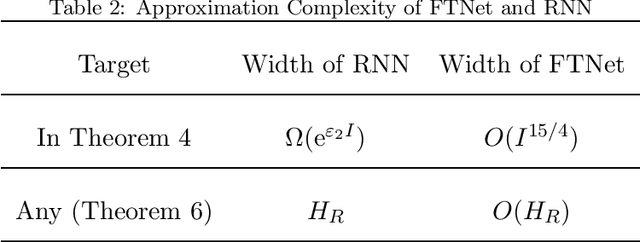
Flexible Transmitter Network (FTNet) is a recently proposed bio-plausible neural network and has achieved competitive performance with the state-of-the-art models when handling temporal-spatial data. However, there remains an open problem about the theoretical understanding of FTNet. This work investigates the theoretical properties of one-hidden-layer FTNet from the perspectives of approximation and local minima. Under mild assumptions, we show that: i) FTNet is a universal approximator; ii) the approximation complexity of FTNet can be exponentially smaller than those of real-valued neural networks with feedforward/recurrent architectures and is of the same order in the worst case; iii) any local minimum of FTNet is the global minimum, which suggests that it is possible for local search algorithms to converge to the global minimum. Our theoretical results indicate that FTNet can efficiently express target functions and has no concern about local minima, which complements the theoretical blank of FTNet and exhibits the possibility for ameliorating the FTNet.

ARISE: ApeRIodic SEmi-parametric Process for Efficient Markets without Periodogram and Gaussianity Assumptions

Mimicking and learning the long-term memory of efficient markets is a fundamental problem in the interaction between machine learning and financial economics to sequential data. Despite the prominence of this issue, current treatments either remain largely limited to heuristic techniques or rely significantly on periodogram or Gaussianty assumptions. In this paper, we present the ApeRIodic SEmi-parametric (ARISE) process for investigating efficient markets. The ARISE process is formulated as an infinite-sum function of some known processes and employs the aperiodic spectrum estimation to determine the key hyper-parameters, thus possessing the power and potential of modeling the price data with long-term memory, non-stationarity, and aperiodic spectrum. We further theoretically show that the ARISE process has the mean-square convergence, consistency, and asymptotic normality without periodogram and Gaussianity assumptions. In practice, we apply the ARISE process to identify the efficiency of real-world markets. Besides, we also provide two alternative ARISE applications: studying the long-term memorability of various machine-learning models and developing a latent state-space model for inference and forecasting of time series. The numerical experiments confirm the superiority of our proposed approaches.

LIFE: Learning Individual Features for Multivariate Time Series Prediction with Missing Values

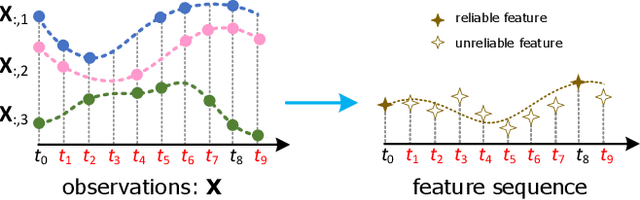
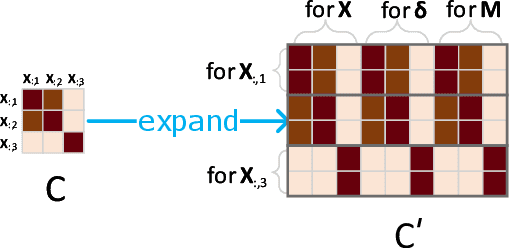
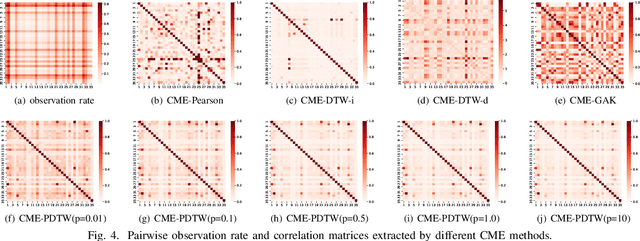
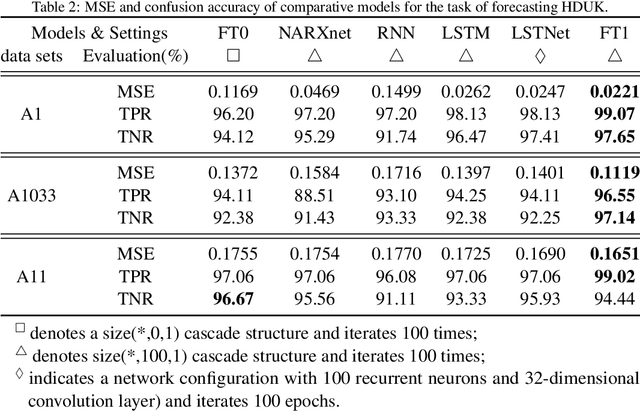
Multivariate time series (MTS) prediction is ubiquitous in real-world fields, but MTS data often contains missing values. In recent years, there has been an increasing interest in using end-to-end models to handle MTS with missing values. To generate features for prediction, existing methods either merge all input dimensions of MTS or tackle each input dimension independently. However, both approaches are hard to perform well because the former usually produce many unreliable features and the latter lacks correlated information. In this paper, we propose a Learning Individual Features (LIFE) framework, which provides a new paradigm for MTS prediction with missing values. LIFE generates reliable features for prediction by using the correlated dimensions as auxiliary information and suppressing the interference from uncorrelated dimensions with missing values. Experiments on three real-world data sets verify the superiority of LIFE to existing state-of-the-art models.

Neural Network Gaussian Processes by Increasing Depth

Recent years have witnessed an increasing interest in the correspondence between infinitely wide networks and Gaussian processes. Despite the effectiveness and elegance of the current neural network Gaussian process theory, to the best of our knowledge, all the neural network Gaussian processes are essentially induced by increasing width. However, in the era of deep learning, what concerns us more regarding a neural network is its depth as well as how depth impacts the behaviors of a network. Inspired by a width-depth symmetry consideration, we use a shortcut network to show that increasing the depth of a neural network can also give rise to a Gaussian process, which is a valuable addition to the existing theory and contributes to revealing the true picture of deep learning. Beyond the proposed Gaussian process by depth, we theoretically characterize its uniform tightness property and the smallest eigenvalue of its associated kernel. These characterizations can not only enhance our understanding of the proposed depth-induced Gaussian processes, but also pave the way for future applications. Lastly, we examine the performance of the proposed Gaussian process by regression experiments on two real-world data sets.

Towards Understanding Theoretical Advantages of Complex-Reaction Networks

Complex-valued neural networks have attracted increasing attention in recent years, while it remains open on the advantages of complex-valued neural networks in comparison with real-valued networks. This work takes one step on this direction by introducing the \emph{complex-reaction network} with fully-connected feed-forward architecture. We prove the universal approximation property for complex-reaction networks, and show that a class of radial functions can be approximated by a complex-reaction network using the polynomial number of parameters, whereas real-valued networks need at least exponential parameters to reach the same approximation level. For empirical risk minimization, our theoretical result shows that the critical point set of complex-reaction networks is a proper subset of that of real-valued networks, which may show some insights on finding the optimal solutions more easily for complex-reaction networks.

Flexible Transmitter Network

Current neural networks are mostly built upon the MP model, which usually formulates the neuron as executing an activation function on the real-valued weighted aggregation of signals received from other neurons. In this paper, we propose the Flexible Transmitter (FT) model, a novel bio-plausible neuron with flexible plasticity. The FT model employs a pair of parameters to model the transmitter between neurons and sets up a neurotransmitter regulated memory unit to record the long-term learning information of the concerned neuron, thus leading to the formulation of the FT model as a two-variable two-valued function, which takes the commonly-used MP neuron model as its special case. The FT model can handle more complicated data, even time series signals. To exhibit the power and potential of our FT model, we present the Flexible Transmitter Network (FTNet), which is built in the most common fully-connected feed-forward architecture by incorporating the FT neuron as the basic building block. FTNet allows gradient calculation and can be implemented by an extension of the backpropagation algorithm in the complex domain. Experiments on a board range of tasks show the superiority of the proposed FTNet. This study provides an alternative basic building block in neural networks and exhibits the feasibility of developing artificial neural networks with neuronal plasticity.

Bifurcation Spiking Neural Network

Recently spiking neural networks (SNNs) have received much attention because of its rich biological significance and its power in processing spatial and temporal information. However, most existing SNNs are static due to the fixed eigenvalues of spiking generation functions, which means that neurons fire spikes in a fixed frequency when receiving constant input signals. Thereby, the static SNNs are limited in scalability. In this paper, we clarify the bifurcation relationship that dynamic eigenvalues have a great influence on the neuron excitation frequency. And then we propose the Bifurcation Spiking Neural Network (BSNN) for developing a dynamic SNN. Different from traditional static SNNs, BSNN takes a bifurcation system with time-varying eigenvalues as the basic building block, thus it has more powerful flexibility and is able to handle data with complex nonlinear structures. Experiments on wide-range tasks have been conducted, including a delayed-memory XOR task, four image recognition datasets, and 25 UCR archive. The results show that the performance of BSNN is superior to the existing static SNN models.