LoRA Dropout as a Sparsity Regularizer for Overfitting Control

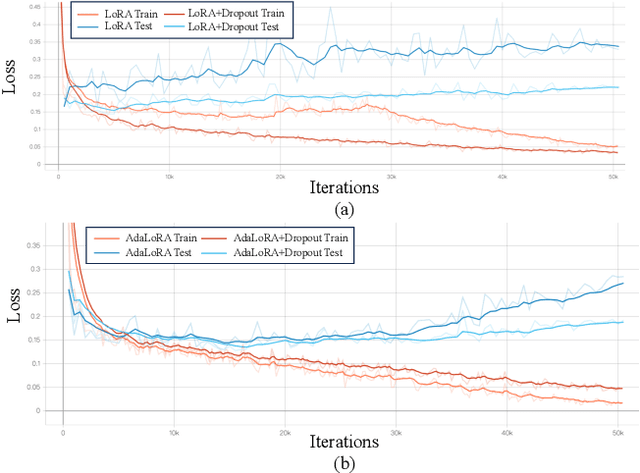
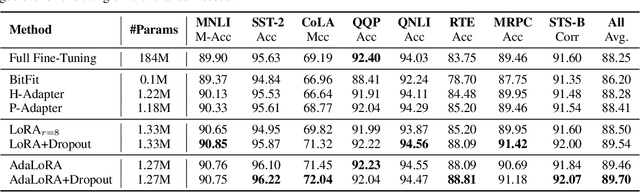
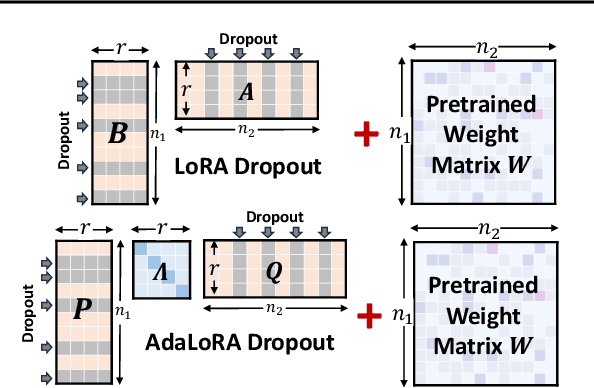
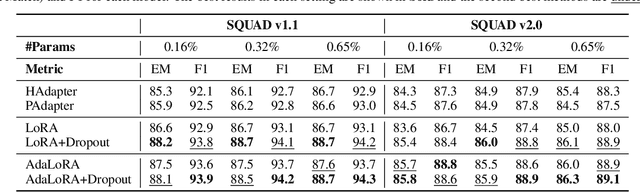
Parameter-efficient fine-tuning methods, represented by LoRA, play an essential role in adapting large-scale pre-trained models to downstream tasks. However, fine-tuning LoRA-series models also faces the risk of overfitting on the training dataset, and yet there's still a lack of theoretical guidance and practical mechanism to control overfitting on LoRA-based PEFT methods. In this paper, we propose a LoRA Dropout mechanism for the LoRA-based methods by introducing random noises to the learnable low-rank matrices and increasing parameter sparsity. We then demonstrate the theoretical mechanism of our LoRA Dropout mechanism from the perspective of sparsity regularization by providing a generalization error bound under this framework. Theoretical results show that appropriate sparsity would help tighten the gap between empirical and generalization risks and thereby control overfitting. Furthermore, based on the LoRA Dropout framework, we introduce a test-time ensemble strategy and provide theoretical evidence demonstrating that the ensemble method can further compress the error bound, and lead to better performance during inference time. Extensive experiments on various NLP tasks provide practical validations of the effectiveness of our LoRA Dropout framework in improving model accuracy and calibration.

Parameter Efficient Quasi-Orthogonal Fine-Tuning via Givens Rotation

With the increasingly powerful performances and enormous scales of Pretrained Language Models (PLMs), promoting parameter efficiency in fine-tuning has become a crucial need for effective and efficient adaptation to various downstream tasks. One representative line of fine-tuning methods is Orthogonal Fine-tuning (OFT), which rigorously preserves the angular distances within the parameter space to preserve the pretrained knowledge. Despite the empirical effectiveness, OFT still suffers low parameter efficiency at $\mathcal{O}(d^2)$ and limited capability of downstream adaptation. Inspired by Givens rotation, in this paper, we proposed quasi-Givens Orthogonal Fine-Tuning (qGOFT) to address the problems. We first use $\mathcal{O}(d)$ Givens rotations to accomplish arbitrary orthogonal transformation in $SO(d)$ with provable equivalence, reducing parameter complexity from $\mathcal{O}(d^2)$ to $\mathcal{O}(d)$. Then we introduce flexible norm and relative angular adjustments under soft orthogonality regularization to enhance the adaptation capability of downstream semantic deviations. Extensive experiments on various tasks and PLMs validate the effectiveness of our methods.

Boosting Semi-Supervised Learning with Contrastive Complementary Labeling

Semi-supervised learning (SSL) has achieved great success in leveraging a large amount of unlabeled data to learn a promising classifier. A popular approach is pseudo-labeling that generates pseudo labels only for those unlabeled data with high-confidence predictions. As for the low-confidence ones, existing methods often simply discard them because these unreliable pseudo labels may mislead the model. Nevertheless, we highlight that these data with low-confidence pseudo labels can be still beneficial to the training process. Specifically, although the class with the highest probability in the prediction is unreliable, we can assume that this sample is very unlikely to belong to the classes with the lowest probabilities. In this way, these data can be also very informative if we can effectively exploit these complementary labels, i.e., the classes that a sample does not belong to. Inspired by this, we propose a novel Contrastive Complementary Labeling (CCL) method that constructs a large number of reliable negative pairs based on the complementary labels and adopts contrastive learning to make use of all the unlabeled data. Extensive experiments demonstrate that CCL significantly improves the performance on top of existing methods. More critically, our CCL is particularly effective under the label-scarce settings. For example, we yield an improvement of 2.43% over FixMatch on CIFAR-10 only with 40 labeled data.