Quantifying Preferences of Vision-Language Models via Value Decomposition in Social Media Contexts

The rapid advancement of Vision-Language Models (VLMs) has expanded multimodal applications, yet evaluations often focus on basic tasks like object recognition, overlooking abstract aspects such as personalities and values. To address this gap, we introduce Value-Spectrum, a visual question-answering benchmark aimed at assessing VLMs based on Schwartz's value dimensions, which capture core values guiding people's beliefs and actions across cultures. We constructed a vectorized database of over 50,000 short videos sourced from TikTok, YouTube Shorts, and Instagram Reels, covering multiple months and a wide array of topics such as family, health, hobbies, society, and technology. We also developed a VLM agent pipeline to automate video browsing and analysis. Benchmarking representative VLMs on Value-Spectrum reveals significant differences in their responses to value-oriented content, with most models exhibiting a preference for hedonistic topics. Beyond identifying natural preferences, we explored the ability of VLM agents to adopt specific personas when explicitly prompted, revealing insights into the models' adaptability in role-playing scenarios. These findings highlight the potential of Value-Spectrum as a comprehensive evaluation set for tracking VLM advancements in value-based tasks and for developing more sophisticated role-playing AI agents.

TimeAutoDiff: Combining Autoencoder and Diffusion model for time series tabular data synthesizing

In this paper, we leverage the power of latent diffusion models to generate synthetic time series tabular data. Along with the temporal and feature correlations, the heterogeneous nature of the feature in the table has been one of the main obstacles in time series tabular data modeling. We tackle this problem by combining the ideas of the variational auto-encoder (VAE) and the denoising diffusion probabilistic model (DDPM). Our model named as \texttt{TimeAutoDiff} has several key advantages including (1) Generality: the ability to handle the broad spectrum of time series tabular data from single to multi-sequence datasets; (2) Good fidelity and utility guarantees: numerical experiments on six publicly available datasets demonstrating significant improvements over state-of-the-art models in generating time series tabular data, across four metrics measuring fidelity and utility; (3) Fast sampling speed: entire time series data generation as opposed to the sequential data sampling schemes implemented in the existing diffusion-based models, eventually leading to significant improvements in sampling speed, (4) Entity conditional generation: the first implementation of conditional generation of multi-sequence time series tabular data with heterogenous features in the literature, enabling scenario exploration across multiple scientific and engineering domains. Codes are in preparation for release to the public, but available upon request.

SA-FedLora: Adaptive Parameter Allocation for Efficient Federated Learning with LoRA Tuning

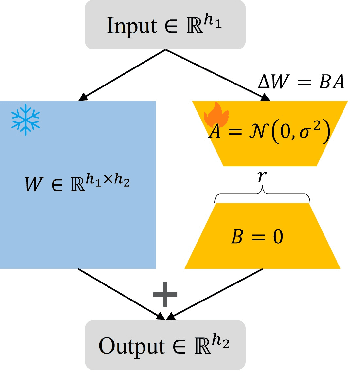
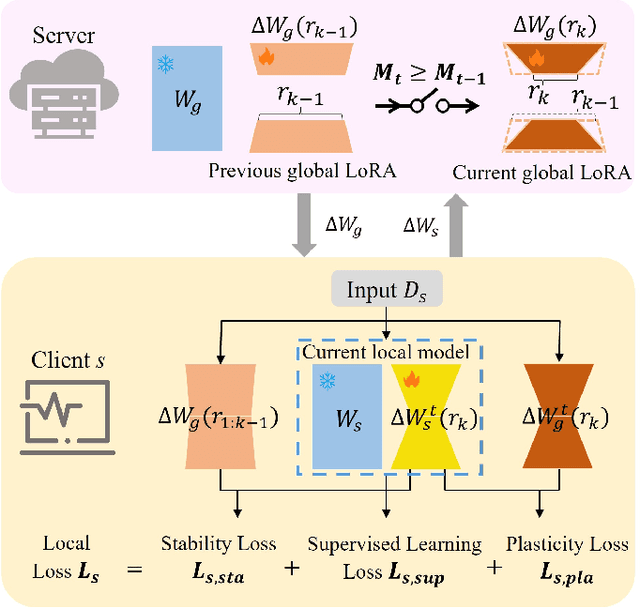
Fine-tuning large-scale pre-trained models via transfer learning is an emerging important paradigm for a wide range of downstream tasks, with performance heavily reliant on extensive data. Federated learning (FL), as a distributed framework, provides a secure solution to train models on local datasets while safeguarding raw sensitive data. However, FL networks encounter high communication costs due to the massive parameters of large-scale pre-trained models, necessitating parameter-efficient methods. Notably, parameter efficient fine tuning, such as Low-Rank Adaptation (LoRA), has shown remarkable success in fine-tuning pre-trained models. However, prior research indicates that the fixed parameter budget may be prone to the overfitting or slower convergence. To address this challenge, we propose a Simulated Annealing-based Federated Learning with LoRA tuning (SA-FedLoRA) approach by reducing trainable parameters. Specifically, SA-FedLoRA comprises two stages: initiating and annealing. (1) In the initiating stage, we implement a parameter regularization approach during the early rounds of aggregation, aiming to mitigate client drift and accelerate the convergence for the subsequent tuning. (2) In the annealing stage, we allocate higher parameter budget during the early 'heating' phase and then gradually shrink the budget until the 'cooling' phase. This strategy not only facilitates convergence to the global optimum but also reduces communication costs. Experimental results demonstrate that SA-FedLoRA is an efficient FL, achieving superior performance to FedAvg and significantly reducing communication parameters by up to 93.62%.

On Finite-Step Convergence of the Non-Greedy Algorithm for $L_1$-Norm PCA and Beyond

The non-greedy algorithm for $L_1$-norm PCA proposed in \cite{nie2011robust} is revisited and its convergence properties are studied. The algorithm is first interpreted as a conditional subgradient or an alternating maximization method. By treating it as a conditional subgradient, the iterative points generated by the algorithm will not change in finitely many steps under a certain full-rank assumption; such an assumption can be removed when the projection dimension is one. By treating the algorithm as an alternating maximization, it is proved that the objective value will not change after at most $\left\lceil \frac{F^{\max}}{\tau_0} \right\rceil$ steps. The stopping point satisfies certain optimality conditions. Then, a variant algorithm with improved convergence properties is studied. The iterative points generated by the algorithm will not change after at most $\left\lceil \frac{2F^{\max}}{\tau} \right\rceil$ steps and the stopping point also satisfies certain optimality conditions given a small enough $\tau$. Similar finite-step convergence is also established for a slight modification of the PAMe proposed in \cite{wang2021linear} very recently under a full-rank assumption. Such an assumption can also be removed when the projection dimension is one.

Approximation Algorithms for Sparse Best Rank-1 Approximation to Higher-Order Tensors

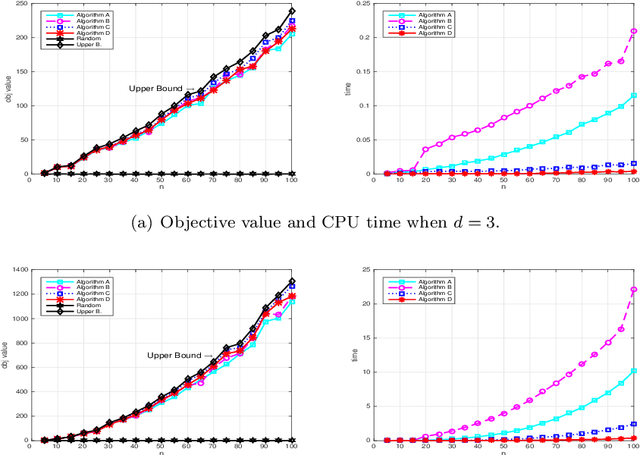
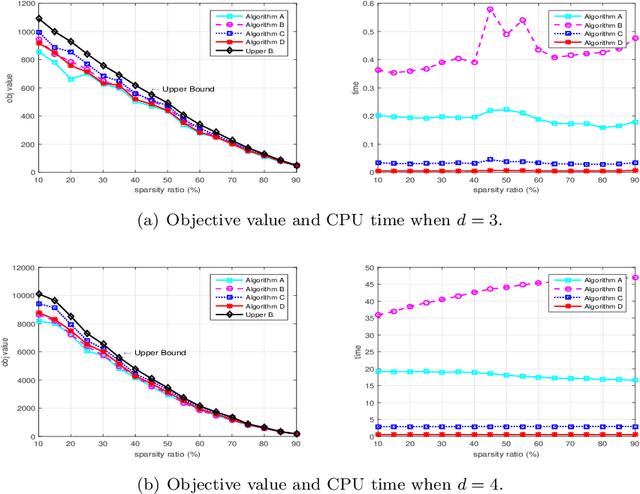
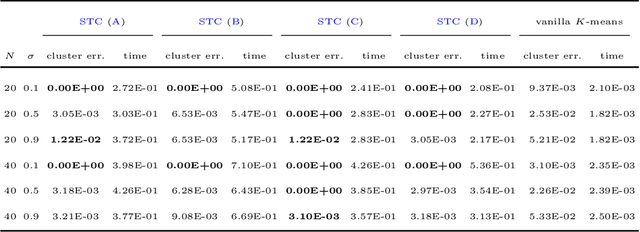
Sparse tensor best rank-1 approximation (BR1Approx), which is a sparsity generalization of the dense tensor BR1Approx, and is a higher-order extension of the sparse matrix BR1Approx, is one of the most important problems in sparse tensor decomposition and related problems arising from statistics and machine learning. By exploiting the multilinearity as well as the sparsity structure of the problem, four approximation algorithms are proposed, which are easily implemented, of low computational complexity, and can serve as initial procedures for iterative algorithms. In addition, theoretically guaranteed worst-case approximation lower bounds are proved for all the algorithms. We provide numerical experiments on synthetic and real data to illustrate the effectiveness of the proposed algorithms.

Higher order Matching Pursuit for Low Rank Tensor Learning

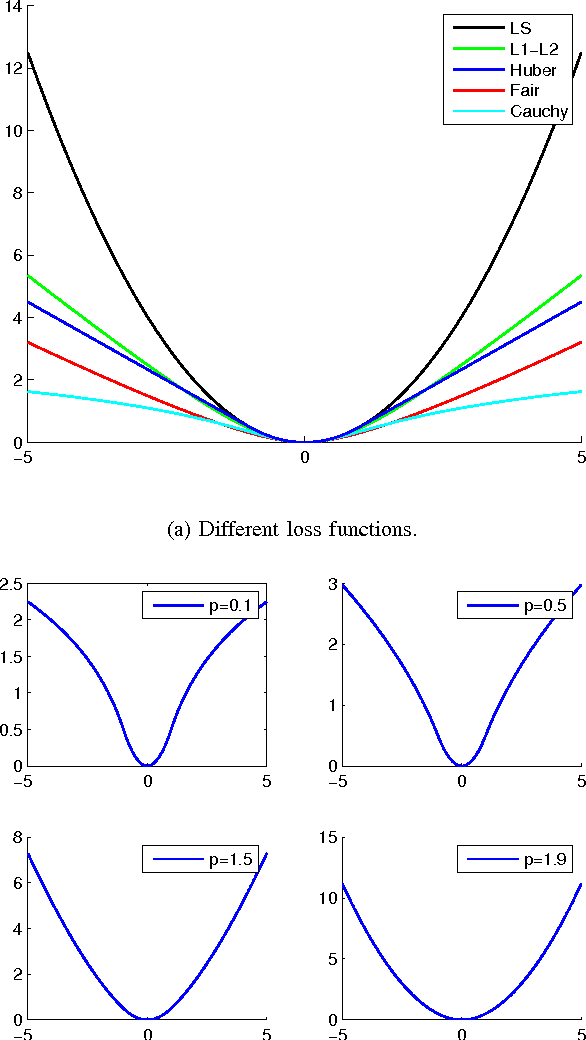
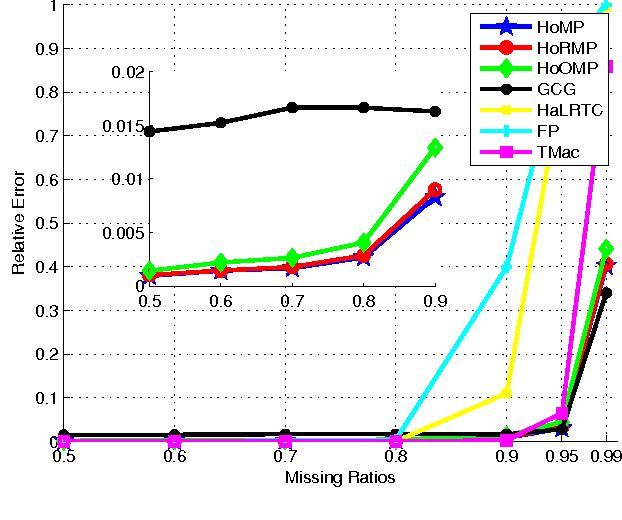
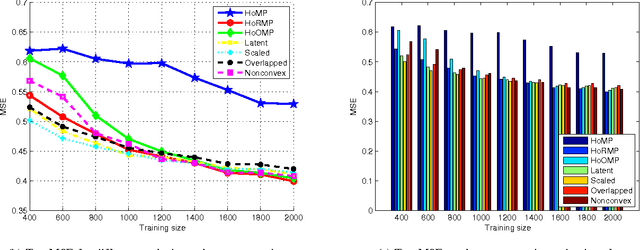
Low rank tensor learning, such as tensor completion and multilinear multitask learning, has received much attention in recent years. In this paper, we propose higher order matching pursuit for low rank tensor learning problems with a convex or a nonconvex cost function, which is a generalization of the matching pursuit type methods. At each iteration, the main cost of the proposed methods is only to compute a rank-one tensor, which can be done efficiently, making the proposed methods scalable to large scale problems. Moreover, storing the resulting rank-one tensors is of low storage requirement, which can help to break the curse of dimensionality. The linear convergence rate of the proposed methods is established in various circumstances. Along with the main methods, we also provide a method of low computational complexity for approximately computing the rank-one tensors, with provable approximation ratio, which helps to improve the efficiency of the main methods and to analyze the convergence rate. Experimental results on synthetic as well as real datasets verify the efficiency and effectiveness of the proposed methods.