Learning using granularity statistical invariants for classification

Learning using statistical invariants (LUSI) is a new learning paradigm, which adopts weak convergence mechanism, and can be applied to a wider range of classification problems. However, the computation cost of invariant matrices in LUSI is high for large-scale datasets during training. To settle this issue, this paper introduces a granularity statistical invariant for LUSI, and develops a new learning paradigm called learning using granularity statistical invariants (LUGSI). LUGSI employs both strong and weak convergence mechanisms, taking a perspective of minimizing expected risk. As far as we know, it is the first time to construct granularity statistical invariants. Compared to LUSI, the introduction of this new statistical invariant brings two advantages. Firstly, it enhances the structural information of the data. Secondly, LUGSI transforms a large invariant matrix into a smaller one by maximizing the distance between classes, achieving feasibility for large-scale datasets classification problems and significantly enhancing the training speed of model operations. Experimental results indicate that LUGSI not only exhibits improved generalization capabilities but also demonstrates faster training speed, particularly for large-scale datasets.

Least Squares Maximum and Weighted Generalization-Memorization Machines

In this paper, we propose a new way of remembering by introducing a memory influence mechanism for the least squares support vector machine (LSSVM). Without changing the equation constraints of the original LSSVM, this mechanism, allows an accurate partitioning of the training set without overfitting. The maximum memory impact model (MIMM) and the weighted impact memory model (WIMM) are then proposed. It is demonstrated that these models can be degraded to the LSSVM. Furthermore, we propose some different memory impact functions for the MIMM and WIMM. The experimental results show that that our MIMM and WIMM have better generalization performance compared to the LSSVM and significant advantage in time cost compared to other memory models.

Classification by estimating the cumulative distribution function for small data

In this paper, we study the classification problem by estimating the conditional probability function of the given data. Different from the traditional expected risk estimation theory on empirical data, we calculate the probability via Fredholm equation, this leads to estimate the distribution of the data. Based on the Fredholm equation, a new expected risk estimation theory by estimating the cumulative distribution function is presented. The main characteristics of the new expected risk estimation is to measure the risk on the distribution of the input space. The corresponding empirical risk estimation is also presented, and an $\varepsilon$-insensitive $L_{1}$ cumulative support vector machines ($\varepsilon$-$L_{1}VSVM$) is proposed by introducing an insensitive loss. It is worth mentioning that the classification models and the classification evaluation indicators based on the new mechanism are different from the traditional one. Experimental results show the effectiveness of the proposed $\varepsilon$-$L_{1}VSVM$ and the corresponding cumulative distribution function indicator on validity and interpretability of small data classification.

Generalization-Memorization Machines

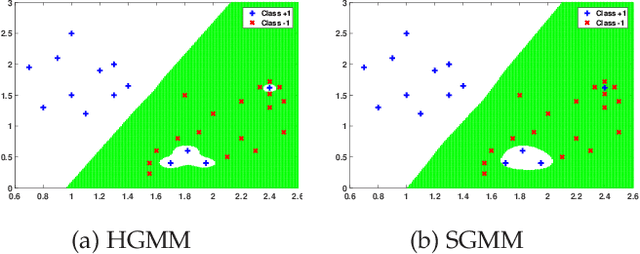
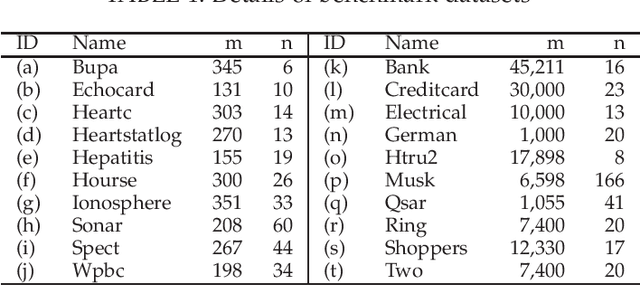
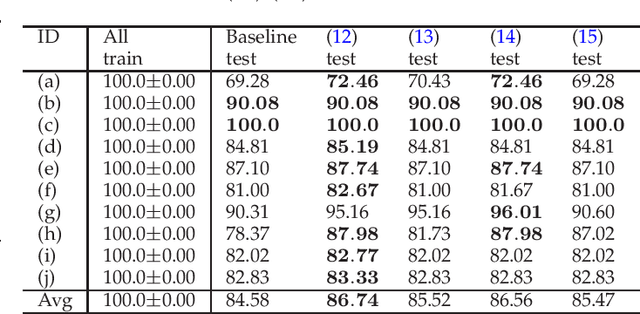
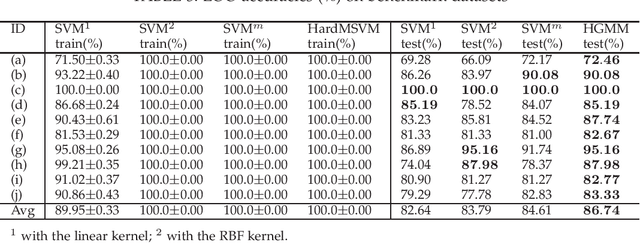
Classifying the training data correctly without over-fitting is one of the goals in machine learning. In this paper, we propose a generalization-memorization mechanism, including a generalization-memorization decision and a memory modeling principle. Under this mechanism, error-based learning machines improve their memorization abilities of training data without over-fitting. Specifically, the generalization-memorization machines (GMM) are proposed by applying this mechanism. The optimization problems in GMM are quadratic programming problems and could be solved efficiently. It should be noted that the recently proposed generalization-memorization kernel and the corresponding support vector machines are the special cases of our GMM. Experimental results show the effectiveness of the proposed GMM both on memorization and generalization.

Nonlinear Kernel Support Vector Machine with 0-1 Soft Margin Loss

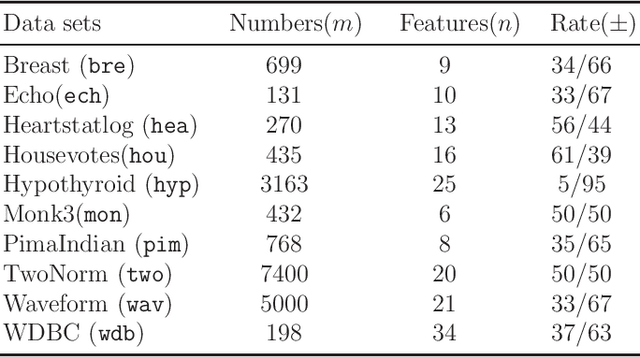
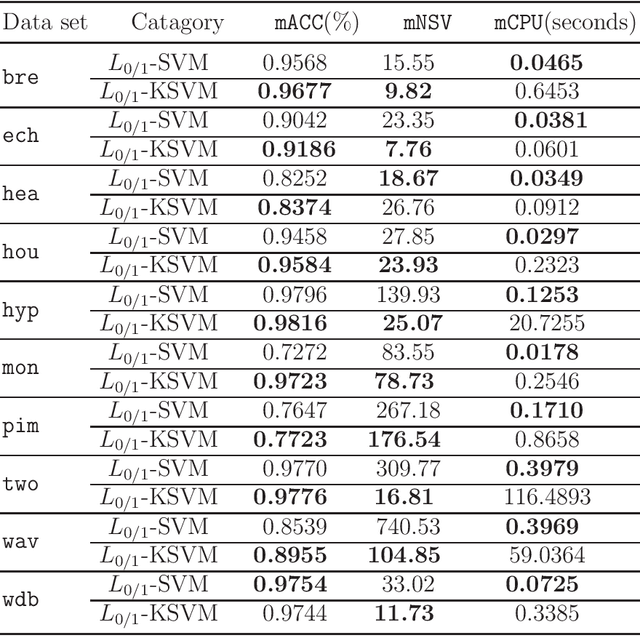
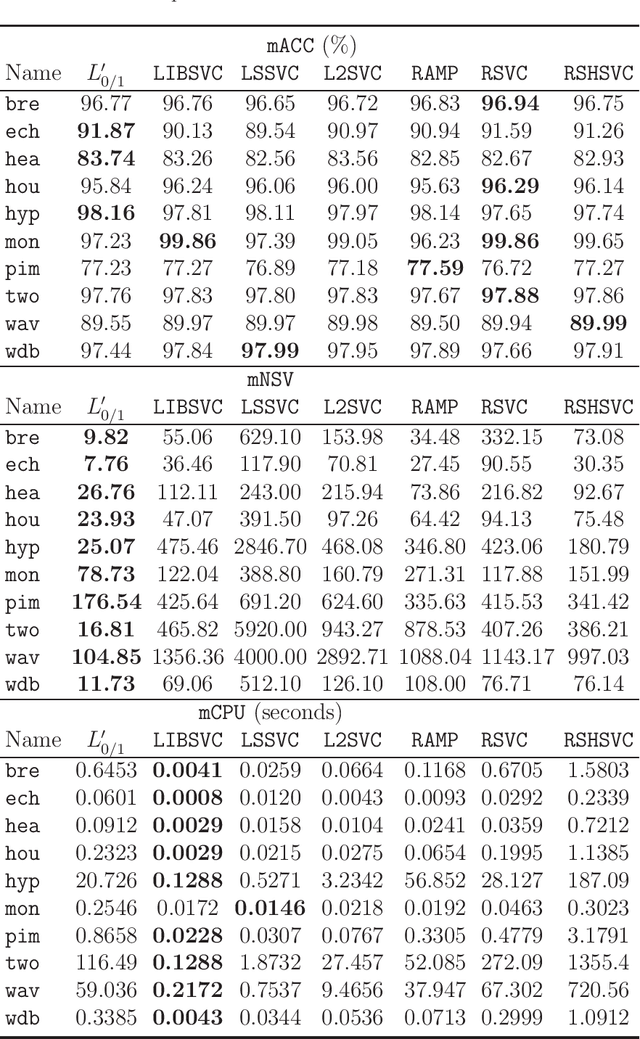
Recent advance on linear support vector machine with the 0-1 soft margin loss ($L_{0/1}$-SVM) shows that the 0-1 loss problem can be solved directly. However, its theoretical and algorithmic requirements restrict us extending the linear solving framework to its nonlinear kernel form directly, the absence of explicit expression of Lagrangian dual function of $L_{0/1}$-SVM is one big deficiency among of them. In this paper, by applying the nonparametric representation theorem, we propose a nonlinear model for support vector machine with 0-1 soft margin loss, called $L_{0/1}$-KSVM, which cunningly involves the kernel technique into it and more importantly, follows the success on systematically solving its linear task. Its optimal condition is explored theoretically and a working set selection alternating direction method of multipliers (ADMM) algorithm is introduced to acquire its numerical solution. Moreover, we firstly present a closed-form definition to the support vector (SV) of $L_{0/1}$-KSVM. Theoretically, we prove that all SVs of $L_{0/1}$-KSVM are only located on the parallel decision surfaces. The experiment part also shows that $L_{0/1}$-KSVM has much fewer SVs, simultaneously with a decent predicting accuracy, when comparing to its linear peer $L_{0/1}$-SVM and the other six nonlinear benchmark SVM classifiers.

Fuzzy Discriminant Clustering with Fuzzy Pairwise Constraints

In semi-supervised fuzzy clustering, this paper extends the traditional pairwise constraint (i.e., must-link or cannot-link) to fuzzy pairwise constraint. The fuzzy pairwise constraint allows a supervisor to provide the grade of similarity or dissimilarity between the implicit fuzzy vectors of a pair of samples. This constraint can present more complicated relationship between the pair of samples and avoid eliminating the fuzzy characteristics. We propose a fuzzy discriminant clustering model (FDC) to fuse the fuzzy pairwise constraints. The nonconvex optimization problem in our FDC is solved by a modified expectation-maximization algorithm, involving to solve several indefinite quadratic programming problems (IQPPs). Further, a diagonal block coordinate decent (DBCD) algorithm is proposed for these IQPPs, whose stationary points are guaranteed, and the global solutions can be obtained under certain conditions. To suit for different applications, the FDC is extended into various metric spaces, e.g., the Reproducing Kernel Hilbert Space. Experimental results on several benchmark datasets and facial expression database demonstrate the outperformance of our FDC compared with some state-of-the-art clustering models.

Two-dimensional Bhattacharyya bound linear discriminant analysis with its applications

Recently proposed L2-norm linear discriminant analysis criterion via the Bhattacharyya error bound estimation (L2BLDA) is an effective improvement of linear discriminant analysis (LDA) for feature extraction. However, L2BLDA is only proposed to cope with vector input samples. When facing with two-dimensional (2D) inputs, such as images, it will lose some useful information, since it does not consider intrinsic structure of images. In this paper, we extend L2BLDA to a two-dimensional Bhattacharyya bound linear discriminant analysis (2DBLDA). 2DBLDA maximizes the matrix-based between-class distance which is measured by the weighted pairwise distances of class means and meanwhile minimizes the matrix-based within-class distance. The weighting constant between the between-class and within-class terms is determined by the involved data that makes the proposed 2DBLDA adaptive. In addition, the criterion of 2DBLDA is equivalent to optimizing an upper bound of the Bhattacharyya error. The construction of 2DBLDA makes it avoid the small sample size problem while also possess robustness, and can be solved through a simple standard eigenvalue decomposition problem. The experimental results on image recognition and face image reconstruction demonstrate the effectiveness of the proposed methods.

Capped norm linear discriminant analysis and its applications

Classical linear discriminant analysis (LDA) is based on squared Frobenious norm and hence is sensitive to outliers and noise. To improve the robustness of LDA, in this paper, we introduce capped l_{2,1}-norm of a matrix, which employs non-squared l_2-norm and "capped" operation, and further propose a novel capped l_{2,1}-norm linear discriminant analysis, called CLDA. Due to the use of capped l_{2,1}-norm, CLDA can effectively remove extreme outliers and suppress the effect of noise data. In fact, CLDA can be also viewed as a weighted LDA. CLDA is solved through a series of generalized eigenvalue problems with theoretical convergency. The experimental results on an artificial data set, some UCI data sets and two image data sets demonstrate the effectiveness of CLDA.

Principal Component Analysis Based on T$\ell_1$-norm Maximization

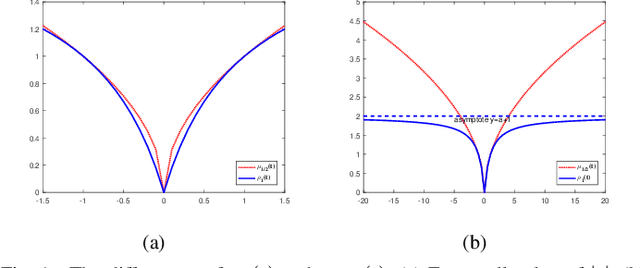
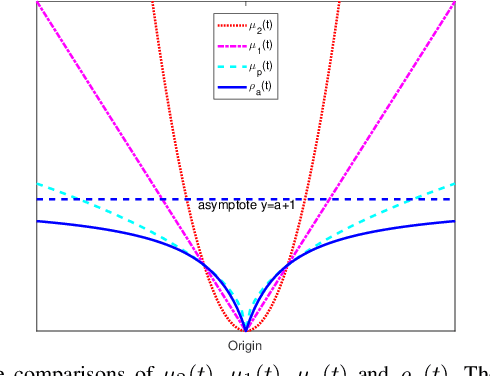
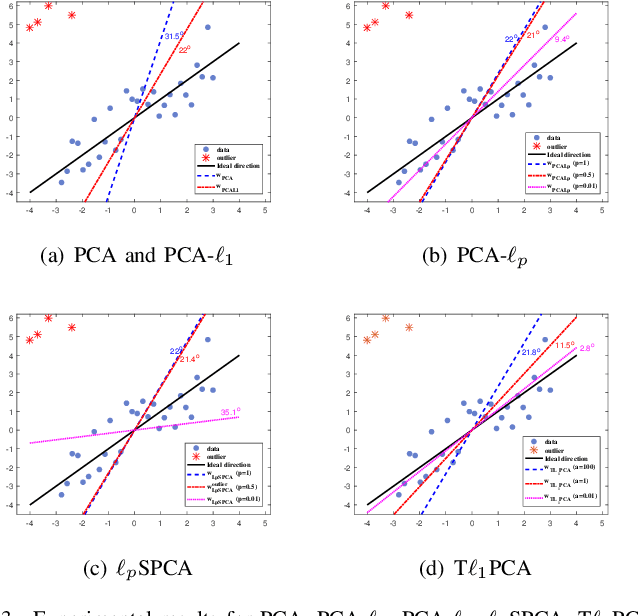
Classical principal component analysis (PCA) may suffer from the sensitivity to outliers and noise. Therefore PCA based on $\ell_1$-norm and $\ell_p$-norm ($0 < p < 1$) have been studied. Among them, the ones based on $\ell_p$-norm seem to be most interesting from the robustness point of view. However, their numerical performance is not satisfactory. Note that, although T$\ell_1$-norm is similar to $\ell_p$-norm ($0 < p < 1$) in some sense, it has the stronger suppression effect to outliers and better continuity. So PCA based on T$\ell_1$-norm is proposed in this paper. Our numerical experiments have shown that its performance is superior than PCA-$\ell_p$ and $\ell_p$SPCA as well as PCA, PCA-$\ell_1$ obviously.

Multiple Flat Projections for Cross-manifold Clustering

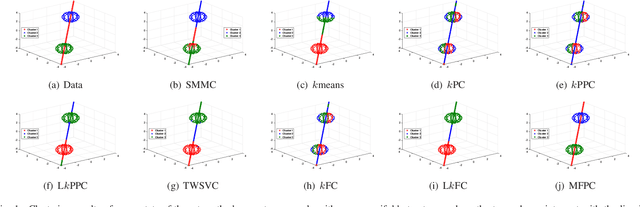
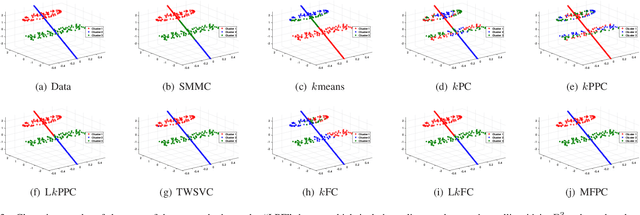
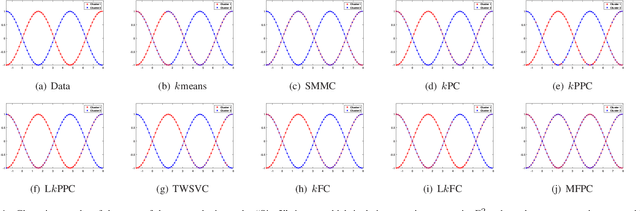
Cross-manifold clustering is a hard topic and many traditional clustering methods fail because of the cross-manifold structures. In this paper, we propose a Multiple Flat Projections Clustering (MFPC) to deal with cross-manifold clustering problems. In our MFPC, the given samples are projected into multiple subspaces to discover the global structures of the implicit manifolds. Thus, the cross-manifold clusters are distinguished from the various projections. Further, our MFPC is extended to nonlinear manifold clustering via kernel tricks to deal with more complex cross-manifold clustering. A series of non-convex matrix optimization problems in MFPC are solved by a proposed recursive algorithm. The synthetic tests show that our MFPC works on the cross-manifold structures well. Moreover, experimental results on the benchmark datasets show the excellent performance of our MFPC compared with some state-of-the-art clustering methods.