Nai-Yang Deng
Principal Component Analysis Based on T$\ell_1$-norm Maximization
May 23, 2020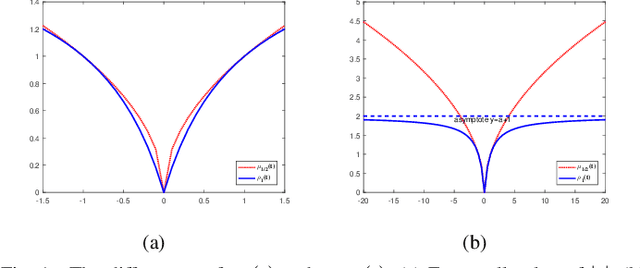
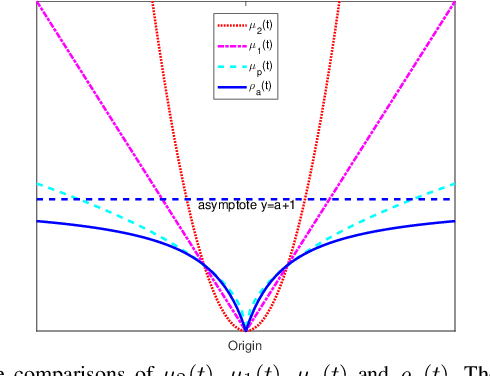
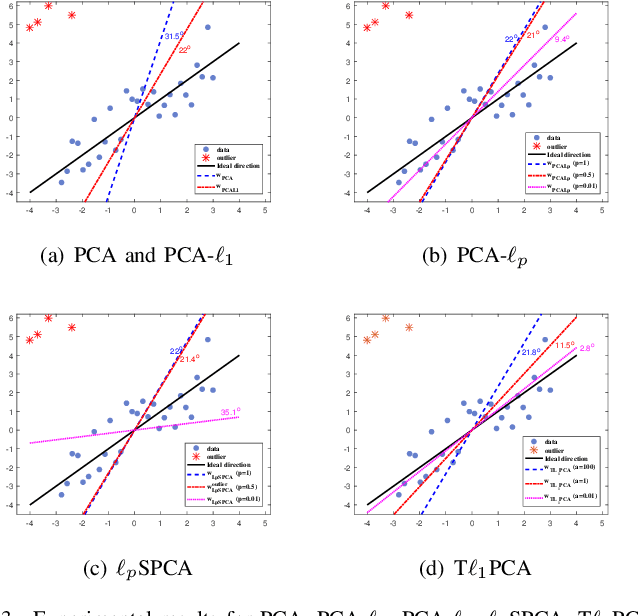

Abstract:Classical principal component analysis (PCA) may suffer from the sensitivity to outliers and noise. Therefore PCA based on $\ell_1$-norm and $\ell_p$-norm ($0 < p < 1$) have been studied. Among them, the ones based on $\ell_p$-norm seem to be most interesting from the robustness point of view. However, their numerical performance is not satisfactory. Note that, although T$\ell_1$-norm is similar to $\ell_p$-norm ($0 < p < 1$) in some sense, it has the stronger suppression effect to outliers and better continuity. So PCA based on T$\ell_1$-norm is proposed in this paper. Our numerical experiments have shown that its performance is superior than PCA-$\ell_p$ and $\ell_p$SPCA as well as PCA, PCA-$\ell_1$ obviously.
Multiple Flat Projections for Cross-manifold Clustering
Feb 17, 2020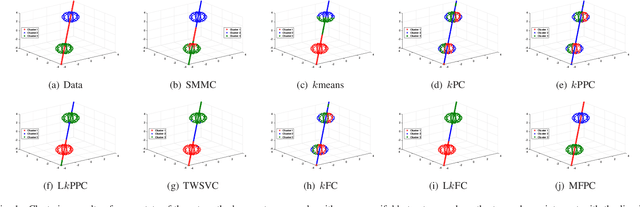

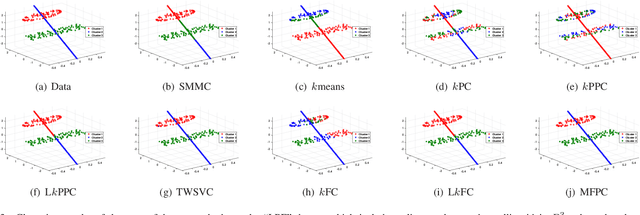
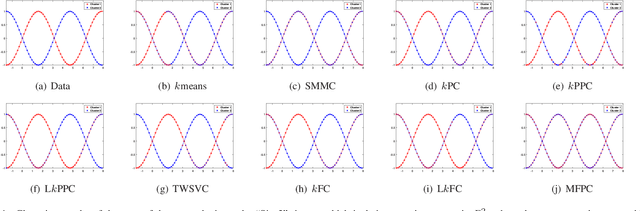
Abstract:Cross-manifold clustering is a hard topic and many traditional clustering methods fail because of the cross-manifold structures. In this paper, we propose a Multiple Flat Projections Clustering (MFPC) to deal with cross-manifold clustering problems. In our MFPC, the given samples are projected into multiple subspaces to discover the global structures of the implicit manifolds. Thus, the cross-manifold clusters are distinguished from the various projections. Further, our MFPC is extended to nonlinear manifold clustering via kernel tricks to deal with more complex cross-manifold clustering. A series of non-convex matrix optimization problems in MFPC are solved by a proposed recursive algorithm. The synthetic tests show that our MFPC works on the cross-manifold structures well. Moreover, experimental results on the benchmark datasets show the excellent performance of our MFPC compared with some state-of-the-art clustering methods.
Single Versus Union: Non-parallel Support Vector Machine Frameworks
Oct 22, 2019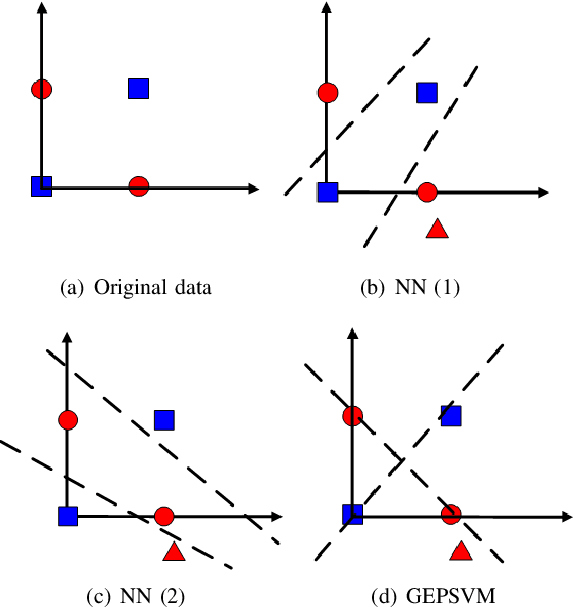
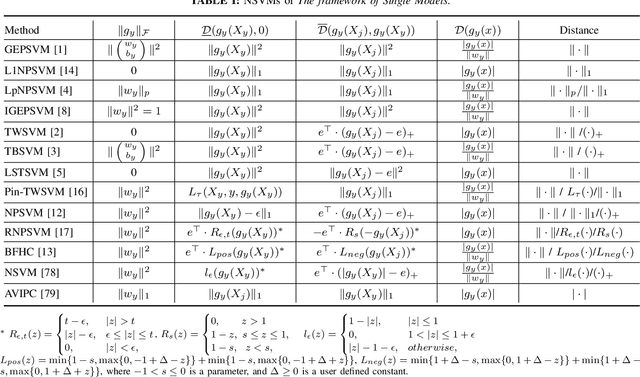

Abstract:Considering the classification problem, we summarize the nonparallel support vector machines with the nonparallel hyperplanes to two types of frameworks. The first type constructs the hyperplanes separately. It solves a series of small optimization problems to obtain a series of hyperplanes, but is hard to measure the loss of each sample. The other type constructs all the hyperplanes simultaneously, and it solves one big optimization problem with the ascertained loss of each sample. We give the characteristics of each framework and compare them carefully. In addition, based on the second framework, we construct a max-min distance-based nonparallel support vector machine for multiclass classification problem, called NSVM. It constructs hyperplanes with large distance margin by solving an optimization problem. Experimental results on benchmark data sets and human face databases show the advantages of our NSVM.
Robust Bhattacharyya bound linear discriminant analysis through adaptive algorithm
Nov 06, 2018



Abstract:In this paper, we propose a novel linear discriminant analysis criterion via the Bhattacharyya error bound estimation based on a novel L1-norm (L1BLDA) and L2-norm (L2BLDA). Both L1BLDA and L2BLDA maximize the between-class scatters which are measured by the weighted pairwise distances of class means and meanwhile minimize the within-class scatters under the L1-norm and L2-norm, respectively. The proposed models can avoid the small sample size (SSS) problem and have no rank limit that may encounter in LDA. It is worth mentioning that, the employment of L1-norm gives a robust performance of L1BLDA, and L1BLDA is solved through an effective non-greedy alternating direction method of multipliers (ADMM), where all the projection vectors can be obtained once for all. In addition, the weighting constants of L1BLDA and L2BLDA between the between-class and within-class terms are determined by the involved data set, which makes our L1BLDA and L2BLDA adaptive. The experimental results on both benchmark data sets as well as the handwritten digit databases demonstrate the effectiveness of the proposed methods.
Generalized two-dimensional linear discriminant analysis with regularization
Oct 25, 2018



Abstract:Recent advances show that two-dimensional linear discriminant analysis (2DLDA) is a successful matrix based dimensionality reduction method. However, 2DLDA may encounter the singularity issue theoretically and the sensitivity to outliers. In this paper, a generalized Lp-norm 2DLDA framework with regularization for an arbitrary $p>0$ is proposed, named G2DLDA. There are mainly two contributions of G2DLDA: one is G2DLDA model uses an arbitrary Lp-norm to measure the between-class and within-class scatter, and hence a proper $p$ can be selected to achieve the robustness. The other one is that by introducing an extra regularization term, G2DLDA achieves better generalization performance, and solves the singularity problem. In addition, G2DLDA can be solved through a series of convex problems with equality constraint, and it has closed solution for each single problem. Its convergence can be guaranteed theoretically when $1\leq p\leq2$. Preliminary experimental results on three contaminated human face databases show the effectiveness of the proposed G2DLDA.
Insensitive Stochastic Gradient Twin Support Vector Machine for Large Scale Problems
Nov 23, 2017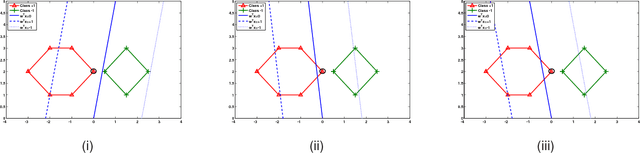
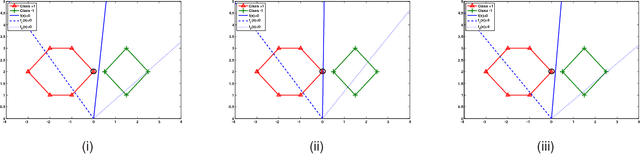

Abstract:Stochastic gradient descent algorithm has been successfully applied on support vector machines (called PEGASOS) for many classification problems. In this paper, stochastic gradient descent algorithm is investigated to twin support vector machines for classification. Compared with PEGASOS, the proposed stochastic gradient twin support vector machines (SGTSVM) is insensitive on stochastic sampling for stochastic gradient descent algorithm. In theory, we prove the convergence of SGTSVM instead of almost sure convergence of PEGASOS. For uniformly sampling, the approximation between SGTSVM and twin support vector machines is also given, while PEGASOS only has an opportunity to obtain an approximation of support vector machines. In addition, the nonlinear SGTSVM is derived directly from its linear case. Experimental results on both artificial datasets and large scale problems show the stable performance of SGTSVM with a fast learning speed.
* 31 pages, 31 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge