Pitch Preservation In Singing Voice Synthesis

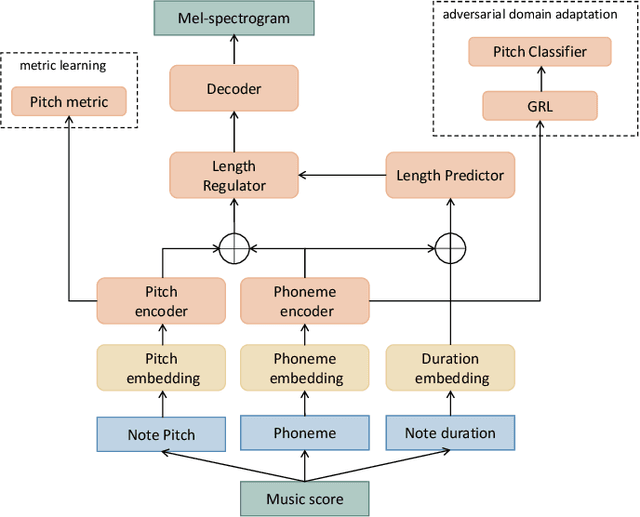
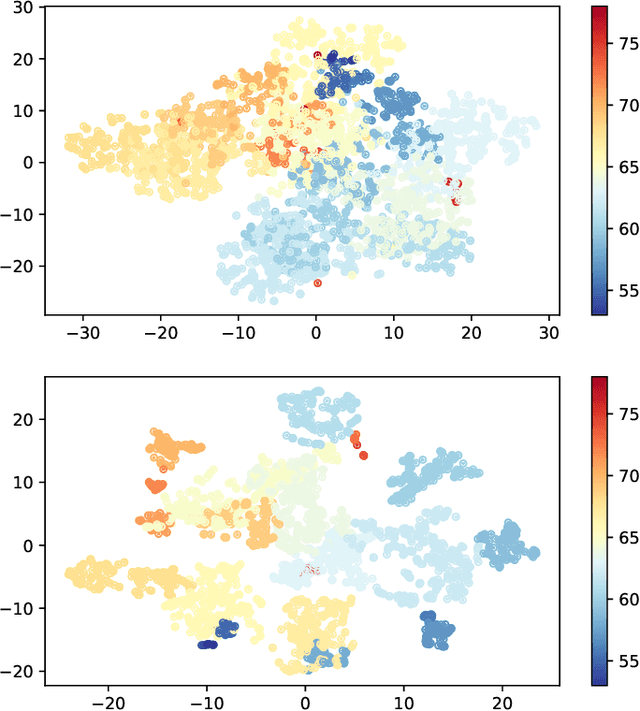
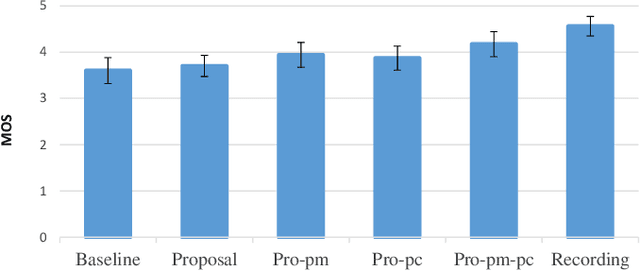
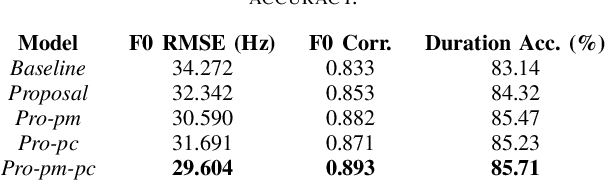
Suffering from limited singing voice corpus, existing singing voice synthesis (SVS) methods that build encoder-decoder neural networks to directly generate spectrogram could lead to out-of-tune issues during the inference phase. To attenuate these issues, this paper presents a novel acoustic model with independent pitch encoder and phoneme encoder, which disentangles the phoneme and pitch information from music score to fully utilize the corpus. Specifically, according to equal temperament theory, the pitch encoder is constrained by a pitch metric loss that maps distances between adjacent input pitches into corresponding frequency multiples between the encoder outputs. For the phoneme encoder, based on the analysis that same phonemes corresponding to varying pitches can produce similar pronunciations, this encoder is followed by an adversarially trained pitch classifier to enforce the identical phonemes with different pitches mapping into the same phoneme feature space. By these means, the sparse phonemes and pitches in original input spaces can be transformed into more compact feature spaces respectively, where the same elements cluster closely and cooperate mutually to enhance synthesis quality. Then, the outputs of the two encoders are summed together to pass through the following decoder in the acoustic model. Experimental results indicate that the proposed approaches can characterize intrinsic structure between pitch inputs to obtain better pitch synthesis accuracy and achieve superior singing synthesis performance against the advanced baseline system.

Support Vector Machine Classifier via $L_{0/1}$ Soft-Margin Loss

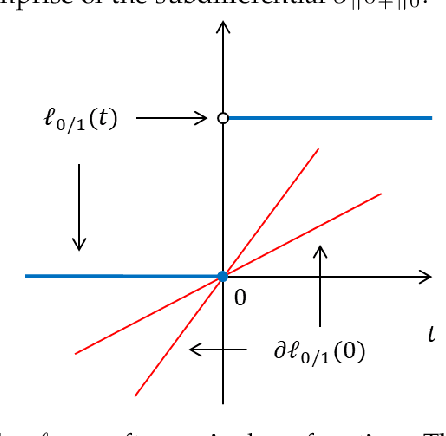
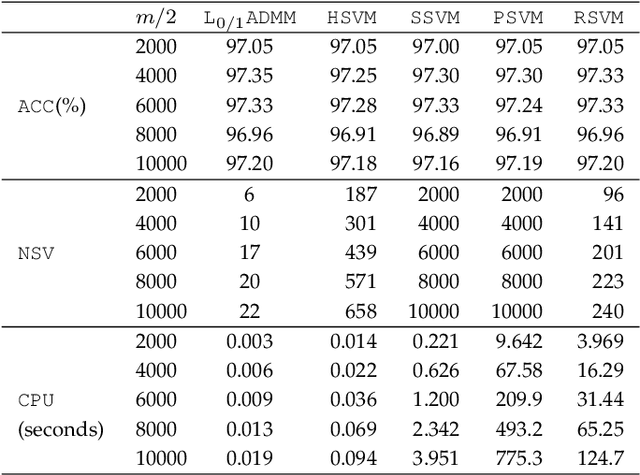
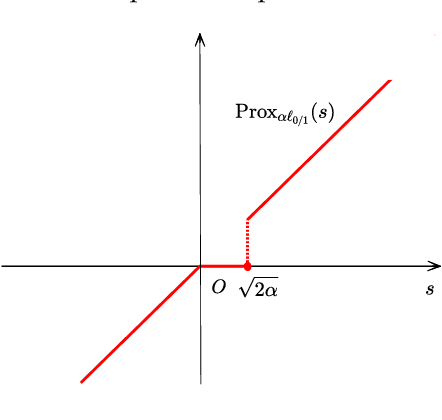
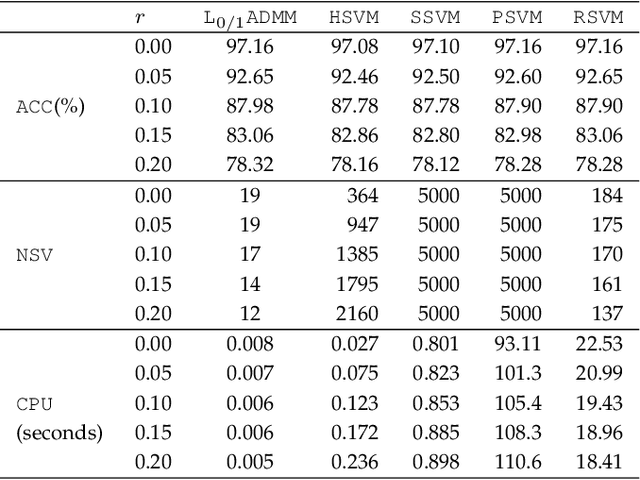
Support vector machine (SVM) has attracted great attentions for the last two decades due to its extensive applications, and thus numerous optimization models have been proposed. To distinguish all of them, in this paper, we introduce a new model equipped with an $L_{0/1}$ soft-margin loss (dubbed as $L_{0/1}$-SVM) which well captures the nature of the binary classification. Many of the existing convex/non-convex soft-margin losses can be viewed as a surrogate of the $L_{0/1}$ soft-margin loss. Despite the discrete nature of $L_{0/1}$, we manage to establish the existence of global minimizer of the new model as well as revealing the relationship among its minimizers and KKT/P-stationary points. These theoretical properties allow us to take advantage of the alternating direction method of multipliers. In addition, the $L_{0/1}$-support vector operator is introduced as a filter to prevent outliers from being support vectors during the training process. Hence, the method is expected to be relatively robust. Finally, numerical experiments demonstrate that our proposed method generates better performance in terms of much shorter computational time with much fewer number of support vectors when against with some other leading methods in areas of SVM. When the data size gets bigger, its advantage becomes more evident.

Single Versus Union: Non-parallel Support Vector Machine Frameworks

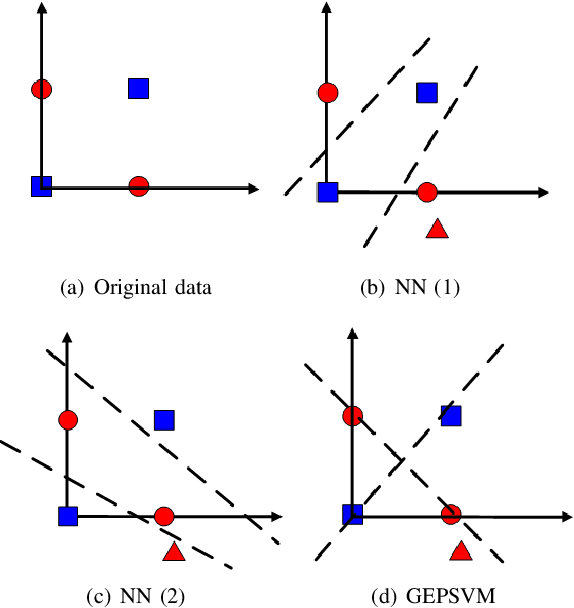
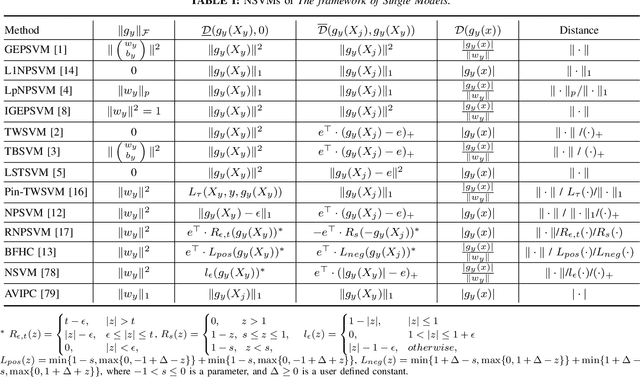
Considering the classification problem, we summarize the nonparallel support vector machines with the nonparallel hyperplanes to two types of frameworks. The first type constructs the hyperplanes separately. It solves a series of small optimization problems to obtain a series of hyperplanes, but is hard to measure the loss of each sample. The other type constructs all the hyperplanes simultaneously, and it solves one big optimization problem with the ascertained loss of each sample. We give the characteristics of each framework and compare them carefully. In addition, based on the second framework, we construct a max-min distance-based nonparallel support vector machine for multiclass classification problem, called NSVM. It constructs hyperplanes with large distance margin by solving an optimization problem. Experimental results on benchmark data sets and human face databases show the advantages of our NSVM.