Twin support vector quantile regression

We propose a twin support vector quantile regression (TSVQR) to capture the heterogeneous and asymmetric information in modern data. Using a quantile parameter, TSVQR effectively depicts the heterogeneous distribution information with respect to all portions of data points. Correspondingly, TSVQR constructs two smaller sized quadratic programming problems (QPPs) to generate two nonparallel planes to measure the distributional asymmetry between the lower and upper bounds at each quantile level. The QPPs in TSVQR are smaller and easier to solve than those in previous quantile regression methods. Moreover, the dual coordinate descent algorithm for TSVQR also accelerates the training speed. Experimental results on six artiffcial data sets, ffve benchmark data sets, two large scale data sets, two time-series data sets, and two imbalanced data sets indicate that the TSVQR outperforms previous quantile regression methods in terms of the effectiveness of completely capturing the heterogeneous and asymmetric information and the efffciency of the learning process.

CNTS: Cooperative Network for Time Series

The use of deep learning techniques in detecting anomalies in time series data has been an active area of research with a long history of development and a variety of approaches. In particular, reconstruction-based unsupervised anomaly detection methods have gained popularity due to their intuitive assumptions and low computational requirements. However, these methods are often susceptible to outliers and do not effectively model anomalies, leading to suboptimal results. This paper presents a novel approach for unsupervised anomaly detection, called the Cooperative Network Time Series (CNTS) approach. The CNTS system consists of two components: a detector and a reconstructor. The detector is responsible for directly detecting anomalies, while the reconstructor provides reconstruction information to the detector and updates its learning based on anomalous information received from the detector. The central aspect of CNTS is a multi-objective optimization problem, which is solved through a cooperative solution strategy. Experiments on three real-world datasets demonstrate the state-of-the-art performance of CNTS and confirm the cooperative effectiveness of the detector and reconstructor. The source code for this study is publicly available on GitHub.

Support Vector Machine Classifier via $L_{0/1}$ Soft-Margin Loss

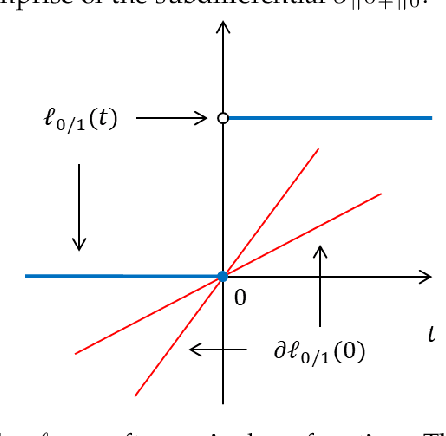
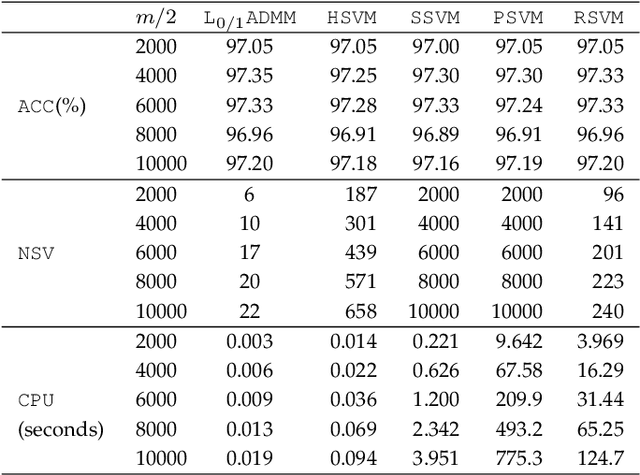
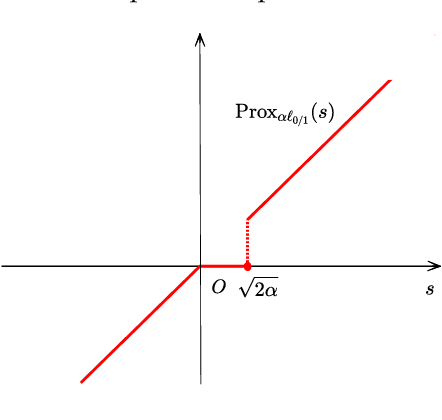
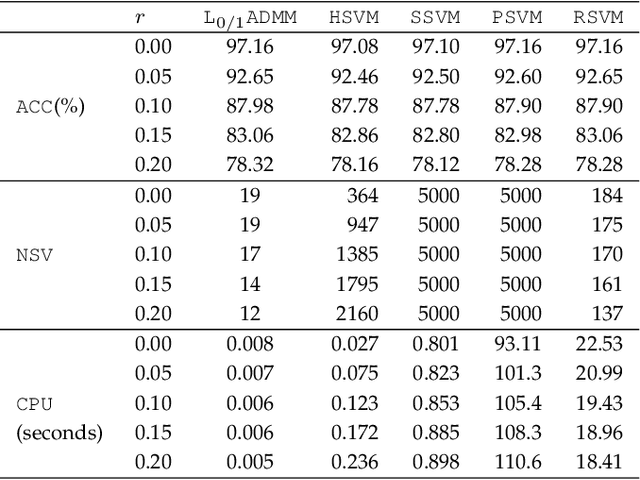
Support vector machine (SVM) has attracted great attentions for the last two decades due to its extensive applications, and thus numerous optimization models have been proposed. To distinguish all of them, in this paper, we introduce a new model equipped with an $L_{0/1}$ soft-margin loss (dubbed as $L_{0/1}$-SVM) which well captures the nature of the binary classification. Many of the existing convex/non-convex soft-margin losses can be viewed as a surrogate of the $L_{0/1}$ soft-margin loss. Despite the discrete nature of $L_{0/1}$, we manage to establish the existence of global minimizer of the new model as well as revealing the relationship among its minimizers and KKT/P-stationary points. These theoretical properties allow us to take advantage of the alternating direction method of multipliers. In addition, the $L_{0/1}$-support vector operator is introduced as a filter to prevent outliers from being support vectors during the training process. Hence, the method is expected to be relatively robust. Finally, numerical experiments demonstrate that our proposed method generates better performance in terms of much shorter computational time with much fewer number of support vectors when against with some other leading methods in areas of SVM. When the data size gets bigger, its advantage becomes more evident.