Support Vector Machine Classifier via $L_{0/1}$ Soft-Margin Loss
Paper and Code
Dec 16, 2019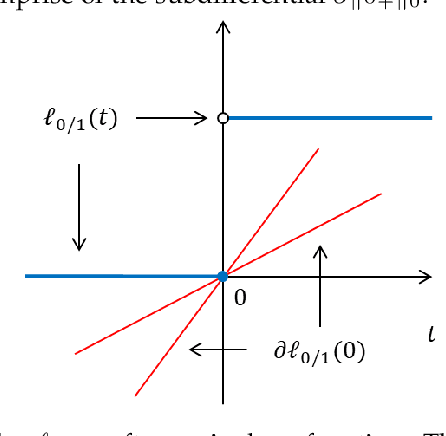
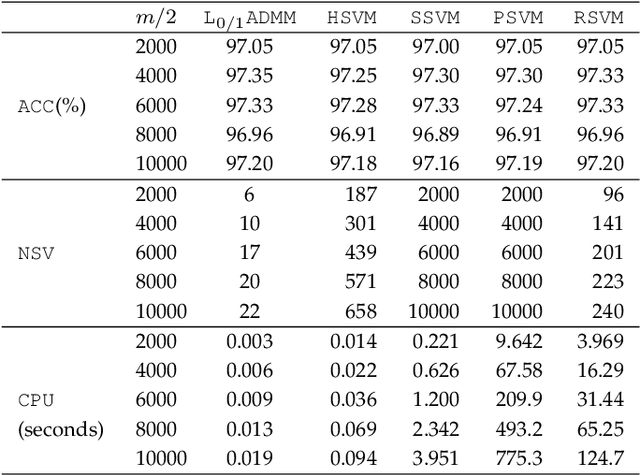
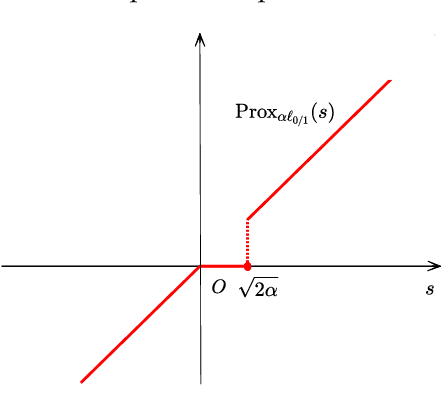
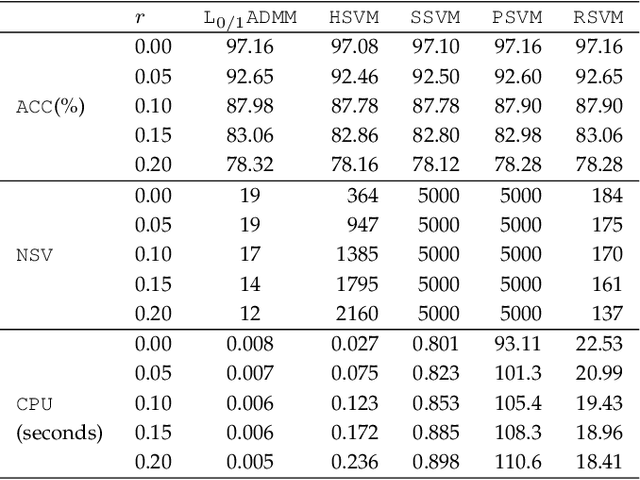
Support vector machine (SVM) has attracted great attentions for the last two decades due to its extensive applications, and thus numerous optimization models have been proposed. To distinguish all of them, in this paper, we introduce a new model equipped with an $L_{0/1}$ soft-margin loss (dubbed as $L_{0/1}$-SVM) which well captures the nature of the binary classification. Many of the existing convex/non-convex soft-margin losses can be viewed as a surrogate of the $L_{0/1}$ soft-margin loss. Despite the discrete nature of $L_{0/1}$, we manage to establish the existence of global minimizer of the new model as well as revealing the relationship among its minimizers and KKT/P-stationary points. These theoretical properties allow us to take advantage of the alternating direction method of multipliers. In addition, the $L_{0/1}$-support vector operator is introduced as a filter to prevent outliers from being support vectors during the training process. Hence, the method is expected to be relatively robust. Finally, numerical experiments demonstrate that our proposed method generates better performance in terms of much shorter computational time with much fewer number of support vectors when against with some other leading methods in areas of SVM. When the data size gets bigger, its advantage becomes more evident.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge