Multiple Flat Projections for Cross-manifold Clustering
Paper and Code
Feb 17, 2020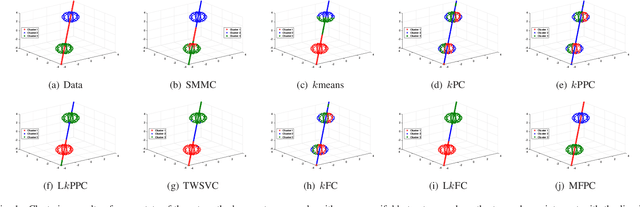

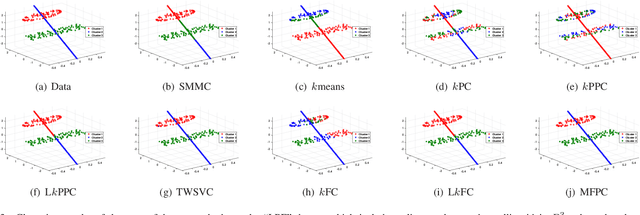
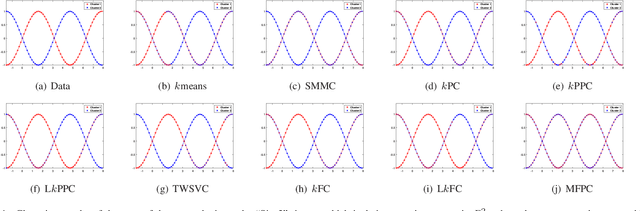
Cross-manifold clustering is a hard topic and many traditional clustering methods fail because of the cross-manifold structures. In this paper, we propose a Multiple Flat Projections Clustering (MFPC) to deal with cross-manifold clustering problems. In our MFPC, the given samples are projected into multiple subspaces to discover the global structures of the implicit manifolds. Thus, the cross-manifold clusters are distinguished from the various projections. Further, our MFPC is extended to nonlinear manifold clustering via kernel tricks to deal with more complex cross-manifold clustering. A series of non-convex matrix optimization problems in MFPC are solved by a proposed recursive algorithm. The synthetic tests show that our MFPC works on the cross-manifold structures well. Moreover, experimental results on the benchmark datasets show the excellent performance of our MFPC compared with some state-of-the-art clustering methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge