Fuzzy Discriminant Clustering with Fuzzy Pairwise Constraints

In semi-supervised fuzzy clustering, this paper extends the traditional pairwise constraint (i.e., must-link or cannot-link) to fuzzy pairwise constraint. The fuzzy pairwise constraint allows a supervisor to provide the grade of similarity or dissimilarity between the implicit fuzzy vectors of a pair of samples. This constraint can present more complicated relationship between the pair of samples and avoid eliminating the fuzzy characteristics. We propose a fuzzy discriminant clustering model (FDC) to fuse the fuzzy pairwise constraints. The nonconvex optimization problem in our FDC is solved by a modified expectation-maximization algorithm, involving to solve several indefinite quadratic programming problems (IQPPs). Further, a diagonal block coordinate decent (DBCD) algorithm is proposed for these IQPPs, whose stationary points are guaranteed, and the global solutions can be obtained under certain conditions. To suit for different applications, the FDC is extended into various metric spaces, e.g., the Reproducing Kernel Hilbert Space. Experimental results on several benchmark datasets and facial expression database demonstrate the outperformance of our FDC compared with some state-of-the-art clustering models.

Two-dimensional Bhattacharyya bound linear discriminant analysis with its applications

Recently proposed L2-norm linear discriminant analysis criterion via the Bhattacharyya error bound estimation (L2BLDA) is an effective improvement of linear discriminant analysis (LDA) for feature extraction. However, L2BLDA is only proposed to cope with vector input samples. When facing with two-dimensional (2D) inputs, such as images, it will lose some useful information, since it does not consider intrinsic structure of images. In this paper, we extend L2BLDA to a two-dimensional Bhattacharyya bound linear discriminant analysis (2DBLDA). 2DBLDA maximizes the matrix-based between-class distance which is measured by the weighted pairwise distances of class means and meanwhile minimizes the matrix-based within-class distance. The weighting constant between the between-class and within-class terms is determined by the involved data that makes the proposed 2DBLDA adaptive. In addition, the criterion of 2DBLDA is equivalent to optimizing an upper bound of the Bhattacharyya error. The construction of 2DBLDA makes it avoid the small sample size problem while also possess robustness, and can be solved through a simple standard eigenvalue decomposition problem. The experimental results on image recognition and face image reconstruction demonstrate the effectiveness of the proposed methods.

Multiple Flat Projections for Cross-manifold Clustering

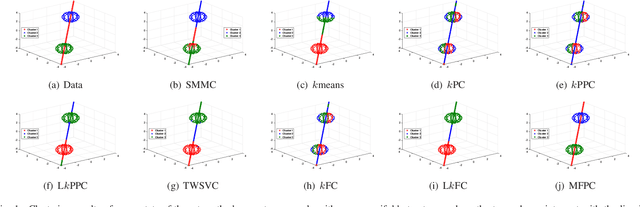
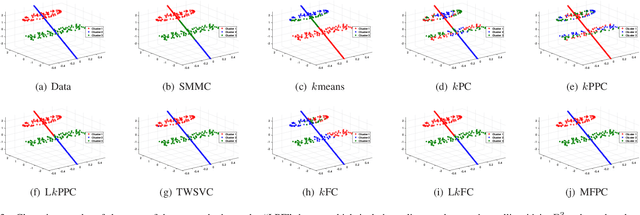
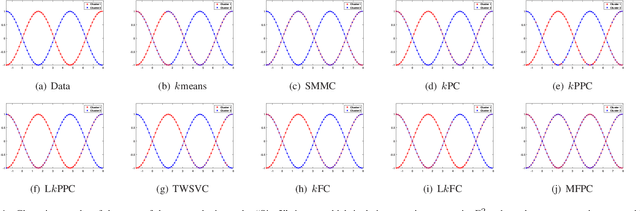
Cross-manifold clustering is a hard topic and many traditional clustering methods fail because of the cross-manifold structures. In this paper, we propose a Multiple Flat Projections Clustering (MFPC) to deal with cross-manifold clustering problems. In our MFPC, the given samples are projected into multiple subspaces to discover the global structures of the implicit manifolds. Thus, the cross-manifold clusters are distinguished from the various projections. Further, our MFPC is extended to nonlinear manifold clustering via kernel tricks to deal with more complex cross-manifold clustering. A series of non-convex matrix optimization problems in MFPC are solved by a proposed recursive algorithm. The synthetic tests show that our MFPC works on the cross-manifold structures well. Moreover, experimental results on the benchmark datasets show the excellent performance of our MFPC compared with some state-of-the-art clustering methods.

A general model for plane-based clustering with loss function

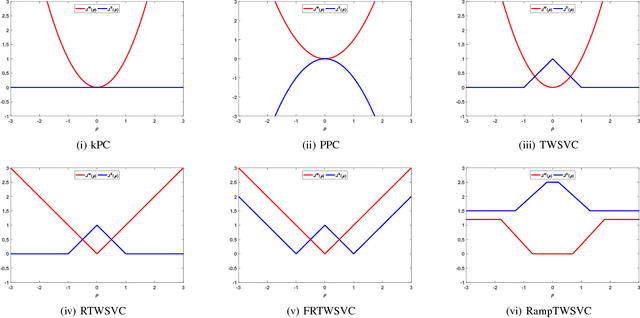
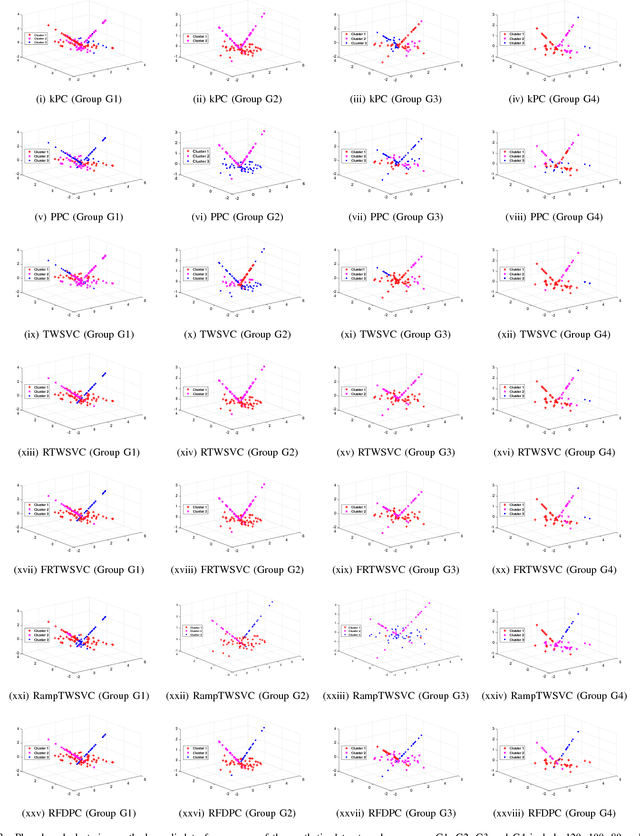
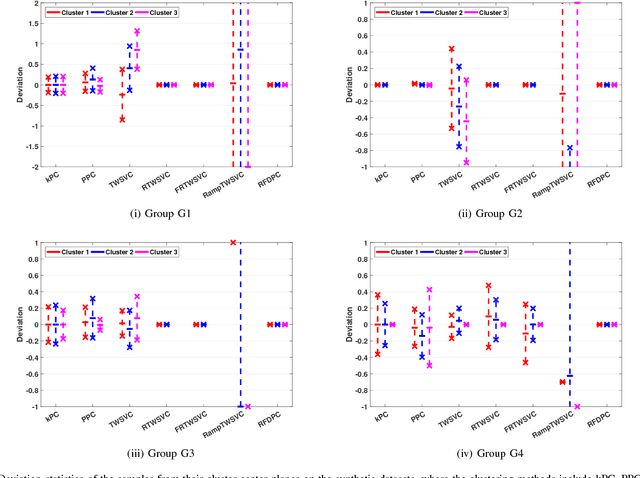
In this paper, we propose a general model for plane-based clustering. The general model contains many existing plane-based clustering methods, e.g., k-plane clustering (kPC), proximal plane clustering (PPC), twin support vector clustering (TWSVC) and its extensions. Under this general model, one may obtain an appropriate clustering method for specific purpose. The general model is a procedure corresponding to an optimization problem, where the optimization problem minimizes the total loss of the samples. Thereinto, the loss of a sample derives from both within-cluster and between-cluster. In theory, the termination conditions are discussed, and we prove that the general model terminates in a finite number of steps at a local or weak local optimal point. Furthermore, based on this general model, we propose a plane-based clustering method by introducing a new loss function to capture the data distribution precisely. Experimental results on artificial and public available datasets verify the effectiveness of the proposed method.

Insensitive Stochastic Gradient Twin Support Vector Machine for Large Scale Problems

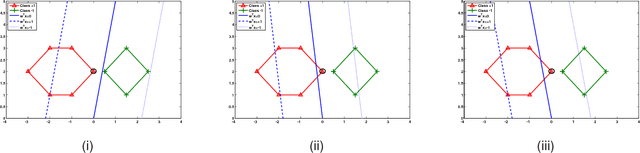
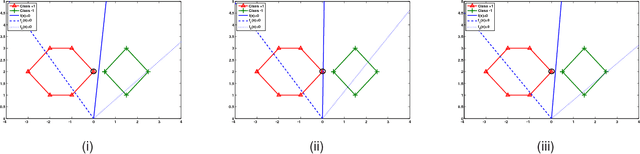
Stochastic gradient descent algorithm has been successfully applied on support vector machines (called PEGASOS) for many classification problems. In this paper, stochastic gradient descent algorithm is investigated to twin support vector machines for classification. Compared with PEGASOS, the proposed stochastic gradient twin support vector machines (SGTSVM) is insensitive on stochastic sampling for stochastic gradient descent algorithm. In theory, we prove the convergence of SGTSVM instead of almost sure convergence of PEGASOS. For uniformly sampling, the approximation between SGTSVM and twin support vector machines is also given, while PEGASOS only has an opportunity to obtain an approximation of support vector machines. In addition, the nonlinear SGTSVM is derived directly from its linear case. Experimental results on both artificial datasets and large scale problems show the stable performance of SGTSVM with a fast learning speed.