SA-DVAE: Improving Zero-Shot Skeleton-Based Action Recognition by Disentangled Variational Autoencoders

Existing zero-shot skeleton-based action recognition methods utilize projection networks to learn a shared latent space of skeleton features and semantic embeddings. The inherent imbalance in action recognition datasets, characterized by variable skeleton sequences yet constant class labels, presents significant challenges for alignment. To address the imbalance, we propose SA-DVAE -- Semantic Alignment via Disentangled Variational Autoencoders, a method that first adopts feature disentanglement to separate skeleton features into two independent parts -- one is semantic-related and another is irrelevant -- to better align skeleton and semantic features. We implement this idea via a pair of modality-specific variational autoencoders coupled with a total correction penalty. We conduct experiments on three benchmark datasets: NTU RGB+D, NTU RGB+D 120 and PKU-MMD, and our experimental results show that SA-DAVE produces improved performance over existing methods. The code is available at https://github.com/pha123661/SA-DVAE.

Nonlinear Kernel Support Vector Machine with 0-1 Soft Margin Loss

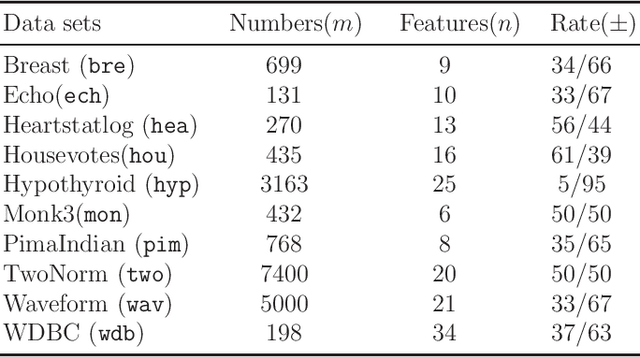
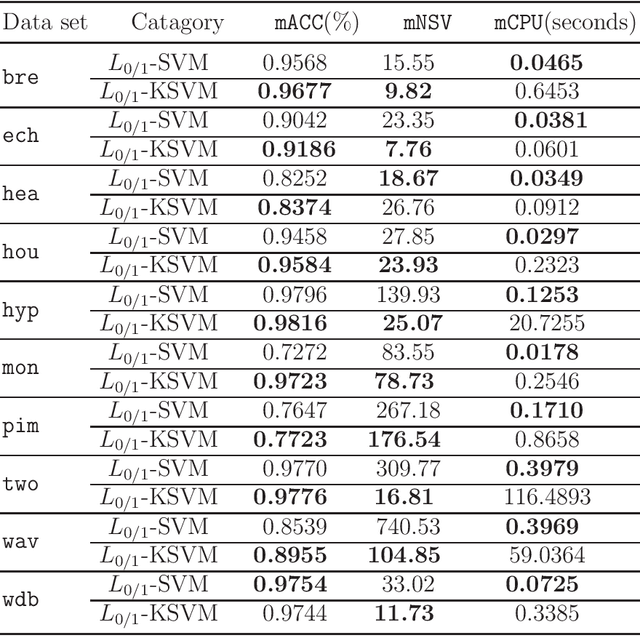
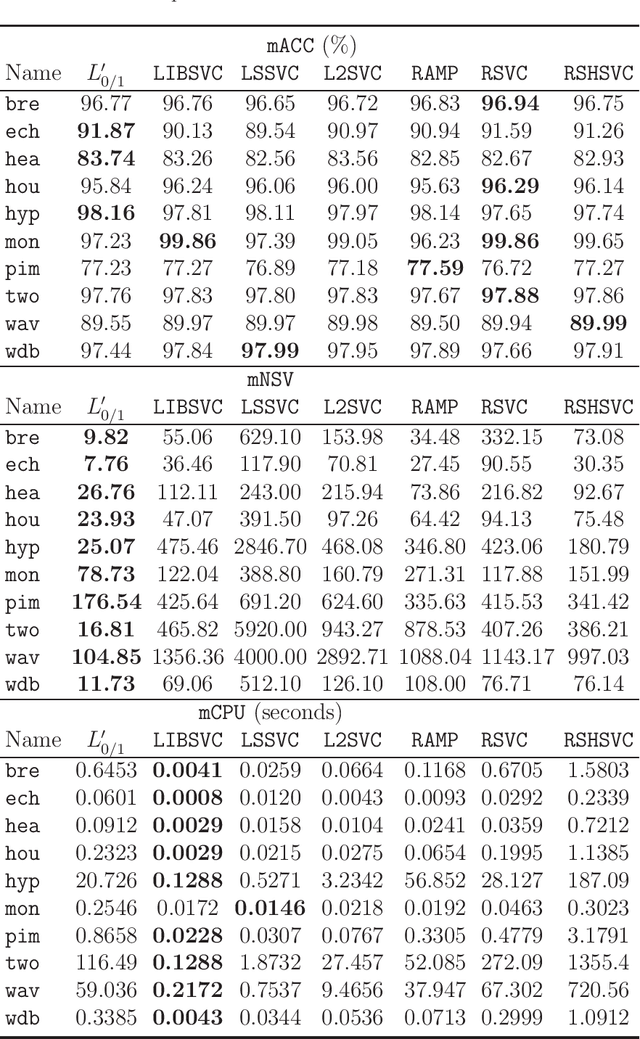
Recent advance on linear support vector machine with the 0-1 soft margin loss ($L_{0/1}$-SVM) shows that the 0-1 loss problem can be solved directly. However, its theoretical and algorithmic requirements restrict us extending the linear solving framework to its nonlinear kernel form directly, the absence of explicit expression of Lagrangian dual function of $L_{0/1}$-SVM is one big deficiency among of them. In this paper, by applying the nonparametric representation theorem, we propose a nonlinear model for support vector machine with 0-1 soft margin loss, called $L_{0/1}$-KSVM, which cunningly involves the kernel technique into it and more importantly, follows the success on systematically solving its linear task. Its optimal condition is explored theoretically and a working set selection alternating direction method of multipliers (ADMM) algorithm is introduced to acquire its numerical solution. Moreover, we firstly present a closed-form definition to the support vector (SV) of $L_{0/1}$-KSVM. Theoretically, we prove that all SVs of $L_{0/1}$-KSVM are only located on the parallel decision surfaces. The experiment part also shows that $L_{0/1}$-KSVM has much fewer SVs, simultaneously with a decent predicting accuracy, when comparing to its linear peer $L_{0/1}$-SVM and the other six nonlinear benchmark SVM classifiers.

Multiple Flat Projections for Cross-manifold Clustering

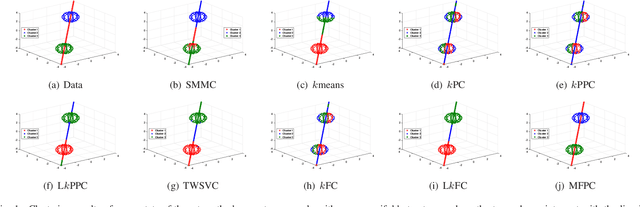
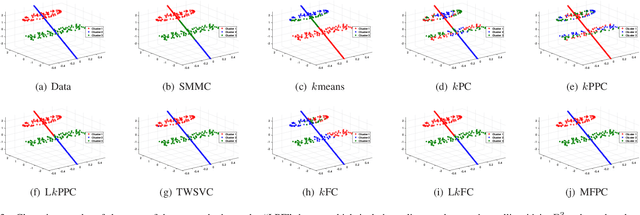
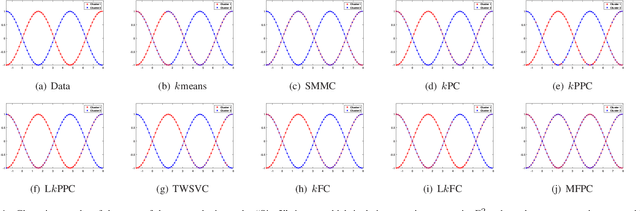
Cross-manifold clustering is a hard topic and many traditional clustering methods fail because of the cross-manifold structures. In this paper, we propose a Multiple Flat Projections Clustering (MFPC) to deal with cross-manifold clustering problems. In our MFPC, the given samples are projected into multiple subspaces to discover the global structures of the implicit manifolds. Thus, the cross-manifold clusters are distinguished from the various projections. Further, our MFPC is extended to nonlinear manifold clustering via kernel tricks to deal with more complex cross-manifold clustering. A series of non-convex matrix optimization problems in MFPC are solved by a proposed recursive algorithm. The synthetic tests show that our MFPC works on the cross-manifold structures well. Moreover, experimental results on the benchmark datasets show the excellent performance of our MFPC compared with some state-of-the-art clustering methods.

Generalized two-dimensional linear discriminant analysis with regularization

Recent advances show that two-dimensional linear discriminant analysis (2DLDA) is a successful matrix based dimensionality reduction method. However, 2DLDA may encounter the singularity issue theoretically and the sensitivity to outliers. In this paper, a generalized Lp-norm 2DLDA framework with regularization for an arbitrary $p>0$ is proposed, named G2DLDA. There are mainly two contributions of G2DLDA: one is G2DLDA model uses an arbitrary Lp-norm to measure the between-class and within-class scatter, and hence a proper $p$ can be selected to achieve the robustness. The other one is that by introducing an extra regularization term, G2DLDA achieves better generalization performance, and solves the singularity problem. In addition, G2DLDA can be solved through a series of convex problems with equality constraint, and it has closed solution for each single problem. Its convergence can be guaranteed theoretically when $1\leq p\leq2$. Preliminary experimental results on three contaminated human face databases show the effectiveness of the proposed G2DLDA.