Principal Component Analysis Based on T$\ell_1$-norm Maximization

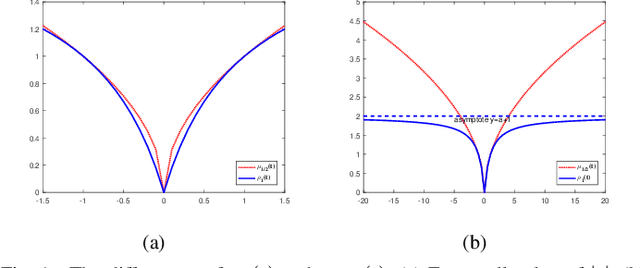
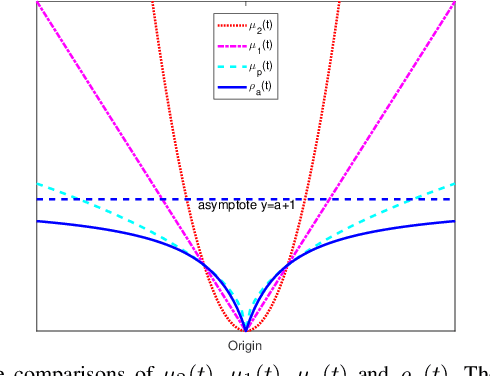
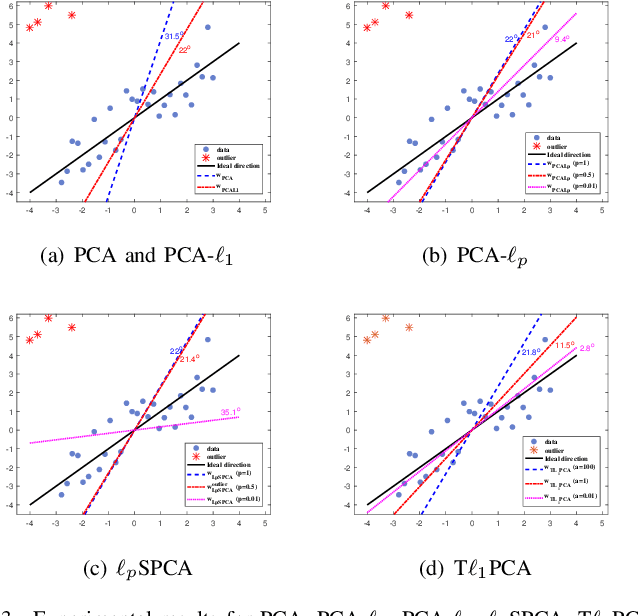
Classical principal component analysis (PCA) may suffer from the sensitivity to outliers and noise. Therefore PCA based on $\ell_1$-norm and $\ell_p$-norm ($0 < p < 1$) have been studied. Among them, the ones based on $\ell_p$-norm seem to be most interesting from the robustness point of view. However, their numerical performance is not satisfactory. Note that, although T$\ell_1$-norm is similar to $\ell_p$-norm ($0 < p < 1$) in some sense, it has the stronger suppression effect to outliers and better continuity. So PCA based on T$\ell_1$-norm is proposed in this paper. Our numerical experiments have shown that its performance is superior than PCA-$\ell_p$ and $\ell_p$SPCA as well as PCA, PCA-$\ell_1$ obviously.

A general model for plane-based clustering with loss function

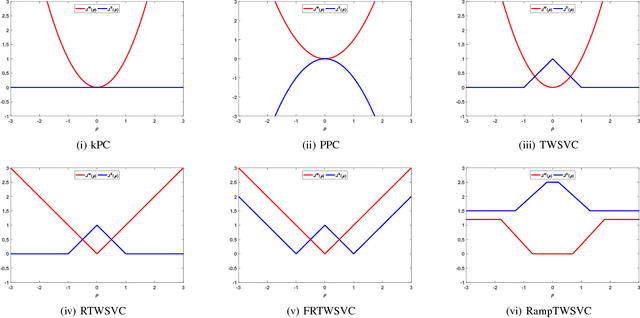
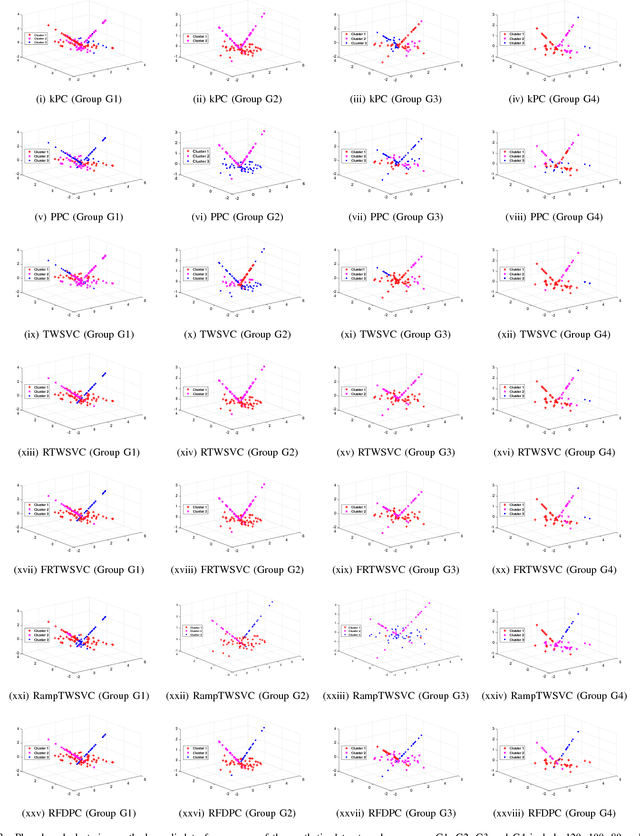
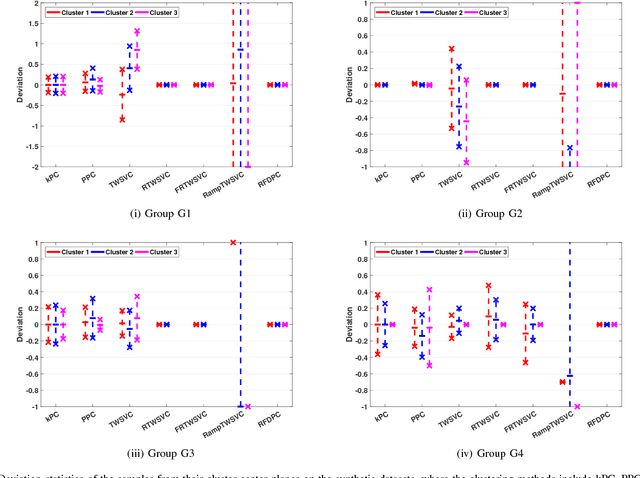
In this paper, we propose a general model for plane-based clustering. The general model contains many existing plane-based clustering methods, e.g., k-plane clustering (kPC), proximal plane clustering (PPC), twin support vector clustering (TWSVC) and its extensions. Under this general model, one may obtain an appropriate clustering method for specific purpose. The general model is a procedure corresponding to an optimization problem, where the optimization problem minimizes the total loss of the samples. Thereinto, the loss of a sample derives from both within-cluster and between-cluster. In theory, the termination conditions are discussed, and we prove that the general model terminates in a finite number of steps at a local or weak local optimal point. Furthermore, based on this general model, we propose a plane-based clustering method by introducing a new loss function to capture the data distribution precisely. Experimental results on artificial and public available datasets verify the effectiveness of the proposed method.

Insensitive Stochastic Gradient Twin Support Vector Machine for Large Scale Problems

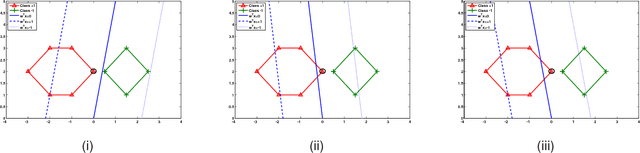
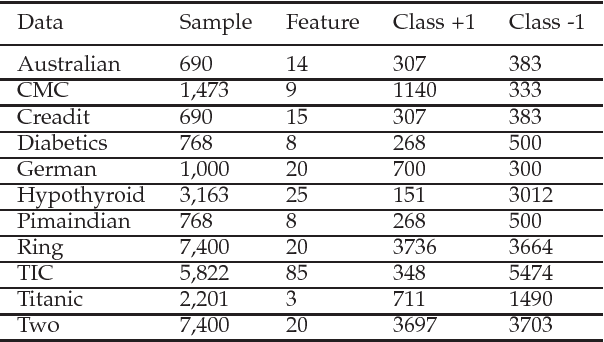
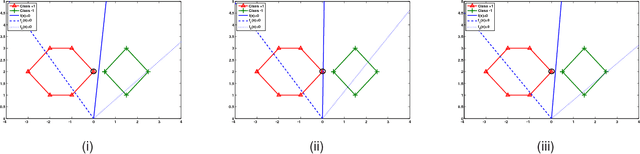
Stochastic gradient descent algorithm has been successfully applied on support vector machines (called PEGASOS) for many classification problems. In this paper, stochastic gradient descent algorithm is investigated to twin support vector machines for classification. Compared with PEGASOS, the proposed stochastic gradient twin support vector machines (SGTSVM) is insensitive on stochastic sampling for stochastic gradient descent algorithm. In theory, we prove the convergence of SGTSVM instead of almost sure convergence of PEGASOS. For uniformly sampling, the approximation between SGTSVM and twin support vector machines is also given, while PEGASOS only has an opportunity to obtain an approximation of support vector machines. In addition, the nonlinear SGTSVM is derived directly from its linear case. Experimental results on both artificial datasets and large scale problems show the stable performance of SGTSVM with a fast learning speed.