Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Xiang-Fei Yang
Principal Component Analysis Based on T$\ell_1$-norm Maximization
May 23, 2020Figures and Tables: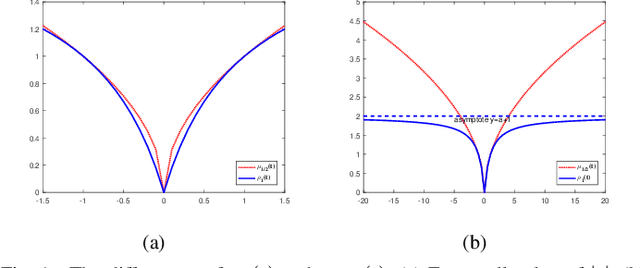
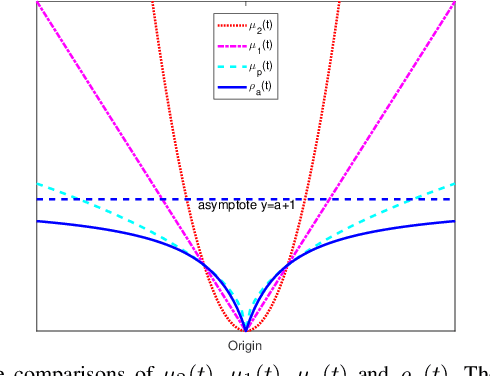
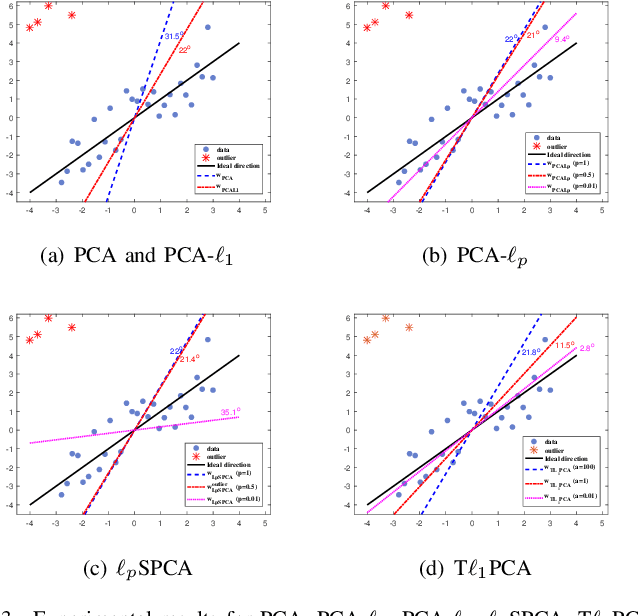





Abstract:Classical principal component analysis (PCA) may suffer from the sensitivity to outliers and noise. Therefore PCA based on $\ell_1$-norm and $\ell_p$-norm ($0 < p < 1$) have been studied. Among them, the ones based on $\ell_p$-norm seem to be most interesting from the robustness point of view. However, their numerical performance is not satisfactory. Note that, although T$\ell_1$-norm is similar to $\ell_p$-norm ($0 < p < 1$) in some sense, it has the stronger suppression effect to outliers and better continuity. So PCA based on T$\ell_1$-norm is proposed in this paper. Our numerical experiments have shown that its performance is superior than PCA-$\ell_p$ and $\ell_p$SPCA as well as PCA, PCA-$\ell_1$ obviously.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge