A general model for plane-based clustering with loss function
Paper and Code
Jan 26, 2019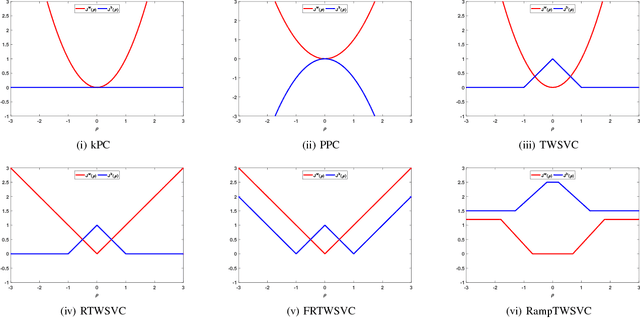

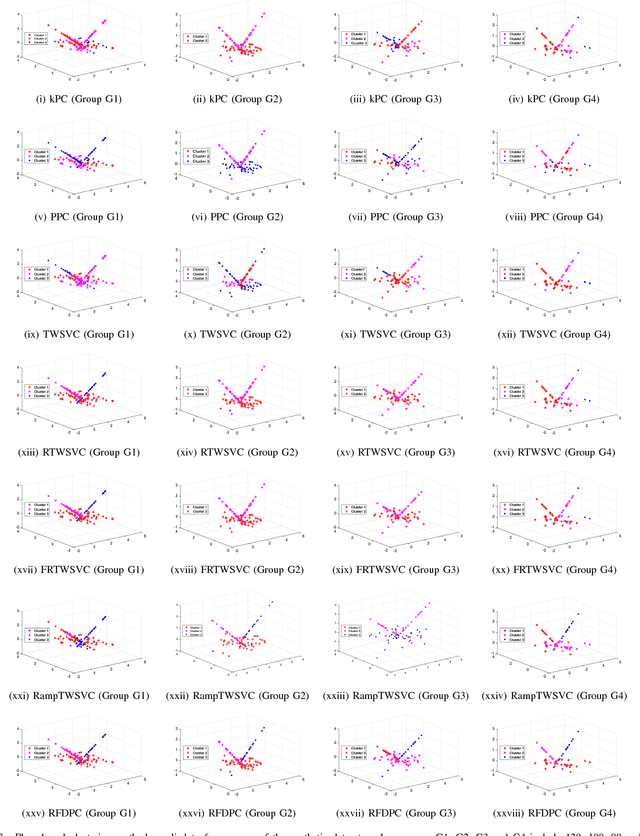
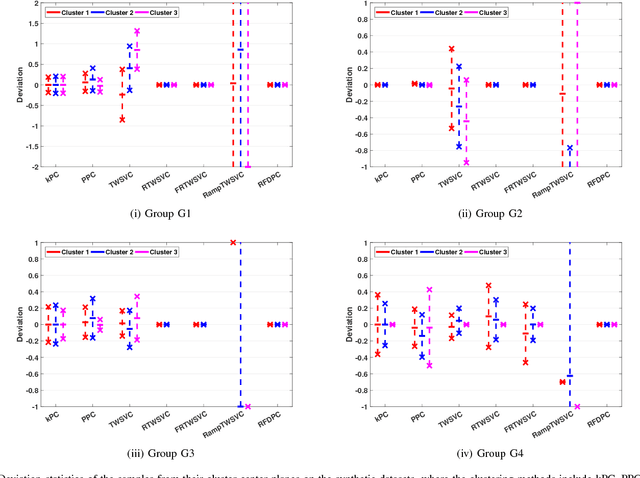
In this paper, we propose a general model for plane-based clustering. The general model contains many existing plane-based clustering methods, e.g., k-plane clustering (kPC), proximal plane clustering (PPC), twin support vector clustering (TWSVC) and its extensions. Under this general model, one may obtain an appropriate clustering method for specific purpose. The general model is a procedure corresponding to an optimization problem, where the optimization problem minimizes the total loss of the samples. Thereinto, the loss of a sample derives from both within-cluster and between-cluster. In theory, the termination conditions are discussed, and we prove that the general model terminates in a finite number of steps at a local or weak local optimal point. Furthermore, based on this general model, we propose a plane-based clustering method by introducing a new loss function to capture the data distribution precisely. Experimental results on artificial and public available datasets verify the effectiveness of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge